Геометричний метод розв’язування ЗЛП

Для ЗЛП з двома невідомими процес вибору оптимального плану з кутових точок області допустимих розв’язків можна проводити за допомогою графічного зображення цієї області. Для цього в декартовій системі координат креслимо многокутник розв’язків системи обмежень (як перетин множин розв’язків кожної нерівності системи), а потім, враховуючи напрямок зростання цільової функції, обираємо оптимальну вершину цього многокутника і знаходимо її координати. Розглянемо докладніше процес побудови області допустимих розв’язків.

Як відомо, графічним зображенням множини розв’язків лінійного рівняння з двома невідомими є пряма на координатній площині. Геометричним місцем точок з координатами, що задовольняють лінійну нерівність, є одна з двох напівплощин, на які поділяє площину пряма з відповідним рівнянням. Для визначення, яку саме напівплощину треба обрати, достатньо перевірити виконання нерівності в одній з точок площини. Наприклад, побудуємо графічний розв’язок нерівності 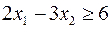(рис. 1). Розглянемо рівняння 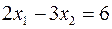і побудуємо пряму, яка є множиною його розв’язків на площині .

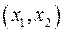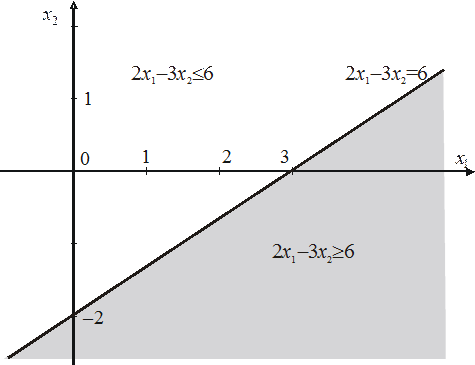
Рис. 1. Графічний розв’язок лінійної нерівності.

Ця пряма поділяє площину на дві напівплощини. Перевіримо виконання нерівності у початку координат. Для цього підставимо у нерівність 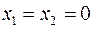. Отримаємо 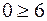, що не є вірною нерівністю. Тому у початку координат нерівність не виконується, і також вона не виконується у всіх точках тієї напівплощини, до якої належить початок координат. Тому шуканий розв’язок нерівності – це напівплощина, що лежить нижче від прямої. На рисунку це затонована напівплощина. Інша напівплощина є розв’язком нерівності .

Якщо задана система нерівностей, то для її розв’язання треба на одній координатній площині побудувати графічний розв’язок кожної нерівності і знайти перетин отриманих напівплощин. Наприклад, розв’язком системи

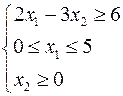
є трикутник, що залишився незаштрихованим на рисунку 2.

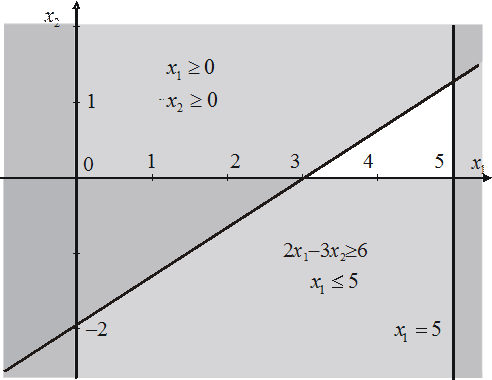
Рис. 2. Графічний розв’язок системи лінійних нерівностейі.

Розглянемо тепер поведінку цільової функції у точках площини. Лінією рівня (тобто лінією, на якій функція зберігає стале значення) лінійної цільової функції є пряма. Сімейство таких прямих має спільний вектор нормалі 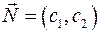, тобто усі прямі сімейства є паралельними одна одній. Якщо така пряма проходить через початок координат, то значення цільової функції в її точках дорівнює 0. Напрямок зростання значень цільової функції теж визначається напрямком вектора 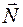(рис. 3). Таким чином, для знаходження найбільшого значення цільової функції в області припустимих розв’язків треба побудувати таку пряму, яка має заданий вектор нормалі 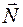, проходить через область припустимих розв’язків та розташована якомога далі у напрямку вектора 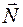. При знаходженні найменшого значення функції треба обирати пряму, яка розташована якомога далі у напрямку, протилежному вектору .

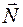Рис. 3. Лінії рівня цільової функції.

Приклад 2.

Розв’яжемо геометричним методом задачу про використання сировини, яка задана формулами (6), (7) (рис. 4). Областю допустимих розв’язків цієї задачі є шестикутник . Лінії рівня цільової функції перпендикулярні вектору 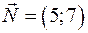. Якщо зсувати, наприклад, пряму 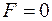у напрямку вектора 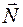, значення функції зростатиме. Максимально можливий зсув досягається у вершині 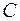, тобто 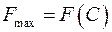. Координати точки 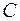знаходимо як координати точки перетину двох прямих, розв’язуючи систему рівнянь

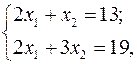
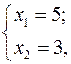
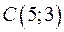Підставивши до цільової функції координати знайденої точки, знаходимо .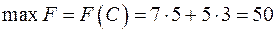

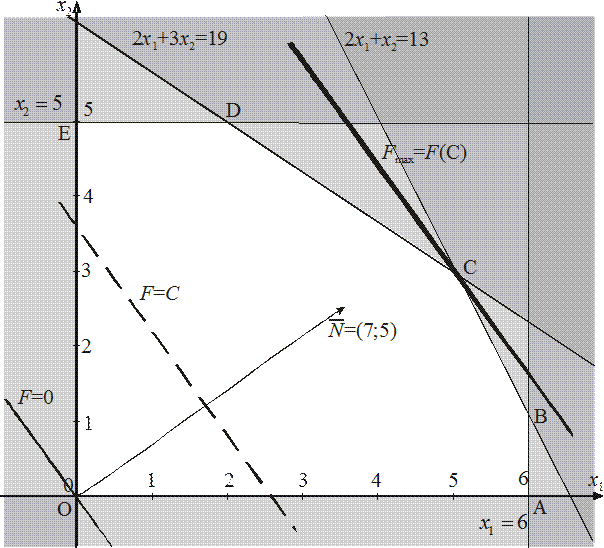
Рис. 4. Приклад геометричного розв’язання ЗЛП.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Математична модель задачі про використання сировини.	\|	Зведення ЗЛП до канонічної форми

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.013 сек.