• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Поняття простого та складного процентів, як основи процесів нарощування та дисконтування

У практиці інвестиційного аналізу «темп приросту» грошових засобів прийнято називати відсотком, ставкою відсотка або нормо рентабельності. Процес, в якому при заданих величинах первинної суми і темпу її зростання необхідно знайти майбутню вартість інвестованих засобів, називається процесом наращувания. Економічний сенс операції нарощування — поетапне збільшення первинної суми (наприклад, вкладу) шляхом приєднання до неї процентних платежів.

При проведені фінансово-економічних розрахунків, пов’язаних з інвестуванням коштів, процеси нарощування вартості можуть здійснюватися як за простими, так і за складними процентами.

Процент – сума доходу від наданого капіталу або плата за користування позичковим капіталом у всіх його формах.

Простий процент – сума доходу (додаткового грошового потоку), яка нараховується за основною сумою капіталу в кожному інтервалі часу і виплачується.

Складний процент – сума доходу (додаткового грошового потоку), яка нараховується за основною сумою капіталу за визначений період часу , яка не виплачується, а додається до основної суми капіталу.

I = PV i t, де (4.1)

I – величина прибутку власника інвестицій,

і – процентна ставка, (interest)

t – період часу інвестування, (time)

PV – первісна (теперішня) сума інвестицій (вкладу). (present value)

Суть методу нарахування за простими процентами зводиться до того, що проценти нараховують впродовж усього терміну інвестицій (кредиту) на ту саму величину капіталу, що інвестується. Наприкінці періоду t сума, одержувана інвестором дорівнює PV + I. Тоді:

FV = PV + I = PV + PVit = PV (1 + it),(4.2)

де FV – майбутня вартість грошових потоків, (future value)

РV – теперішня (первісна) вартість грошових потоків,

I – величина прибутку власника інвестицій,

і – процентна ставка,

t – період часу інвестування.

Величина (1 + it) зветься множником нарощування простих процентів.

Метод нарахування по складних процентах полягає в тому, що в першому періоді нарахування здійснюється на первісну суму інвестицій (кредиту), після цього вона складається з нарахованим процентом і в кожному наступному періоді проценти нараховуються на вже нарощену суму:

при t = n ,(4.3)

де 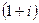- складний процент,

- множник нарощування складних процентів.

Читайте також:

1. CMM. Групи ключових процесів
2. CMM: зрілість організацій і процесів
3. I. Фізичні основи механіки
4. II. Поняття соціального процесу.
5. R – розрахунковий опір грунту основи, це такий тиск, при якому глибина зон пластичних деформацій (t) рівна 1/4b.
6. V. Поняття та ознаки (характеристики) злочинності
7. VII. Поняття про рану, рановий процес, види загоювання ран
8. VІII. Основи молекулярної фізики і термодинаміки
9. А/. Поняття про судовий процес.
10. Автоматизація виробничих процесів
11. АВТОМАТИЗАЦІЯ ТЕХНОЛОГІЧНИХ ПРОЦЕСІВ
12. АВТОМАТИЗАЦІЯ ТЕХНОЛОГІЧНИХ ПРОЦЕСІВ

Переглядів: 795