• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Рішення систем лінійних алгебраїчних рівнянь методом послідовного виключення невідомих. Метод Гауса.

Крамер

Нехай дано систему n-лін. рівнянь з 3n-невідомими

а11х1+а12х2=b1

а21х1+а22х2=b2 (1)

Домножимо 1р. на а22

2р-на (-а12)

3р-аn1

і складемо рівняння;після цьогоперше рівняння помножимо на а21,друге-на (-а11) і складемо одержані рівняння.Одержимо систему, еквівалентну системі (1) : (а11а22-а21а12)х1=в1а22-в2а12

(а11а22-а21а12)х2=в2а11-в1а21 (2)

систему (2) можна записати , використовуючи визначники

При розвязуванні системи можливі такі випадки:

1).∆≠0.Тоді система (3), а отже, і система (1) має один розвязок:

х1=∆1/∆, х2=∆2/∆

2).∆=0, ∆1≠0 або ∆2≠0 У цьому випадку система (1) несумісна.

3).∆=∆1=∆2=0 У цьому випадку система (1) складається з двох пропорційних рівнянь, тобто фактично зводиться до одного рівняння з двома невідомими, і тому має безліч розвязків :надаючи довільних значень одному невідомому, одержуватимемо значення іншого невідомого.

Рішення систем лінійних алгебраїчних рівнянь методом послідовного виключення невідомих. Метод Гауса.

Метод Гауса-це метод послідовного вилучення невідомих. За допомогою елементарних перетворень систему можна звести до рівносильної трапецієвидного або трикутного виду

Розглянемо систему 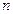лінійних алгебраїчних рівнянь відносно 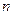невідомих Вважаємо, що серед коефіцієнтів 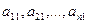при невідомому 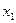є відмінні від нуля. Нехай таким буде 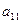. Тоді перше рівняння системи 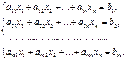(1)

почленно ділимо на і одержуємо

. (2)

Рівняння (2) множимо на і сумуємо з другим рівнянням системи (1); на 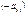і сумуємо з третім рівнянням; ..., на 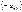і сумуємо з 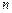-им рівнянням системи (1). Одержуємо систему, 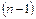-е рівняння якої не містить невідоме .

Аналогічно, послідовно вилучаючи 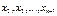, одержуємо систему, що має вигляд 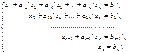. (3)

Поетапно піднімаючись знизу вгору в системі (3), знаходимо .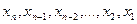

9.Рішення систем лінійних алгебраїчних рівнянь методом повного виключення невідомих. Метод Жордано Гауса.

МетодЖордано Гауса -це метод повного вилучення невідомих. На першому кроці ми виключаємо змінну 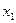з усіх рівнянь системи крім першого.На другому кроці виключаємо змінну 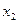з усіх рівнянь крім другого, на третьому кроці виключаємо змінну 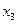з усіх рівнянь крім третього, на n-ому кроці змінна 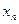виключається з усіх рівнянь крім n-ого рівняння.

Запишемо так звану розширену матрицю системи

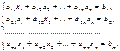(1)

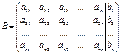. (2)

За допомогою еквівалентних перетворень: на першому кроці ми виключаємо змінну 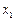з усіх рівнянь системи крім першого, на другому кроці виключаємо змінну 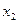з усіх рівнянь крім другого, на третьому кроці виключаємо змінну 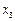з усіх рівнянь крім третього, на n-ому кроці змінна 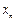виключається з усіх рівнянь крім n-ого рівняння. Матрицю (2) приводимо до вигляду

. (3)

Тоді з (3) знаходимо послідовно ,

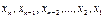Якщо за допомогою еквівалентних перетворень розширену матрицю В (2) системи (1) привести до вигляду

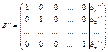, (4)

то отримаємо систему розв’язану методом Жордана-Гаусса.

10.Системма m-лінійних рівнянь з n-невідомими. Базисний мінор, базисні і вільні невідомі. Загальний і частинний розв’язок систем.

Розглянемо систему m лінійних алгебраїчних рівнянь відносно n невідомих:

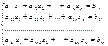(1)

Позначимо матрицю коефіцієнтів літерою А:

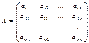. (2)

Розширену матрицю літерою В:

. (3)

Теорема

Якщо rang A=rang B, то система (1) сумісна. Якщо ця рівність не виконується, то система несумісна.

НАСЛІДОК

Якщо rang A=rang B=n, то система (1) має тільки один розв¢язок. Якщо ж rangA=rangB<n, то система (1) має нескінченну множину розв¢язків.

розглянемо випадок, коли система сумісна, але ранг менше кількості невідомих, тобто випадок, коли система має нескінченну множину розв¢язків.

Якщо ранг матриці коефіцієнтів дорівнює r, існує якийсь 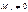. Він називається базисним мінором. Знайшовши цей базисний мінор, ми запишемо еквівалентну систему для системи (1). Для цього залишаємо тільки ті рівняння, коефіцієнти з яких утворили базисний мінор; при цьому члени рівнянь, коефіцієнти при яких не увійшли в базисний мінор, перенесемо вправо. Тоді одержимо систему r лінійних алгебраїчних рівнянь відносно r невідомих, а одержані праві частини відіграють роль вільних членів.

Для розв¢язання такої системи можна використати один із методів: формули Крамера, матричний спосіб, метод Гаусса, метод Жордана-Гаусса. Одержимо розв¢язок системи, де r невідомих будуть виражені через решту (n-r) невідомих, які мають назву незалежних невідомих.

Якщо надати цим невідомим довільні числові значення, то одержимо загальний розв¢язок системи. Щоб одержати часткові розв'язки системи, достатньо зафіксувати значення незалежних змінних.

Читайте також:

1. Active-HDL як сучасна система автоматизованого проектування ВІС.
2. B. Тип, структура, зміст уроку і методика його проведення.
3. D – моделювання в графічній системі КОМПАС
4. D) методу мозкового штурму.
5. D. СОЦИОИДЕОЛОГИЧЕСКАЯ СИСТЕМА ВЕЩЕЙ И ПОТРЕБЛЕНИЯ
6. Demo 11: Access Methods (методи доступу)
7. Demo 7: Модель OSI (модель взаімодії відкритих систем)
8. H) інноваційний менеджмент – це сукупність організаційно-економічних методів управління всіма стадіями інноваційного процесу.
9. I Метод Шеннона-Фано
10. I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
11. I. Метод єдиної подібності.
12. I. Метод рiвних вiдрiзкiв.

Переглядів: 1180