• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Розв’язання.

Множення та ділення додатних дійсних чисел.

Розв’язання.

Оскільки Ö3=1,7320508… і Ö2=1,4142135…, то знайдемо десяткові наближення цих чисел з точністю до сотих. Маємо 1,73≤Ö3≤1,74 і 1,41≤Ö2≤1,42. Тоді 1,73-1,42≤Ö3-Ö2≤1,74-1,41. Отже, 0,31≤Ö3-Ö2≤0,33. Випадки а) і б) пропонуємо студентам розглянути самостійно.

5. Розглянемо правила множення та ділення додатних дійсних чисел. Для цього пригадаємо, що нерівності одного смислу з додатними числами можна почленно множити. Розглянемо два дійсних числа αі β з їхніми відповідними наближеннями α_n′≤α_n≤α_n′′ і β_n′≤β_n≤β_n′′, де α≥0 і β≥0. Можна стверджувати справедливість наступної нерівності: α_n′•β_n′≤α_n•β_n≤α_n′′•β_n′′, яка дозволяє сформулювати наступне правило множення додатних дійсних чисел.

Правило: добуток двох додатних дійсних чисел α і β більший або дорівнює значення добутку десяткових наближень цих чисел, взятих з недостачею та менший або дорівнює значення добутку десяткових наближень цих чисел, взятих з надлишком.

Символічно маємо таку нерівність: α_n′•β_n′≤α_n•β_n≤α_n′′•β_n′′. Це правило можна поширити на будь-яку скінченну кількість співмножників. Проілюструємо застосування цього правила на наступних прикладах.

Вправа:знайти добуток дійсних чисел α=0,121121112… і β=1,242242224… з точністю до: а) цілих; б) десятих; в) сотих; г) тисячних.

Десятковим наближенням числа α до тисячних з недостачею буде 0,121, а з надлишком – 0,122. Для числа β будемо відповідно мати 1,242 і 1,243. Тепер можна за сформульованим правилом визначити значення суми чисел α і β з точністю до тисячних: 0,121•1,242≤α•β≤0,122•1,243. Отже, 0,150≤α•β≤0,152. Решту випадків пропонуємо студентам розглянути самостійно.

Виходячи із означення добутку дійсних чисел легко довести справедливість такої теореми.

Теорема: добуток дійсних чисел існує, єдиний, підкоряється комутативному та асоціативному законам і пов'язаний з дією додавання дистрибутивним законом.

Символічно цю теорему можна записати так: 1) ("α,βєR)($!γєR)(α•β=γ); 2) ("α,βєR)(α•β=β•α); 3) ("α,β,γєR)((α•β)•γ=α•(β•γ)); 4) ("α,β,γєR)(α•(β+γ)=α•β+α•γ).

Означення: часткою двох дійсних чисел α і β≠0 називають таке третє дійсне число γ, яке в добутку з числом β дає число α.

Символічно це означення можна записати так: (γ=α:β)↔(β•γ=α). Легко довести справедливість такої теореми та переконатися у справедливості наступного правила.

Теорема: частка двох дійсних чисел α і β≠0 завжди існує та єдина.

Правило:щоб знайти частку двох дійсних чисел α і β≠0 потрібно ділене помножити на число, обернене до дільника.

Символічно це виглядає так α:β=α•(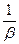). Наприклад: Ö5:Ö3=Ö5•(). Для практичного виконання ділення дійсних чисел, які виражені нескінченними неперіодичними десятковими дробами, використовують їхні десяткові наближення. Якщо маємо α_n′≤α_n≤α_n′′ і β_n′≤β_n≤β_n′′, де α≥0 і β≥0, то ≤≤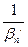. Тоді (α_n′:β_n′′)≤(α_n:β_n)≤(α_n′′:β_n′).

Правило: частка двох дійсних чисел α і β≠0 більша або дорівнює частки числа α з недостачею та числа β з надлишком і менша або дорівнює частки числа α з надлишком і числа β з недостачею.

Символічно це означення записується так: (α_n′:β_n′′)≤(α_n:β_n)≤(α_n′′:β_n). Застосування правила покажемо на наступному прикладі.

Вправа: знайти частку чисел Ö3 і Ö2 з точністю до: а) цілих; б) десятих; в) сотих.

Читайте також:

1. Міжнаціональні відносини і причини виникнення міжнаціональних конфліктів, шляхи їх розв’язання. Міжконфесійні стосунки та їх вплив на життя в полікультурному суспільстві
2. Поняття біосфери та ноосфери. Поняття екології. Основні завдання соціальної екології. Сучасні екологічні проблеми, причини їх виникнення та розв’язання.
3. Розв’язання.
4. Розв’язання.
5. Розв’язання.
6. Розв’язання.
7. Розв’язання.
8. Розв’язання.
9. Розв’язання.
10. Розв’язання.
11. Розв’язання.
12. Розв’язання.

Переглядів: 667