• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Диференціальні рівняння 1-го порядку.

У загальному випадку диференціальне рівняння першого порядку може бути записано у вигляді

.

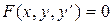Рівняння виду

(1)

або

, (2)

а також рівняння, котрі за допомогою алгебраїчних перетворень приводяться до рівнянь (1) або (2), називаються рівняннями з відокремлюваними змінними.

Відокремлювання змінних в рівняннях (1), (2) виконується за таким способом. Припустимо, що , 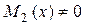і розділимо обидві частини рівняння (1) на . Для рівняння (2) обидві його частини помножимо на dx і розділимо на 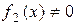. В результаті отримаємо рівняння з відокремленними змінними

, ,

котрі інтегруються за формулою

, .

.

Означення. Рівняння

, (4)

лінійне стосовно невідомої функції y та її похідної , називається лінійним диференціальним рівнянням першого порядку.

Такого типу рівняння може бути розв’язано методом варіації довільної сталої за таким способом. Замість сталої C в розв’язку однорідного рівняння введемо нову функцію 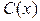, і в якості розв’язку неоднорідного ріняння (1) будемо розглядувати

, (5)

де будемо розшукувати невідому функцію .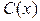

Диференціювання (5) дає

. (6)

Підставляючи (5) і (6) в дане рівняння, одержимо

,

тобто

® .

Інтегруванням останнього результату знаходимо

.

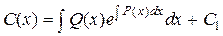Отже, загальний розв’язок рівняння (4) завжди може бути записаний у вигляді

, (7)

де C - довільна стала.

6.3. Диференціальні рівняння 2-го порядку.

Лінійне диференціальне рівняння другого порядку з сталими коефіцієнтами має вигляд:

у΄΄+р у΄+qy=0, (1)

де р і q – сталі дійсні числа.

Будемо шукати частинний розв’язок у вигляді y = e^kx, тоді

у΄= k e^kx , у΄΄= k² e^kx

к² e^kx+рк e^kx+ q e^kx=0

e^kx(к²+ pk+ q)=0

k²+pk+ q=0 (2)

Рівняння (2) називається характеристичним. Розв’язавши його, знайдемо два частинні розв’язки рівняння (1): .

Розглянемо 3 випадки:

1) Корні характеристичного рівняння дійсні, різні.

Тоді у₁ = e^k1x , у₂ = e^k2x і загальний розв’язок:

у=С₁ e^k1x + С₂ e^k2x, с_1, с₂ – довільні сталі.

2) Корені характеристичного рівняння дійсні і рівні, кратні. Якщо k є двократний корінь характеристичного рівняння, то йому відповідають два різних частинних розв’язки, а саме

у₁ = e^kx , у₂ = хe^kx.

Загальний розв’язок буде у= e^kx(С₁+ С₂х), с_1, с₂ – довільні сталі.

3) Корені характеристичного рівняння комплексні:

к₁=α+βі; к₂= α-βі, де .

Тоді частинні розв’язки: у₁ = e^(α+βі)х, у₂ = e^(α-βі)х.

Користуючись показниковою формою комплексного числа і його похідними, можемо записати

у₁ = e ^αхcosβх, у₂ = e ^αхsіnβх.

Загальний розв’язок: у=e ^αх(с₁ cosβх+ с₂sіnβх), с_1, с₂ – довільні сталі.

Читайте також:

1. V Процес інтеріоризації забезпечують механізми ідентифікації, відчуження та порівняння.
2. VІI. Утворіть вищий та найвищий ступені порівняння від прислівників із вправи VI.
3. Асимптотичний підхід до порівняння оцінок
4. Афінний шифр k-ro порядку.
5. Бінарне відношення порядку.
6. Бюджетний контроль - це порівняння показників бюджету зі звітом за від­повідний період часу.
7. В обох випадках основним розрахунковим рівнянням є рівняння теплопередачі і теплового балансу
8. Векторне канонічне параметричне рівняння прямої в просторі.
9. Вивід основного рівняння фільтрації
10. Визначення типу порівняння даних
11. Використання рівняння номінальних витрат за моделлю COCOMO II
12. Відбулися кардинальні зміни у світовому порядку. На авансцену виходить Європа1.

Переглядів: 837