• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тоді кореляційний момент можна записати у вигляді

K_ху = М_xy – М_x М_y. (3.28)

Згідно з властивостями математичного сподівання добутку двох незалежних випадкових величин (2.21) маємо М (х × у) = М_x × М_y.

Тоді кореляційний момент у формулі (3.28) для незалежних величин Х і Y буде

К_ху = М_x М_y – М_x М_y = 0.

Приклад 3.Між випадковими величинами Х і Y системи (х,у)є кореляційний зв’язок у вигляді у = ах + b.Довести, що при цьому коефіцієнт кореляції | r| = 1.

Розв’язання. Згідно з властивостями математичного сподівання (§ 3, розд.2) визначимо математичне сподівання функції у

М_y = М [ах + b] = аМ_x + b.

За формулою (3.21) обчислимо кореляційний момент

K_xy = M [(x – M_x) (y – M_y)] = M [(x – M_x) (ax +b – аМ_x – b)] =

= aМ [(x – M_x) (x – M_x)] = aM [(x – M_x )²] = aD_x = a .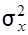

За формулою (3.24) коефіцієнт кореляції буде дорівнювати

.

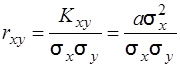Із рівняння у = ах + b визначимо стандарт функції у, виходячи з властивостей дисперсії (§ 3, розд.2) D_y = a² D_x і s_у = аs_х .

Тоді

.

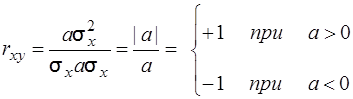§ 4. Багатовимірний розподіл. Числові характеристики системи довільного числа випадкових величин

Якщо система включає більше двох величин, то її розглядають як випадкові точки або випадкові вектори в просторі відповідної кількості п-вимірів.

Повною характеристикою системи п-випадкових величин (Х₁, Х₂, ..., Х_п) є закон розподілу цієї системи. Його задають функцією розподілу або щільністю розподілу.

Функцію п-аргументів х₁, х₂, ..., х_п, що дорівнює ймовірності спільного виконання п-нерівностей Х_і < x_i (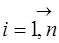) називають функцією розподілу системи (Х₁, Х₂, ..., Х_п),тобто

F (х₁, х₂, …, х_п) = P (Х₁ < x₁, Х₂ < x₂, …, Х_n < x_n). (3.29)

Граничне відношення ймовірності появи системи (Х₁, Х₂, ...,Х_п) в невеликих межах навколо точки (х₁, х₂, …, х_п)до розміру інтервалу межі при необмеженому його зменшенні називають щільністю розподілуj(х₁, х₂, ..., х_п) системи пвипадкових величин

j(х₁, х₂, ..., х_п)= 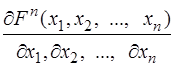.(3.30)

Якщо закон розподілу системи п-випадкових величин (Х₁, Х₂, ..., Х_п)невідомий, то її характеризують числовими характеристиками:

1. Математичним сподіванням М_x

М_x = 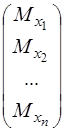, (3.31)

де 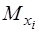– обчислюються за формулами (2.15 – 2.17).

2. Дисперсією D_x

D_x = . (3.32)

Дисперсії 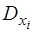характеризують міру точності кожної з випадкових величин, тобто розсіювання випадкової точки в напрямку осей і обчислюються за формулами (2.26 – 2.28).

3. Кореляційною матрицею K_x

Вона є узагальненим поняттям дисперсії D_x для випадкового вектора Х. Визначається за формулою

K_x = М [(X – M_x) (X – M_x)^T]. (3.33)

Відомо, що математичне сподівання випадкової матриці є матриця, складена із математичних сподівань її елементів. У формулі (3.33) приймемо п = 3, отримаємо

(x₁ - )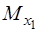

K_x = М (x₂ - 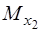) (x₁ - 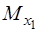) (x₂ - 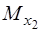) (x₃ - ) =

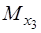(x₃ - )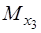

= …

… .

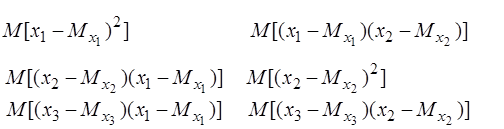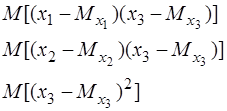
Згідно з формулами (2.26) і (3.21) маємо:

K_x = = ,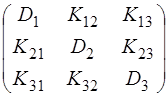

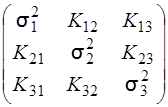де 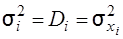– дисперсії Х_і, а K_ij = 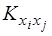– кореляційні моменти випадкових величин Х_ііХ_j.

При п-випадкових величинах системи (Х₁, Х₂, ..., Х_п) кореляційна матриця має вигляд

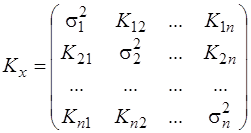. (3.34)

Аналіз формули (3.34) показує, що діагональні елементи кореляційної матриці 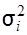є дисперсіями випадкових величин Х_і, а недіагональні елементи K_ij є кореляційними моментами між випадковими величинами Х_і і Х_j. Крім того, кореляційна матриця K_x симетрична відносно головної діагоналі, тобто

.

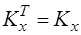Якщо випадкові величини системи (Х₁, Х₂, ..., Х_п)незалежні між собою, то матриця K_x буде діагональною

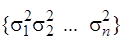= . (3.35)

Якщо всі дисперсії матриці (3.35) рівні між собою, 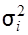= = 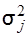то

K_x = s²E, (3.36)

де Е – одинична матриця.

Через кореляційні моменти K_ij можна обчислити коефіцієнти кореляції, що визначають міру зв’язку між парами Х_і і Х_j випадкових величин за формулою

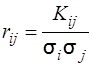. (3.37)

На заміну кореляційної матриці можна скласти нормовану кореляційну матрицю.

Нормованою кореляційною матрицею 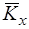називають матрицю, елементами якої є коефіцієнти кореляції r_ij, тобто

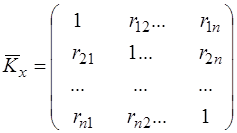. (3.38)

Якщо випадкові величини Х₁, Х₂, ..., Х_п мають нормальний розподіл і незалежні між собою, то система випадкових величин (Х₁, Х₂, ..., Х_п)буде п-вимірним нормальним розподілом зі щільністю ймовірності

j(х₁,х₂, ..., х_п) =

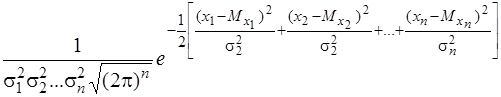= . (3.39)

Щільність нормального розподілу для системи двох залежних величин Х і Y буде

j(х,у) =

= .

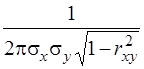
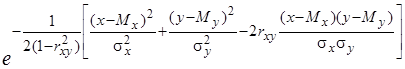(3.40)

Як видно із формули (3.40), для двох залежних випадкових величин закон розподілу визначається п’ятьма параметрами: М_x, М_y, s_х, s_у і r_xy.

Формула щільності нормального розподілу для системи (Х₁, Х₂, ..., Х_п)залежних випадкових величин Х₁, Х₂, ..., Х_пмає досить складний вигляд.

§ 5. Функції випадкових величин. Числові характеристики. Кореляційна матриця системи функцій випадкових

величин

В практиці геодезичних вимірювань виникають задачі оцінки точності результатів, що є функціями однієї чи декількох виміряних величин. Отримані функції теж будуть випадковими величинами. Як правило, відомо закон розподілу системи випадкових аргументів і відома функціональна залежність. Тобто, є система випадкових величин (Х₁, Х₂, ..., Х_п) і законїх розподілу. Розглянемо функцію Y від випадкових величин Х₁, Х₂, ..., Х_п

Y = f (Х₁, Х₂, ..., Х_п). (3.41)

Практично вирішують задачу визначення закону розподілу випадкової величини Y, виходячи з функції (3.39) і закону сумісного розподілу її аргументів Х₁, Х₂, ..., Х_п.

Покажемо вирішення цієї задачі для двох випадкових величин. Маємо функцію

Y = f (X₁, X₂).

Очевидно, що щільність розподілу системи випадкових величин (Х₁, Х₂) буде – j(x₁, x₂).

Штучно введемо нову величину Y₁ = X₁ і розглянемо систему двох рівнянь

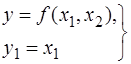.(3.42)

Очевидно, цю систему можна однозначно визначити відносно х₁та х₂, тоді

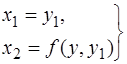.(3.43)

Виходячи з того, що система (3.43) диференціюється в теорії ймовірностей, доводиться, що щільність розподілу випадкової величини у = f(x₁, x₂) в нескінченних межах буде

j(у)= 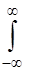j[x₁j y,x₁)] 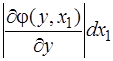. (3.44)

За аналогією находять щільність розподілу для функції трьох і більше випадкових величин. Наприклад, якщо Y = f(x₁, x₂, x₃), вводять нові перемінні

Y₁ = X₁,

Y₂ = X_2.

Якщо при цьому між системами (Х₁, Х₂, Х₃)і (Y, Y₁, Y₂)виявляється однозначне співвідношення, то щільність розподілу випадкової величини Y буде

j(у)= 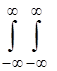j[x₁,х₂, j(y,x₁,х₂)] 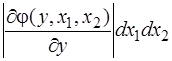, (3.45)

де j(y, x₁, x₂) – зворотня функція.

На основі формули (3.44) визначають щільність розподілу для випадкових величин: у = (x₁ + x₂); у = (x₁ - x₂); у = x₁ × x₂та 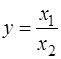[8;15].

Наприклад. Закон розподілу величини відхилення випадкової точки (Х,Y)від початку координат при умові, що система випадкових величин (Х,Y)має нормальний розподіл з параметрами М_х = М_y = 0іs_х = s_у=s називають розподілом Релея.

Зазначимо, що щільність розподілу такої системи (Х, Y)має вигляд

j(х,у) = .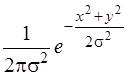

Відхилення точки (х,у)від початкукоординат буде визначатися випадковим вектором R, що є функцією випадкових величин Х та Y, тобто

.

Випадкова величини Rє полярним радіусом, тоді

x = r cos q;

y = r sin q.

Щільність розподілу j(r,q)системи випадкових величин (R, q)визначають через щільність розподілу j(х, у)системи (Х, Y).

Внаслідок математичних перетворень щільність розподілу випадкової величини Rвизначається розподілом Релея за формулою

j(r)= 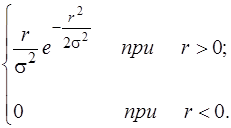.(3.46)

Графік розподілу Релея показано на рис. 3.4

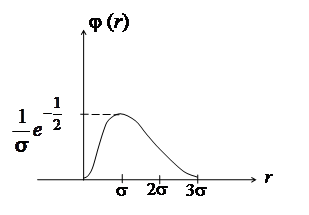Рис. 3.4

При дослідженнях не завжди виникає необхідність у визначенні закону розподілу функції випадкових величин. Тоді обчислюють числові характеристики функції випадкових величин: математичне сподівання та дисперсію.

Читайте також:

1. I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ
2. II. Організаційний момент.
3. Internet. - це мережа з комутацією пакетів, і її можна порівняти з організацією роботи звичайної пошти.
4. M – моменты
5. Адміністративні методи управління можна умовно поділити на організаційні та оперативно-розпорядчі.
6. Алгебраїчний момент пари сил
7. Аналітичний вираз сил і моментів.
8. Безрозмірною характеристикою гідротрансформатора називається залежність коефіцієнтів пропорційності моментів насосного і турбінного коліс від його передаточного відношення.
9. Біомаса - Кількість живої речовини на одиниці площі чи об'єму місцеперебування в момент спостереження. Визначається сумою біомаси усіх популяцій, що населяють дану екосистему.
10. В положение ее в данной момент времени (приращение радиуса-вектора точки за рассматриваемый промежуток времени), называется переменками.
11. В соответствии со ст.412.13 УПК РФ Постановление Президиума Верховного Суда Российской Федерации вступает в законную силу с момента его провозглашения.
12. Важливою ознакою класифікації є принцип побудови перетворювачів кодів, згідно з яким їх можна поділити на чотири групи.

Переглядів: 1092