• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Приклади розв’язання задач до розділу 3

Задача 1. У договорі двох комерційних фірм зазначено, що сторони вважають еквівалентними суми 10 тис. грн. сьогодні і 24414 грн. через чотири роки. Чи можна за цими даними визначити, який відсоток на валютний внесок забезпечуватимуть банки протягом чотирьох найближчих років?

Розв’язання

В даному випадку ставка банківського відсотка визначається як ставка дисконтування з формули: PV = FV/(1+i)ⁿ , тобто 10000=24414/(1+i)⁴. Звідси ставка дисконтування – ставка відсотка – складає 25% річних.

Задача 2. Кіт Матроскін вирішив купити корову за 2700 грн. Він очікує одержати такі прибутки: у першому році 480 грн., у другому – 750, у третьому–1250, у четвертому— 1000, у п'ятому — 500 грн. на шостий рік він її продасть за 1000 грн. на м'ясо. Ставка відсотка становить 20 % річних.

Чи доцільне його інвестиційне рішення? Якою буде сьогодні­шня цінність усього прибутку за 6 років?

Розв’язання

Для оцінки доцільності інвестицій використовують чисту сучасну цінність (NPV) або чистий дисконтова ний дохід (ЧДД), яку розраховують за формулою (3.15). Критерій NPV означає що інвестиції вигідні, якщо сьогоднішня цінність очікуваних грошових потоків перевищує інвестиційні витрати, тобто PV > K.

Сьогоднішня цінність майбутніх грошей у t-тому році визначається за формулою (3.12).

PV для першого року = = 400;

PV для другого року = = 521;

PV для третього року = = 723;

PV для четвертого року = 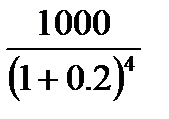= 482;

PV для п’ятого року = 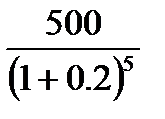= 201;

PV для шостого року = 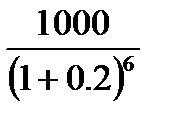= 335;

Сьогоднішня цінність майбутніх прибутків дорівнює:

400 + 521 + 723 + 482 + 201 + 335 = 2662 грн.

Оскільки інвестиційні витрати більші за сьогоднішню цінність майбутніх потоків грошей, то купувати Матроскіну корову недо­цільно.

Задача 3. Пан Везучий виграв у лотерею Кено джек-пот. Є два варіант виплати:

І – одержувати 470 тис. грн щороку до самої смерті;

ІІ – одержати 1 млн. грн через рік, 2 млн. грн — наприкінці дру­гого року і 3 млн. грн – наприкінці третього року. Ставка відсотка — 10%.

Якому з варіантів він надасть перевагу?

Розв’язання

Необхідно порівняти сьогоднішню цінність майбутніх потоків грошей PV (ДД) в обох випадках. У варіанті І приклад постійних виплат необмежений час. У цьому випадку сьогоднішня цінність майбу­тніх потоків грошей така:

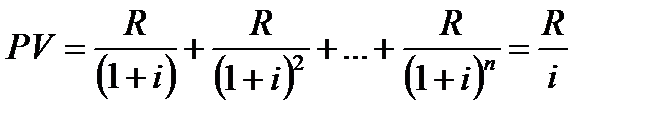
де R = 470 тис. грн.; i = 0,1;

тис. грн.=4,7 млн. грн.

Для другого варіанта:

млн. грн.

Отже, вигідніший другий варіант.

Задача 4. Пропозиція землі на околиці міста становить 100 га. Попит садоводів на землю: Q_c = 300–P, попит будівельних компаній на землю: Q_c = 700–2Р, де Р – ціна в тис. грн, ставка банківсь­кого відсотка – 10 %.

Визначте:

1. Ціну землі, якщо власник ділянки захоче її продати;

2. Хто зможе її купити і чому;

3. Щорічну орендну плату;

4. Земельну ренту, якщо щорічна амортизація дорівнює 5 тис. грн, а вкладений капітал – 20 тис. грн.

Розв’язання

1. Оскільки попит садоводів та попит будівельних компа­ній є взаємовиключними, то земельна ділянка буде продана тому, хто готовий заплатити більшу ціну. При абсолютно нееластичній пропозиції ціна садоводів дорівнює 200 тис. грн. (300-Р = 100), а ціна будівельних компаній 300тис. грн. (700-2Р= 100).

2. Зможуть купити цю ділянку будівельні компанії, оскільки вони готові заплатити вищу ціну.

3. Щорічна орендна плата: 300∙0,1 = 30 тис. грн.

4. До орендної плати, крім земельної ренти, включається що­річна амортизація та доход на вкладений капітал. Отже, земельна рента становить 30 – 5 – 20 *0,1 = 23 тис. грн.

Задача 5.Коту Матроскіну пропонують купити ділянку землі за 30 тис. грн., орендна плата за землю становить 5,4 тис. грн. щороку. Ставка банківського відсотка — 10 % річних.

Визначте:

1. Чи слід Матроскіну погоджуватися, якщо він має такі гроші в наявності;

2. Чи слід йому погоджуватися, якщо в нього є в наявності лише половина необхідної суми;

3. Яку мінімальну власну суму грошей йому слід мати, щоб погодитися на покупку, якщо він може розмістити свої гроші на депозит за меншою ставкою відсотка, ніж вказана вище.

Розв’язання

1. Оскільки ціна землі становить 54 тис. грн. (5,4/0,1 = 54), а пропонують купити за 30 тис. грн., то Матроскіну слід погодитися.

2. Якщо Матроскін візьме половину необхідної суми в кредит, то його щорічні виплати за кредитом становитимуть:

15 * 0,1 = 1,5 тис. грн.

Купівля ділянки землі за 30 тис. грн. рівнозначна орендній платі 3 тис. грн. за рік. Оскільки сума отриманої орендної плати за землю 5,4 > 4,5 де 4,5 = (1,5 + 3), то Матроскіну буде вигідно купувати землю.

3. Якщо виразити мінімальну суму власних грошей через X, то сума кредиту становитиме 30-X, знаходимо X з рівняння: (30 – X) * 0,1 + 30 * *0,1 = 5,4.

Звідси X= 6 тис. грн.

Читайте також:

1. I. Застосування похідної та інтеграла до роз’язування задач елементарної математики.
2. IV. Перевірка розв’язання і відповідь
3. А) Задачі, що розкривають зміст дій
4. АВТОМАТИЗАЦІЯ РОЗВ’ЯЗУВАННЯ КОМПЛЕКСУ ЗАДАЧ З ОБЛІКУ ОСНОВНИХ ЗАСОБІВ ТА НЕМАТЕРІАЛЬНИХ АКТИВІВ
5. Активи, що реалізуються повільно (А3) – це статті 2-го розділу активу балансу, які включають запаси та інші оборотні активи (рядки 100 до 140 включно, а також рядок 250).
6. Актуальні проблеми регіональної політики та їх розв’язання.
7. Алгоритм розв’язання
8. Алгоритм розв’язання
9. Алгоритм розв’язання задачі
10. Алгоритм розв’язання задачі
11. Алгоритм розв’язання розподільної задачі
12. Алгоритм розв’язування задачі

Переглядів: 3166