Висловлення. Прості і складені висловлення

Кожне математичне речення характеризується змістом і логічною структурою. В математиці виділяють елементарні (прості) речення та складені. Наприклад: «Число 12 ділиться на 3» - просте речення ; «Число 42 - парне і ділиться на 3» - складене. Складені речення утворюються з елементарних та з логічних зв’язок . Логічні зв’язки - це слова : «і», «або», «не», «якщо, то», «тоді і тільки тоді» та інші.

Визначити логічну структуру математичного речення означає встановити :

з яких елементарних речень складене дане речення;

за допомогою яких логічних зв’язок воно утворене.

Речення позначаються великими буквами латинського алфавіту: А, В, С і т.д.

Логічна структура речень може мати такий вигляд: «А і В», «не А», «якщо А, то В», «А або В», «А тоді і тільки тоді, коли В».

Наприклад: речення – «Число 36 ділиться на 4 і 9» має логічну структуру – «А і В», де А – «Число 36 ділиться на 4», В – «Число 36 ділиться на 9», логічна зв’язка «і».

Висловлення - це речення, відносно якого має смисл питання, істинне воно, чи хибне.

Висловлення – це обов’язково стверджувальне речення . Наприклад: «3 + 2 = 5»; «7 < 8»; «Н₂ S0₄ – кислота»; «Будь-який прямокутник є чотирикутником» і т.д. Висловлення, як і речення, позначаються великими літерами латинського алфавіту: А, В, С,....

Всі висловлення можна поділити на два класи: клас істинних і клас хибних висловлень. Отже, кожному висловленню можна поставити у відповідність одне з двох значень: І (істинне), або X (хибне), які називаються значеннями істинності.

Наприклад: висловлення «Число 125 ділиться на 5» – істинне, значення його істинності – І, а висловлення «5 < 3» - хибне, його значення істинності –X».

Висловлення поділяють на прості (елементарні) та складені. Значення істинності простих висловлень визначають за змістом, спираючись на відомі знання. Щоб встановити значення істинності складених висловлень, треба знати їх логічну структуру та смисл операцій над висловленнями.

3. Розглянемо операції, за допомогою яких із двох або більше простих висловлень можна будувати складені, та правила встановлення їх значень істинності.

Кон’юнкцією двох висловлень А і В називається складене висловлення (читається А і В), яке істинне тоді і тільки тоді, коли істинні обидва висловлення А і В, що його утворюють, і хибне в усіх інших випадках.

Кон’юнкцію двох висловлень дістають з двох простих, об’єднавши їх словом «і». Наприклад: «Середня лінія трикутника паралельна його основі і дорівнює її половині»; «24 - парне число і ділиться на 6».

Кон’юнкцію у математичній логіці називають логічним добутком. Значення істинності кон’юнкції висловлень можна подати за допомогою таблиці :

А	В
І	І	І
І	X	X
X	І	X
X	X	X

Наприклад, висловлення: «Число 15 - парне і ділиться на 3» має логічну структуру , де А - просте висловлення: «Число 15 – парне»; В – «Число 15 ділиться на 3». Значення істинності висловлення = X, бо А – Х, В – І.

Диз’юнкцією двох висловлень називається складене висловлення 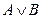(читається А або В), яке хибне тоді і тільки тоді, коли хибні обидва висловлення А і В, і істинне, якщо хоч би одне із них істинне.

Диз’юнкцію двох висловлень дістають, об’єднавши їх словом «або». Наприклад: «Рівняння х²-4=0 має корінь 2 або -2»; «Я поїду до Києва автобусом або поїздом».

Значення істинності операції диз’юнкції двох висловлень можна подати за допомогою таблиці:

А	в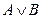
І	І	І
І	X	І
X	І	І
X	X	X

Наприклад: висловлення «5 > 2» має логічну структуру 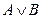, що є диз’юнкцією двох висловлень; А: «5 більше 2», В: «5 дорівнює 2»; значення істинності його – І, бо А – X, В – І, а тому за означенням диз’юнкці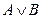ї –І.

Заперечення висловлення А є таке висловлення 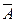, яке істинне тоді і тільки тоді, коли А - хибне, і хибне, якщо А - істинне.

Наприклад, дано висловлення: А – «Десна - притока Дніпра», тоді висловлення 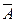– «Десна не є притокою Дніпра» або «Неправильно, що Десна є притокою Дніпра» - є запереченням даного висловлення.

Таблиця істинності для заперечення висловлення А має вигляд:

А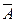
І	X
X	І

Наприклад:

А – «Число 3 є дільником числа 39» - істинне висловлення, тобто А = І, тоді його заперечення 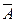– «Число 3 не є дільником числа 39» за означенням – хибне висловлення : 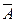– X.

Імплікацією висловлень А і В називається висловлення «якщо А, то В», позначається так: А=> В, яке хибне тоді і тільки тоді, коли А - істинне, а В - хибне.

Наприклад, висловлення: «Якщо два кути вертикальні, то вони рівні»; «Якщо 25 < 42. то 42 > 25» є імплікаціями. Вони мають логічну структуру «А => В». Знак " =>" - це знак відношення слідування.

У шкільному курсі математики доводиться дуже часто мати справу з імплікаціями. Так, наприклад, кожна теорема є імплікацією висловлень. В імплікації: «А=> В», висловлення А називається умовою або посилкою, а висловлення В - висновком або наслідком. Таким чином, імплікація буде хибним висловленням лише тоді, коли з правильної посилки дістанемо неправильний висновок.

Таблиця істинності для імплікації має такий вигляд :

А	В	А=> В
І	І	І
І	X	X
X	І	І
X	X	І

Запис А => В читають по-різному: «з А слідує В»; «В слідує з А»; «якщо А, то В», «є А, отже, є і В».Наприклад, висловлення «Якщо число а ділиться на 9, то воно ділиться на 3» можна прочитати і так: «3 того, що число а ділиться на 9, слідує, що воно ділиться і на 3» або «Число а ділиться на 3 слідує з того, що воно ділиться на 9», «Число а ділиться на 9, отже, воно ділиться і на 3».

Якщо з висловлення А слідує висловлення В, то кажуть, що В - необхідна умова для А, А- достатня умова для В.

А => В

В - необхідна умова для А

А - достатня умова для В

Якщо з висловлення А слідує висловлення В, а із висловлення В слідує висловлення А, то кажуть, що висловлення А і В рівносильні.

Висловлення «А рівносильне В» записують за допомогою знаку "<=>". Запис «А <=> В» читають так: «А рівносильне В», «А тоді і тільки тоді, коли В». Якщо висловлення А і В рівносильні, то кажуть, що А необхідна і достатня умова для В і навпаки. Таку операцію називають еквіваленцією.

Еквіваленцієюдвох висловлень А і В називається таке висловлення А<=>В, яке істинне тоді і тільки тоді, коли обидва висловлення А і В мають однакові значення істинності.

А	В
І	І	І
І	Х	Х
Х	І	Х
Х	Х	І

Наприклад: висловлення – «Число х ділиться на 3 тоді і тільки тоді, коли сума цифр цього числа ділиться на 3» - є еквіваленцією. Воно має логічну структуру А <=> В, де А - це висловлення : «Число х ділиться на 3», а В - це висловлення: «Сума цифр числа х ділиться на 3». Істинність цього твердження доводиться.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
ПЕРЕДМОВА	\|	Предикати (висловлювальні форми)

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.