• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Непрямі доведення.

Зведення до абсурду. Цей метод полягає в тому, що в теоремі А 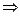В припускають, що правильним буде . Якщо в результаті цього припущення приходять до неправильного висновку, абсурду, то роблять висновок, що наслідок В теореми А 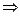В правильний.

Цим способом доводять, наприклад, таку теорему: Якщо дві різні прямі а і b паралельні третій прямій с, то вони паралельні між собою.

Припустимо , тобто а і b не паралельні. Тоді вони перетинаються в якійсь точці К, яка не належить с. Дістанемо, що через точку К поза прямою с можна провести дві прямі а і b, які паралельні с, а це суперечить аксіомі паралельності, тобто є хибним твердженням. Отже, правильним твердженням є В.

Метод від супротивного. Цей спосіб ґрунтується на законі контрапозиції А 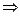В = .

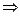
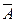Теорема: Довести, що коли аb– непарне число, то обидва множники а і b – непарні цілі числа.

Позначимо А: «добуток аb– непарне число», Т: «а – непарне число», S: «b – непарне число». Тоді теорема скорочено запишеться так:

A 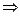S T, або А 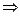В, де В «S T».

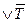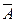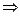
Припустимо, що = = , тобто один із множників а або b є парним числом. Нехай, наприклад, а – парне, тобто а = 2m, m Z. Тоді ab = 2mb – парне число, тоді дістали . Таким чином довели теорему 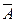, а цим самим і дану теорему А 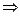В.

Поширеним прикладом неправильних міркувань є непродумане використання неповної індукції, коли загальний висновок зроблено на основі окремих спостережень, експериментів, розгляду скінченної кількості їх. Використання неповної індукції може привести як до правильних, так і неправильних висновків. Так, побудувавши кілька графіків лінійних рівнянь з двома змінними в прямокутній системі координат і побачивши, що вони є прямими лініями, робимо висновок, що графік кожного лінійного рівняння з двома змінними є пряма лінія. Цей умовивід – правильний. Прикладом, коли неповна індукція приводить до хибного результату є теорема Ферма. Ще у XVII ст. математик П. Ферма (1601 – 1665) помітив, що числа виду F_n =2²ⁿ+1 при n = 0, 1, 2, 3, 4 – прості: F₀ = 3, F₁ = 5, F₂ = 17, F₃ = 257, F₄ = 65537.

Ферма висловив припущення, що при будь-якому n N числа такого виду є простими (їх стали називати простими числами Ферма). Ця гіпотеза була висловлена на основі кількох обчислювальних експериментів. У 1732 р. видатний математик Л. Ейлер (1707 – 1783) показав, що при n = 5

F₅ = 4294967297 = 641 ∙ 6700417, тобто F₅ не є простим числом. Цей контрприклад спростував гіпотезу Ферма.

§ 3. Математичні поняття. Особливості математичних понять. Об'єм і зміст поняття. Означення понять. Структура означення понять через рід і видову відмінність

План

1. Поняття як форма мислення. Особливості математичних понять.

2. Зміст і обсяг поняття, відношення між ними.

3. Способи означення математичних понять.

4. Вимоги до означення понять.

5. Приклади математичних понять, які розглядаються в початковому курсі математики.

Читайте також:

1. Беззондові (непрямі) тести.
2. Доведення.
3. Доведення.
4. Доведення.
5. Доведення.
6. Доведення.
7. Доведення.
8. Доведення.
9. Доведення.
10. Доведення.
11. Доведення.
12. Доведення.

Переглядів: 555