• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Способи знаходження найбільшого спільного дільника і найменшого спільного кратного

І спосіб обчислення НСК і НСД за канонічним розкладом чисел

Знайдемо НСК і НСД чисел 360 і 525. Ці числа можна подати у канонічному вигляді: 360 = 2³ ∙ 3² ∙ 5; 525 = 3 ∙ 5² ∙ 7. У розклад на прості множники НСД цих чисел повинні ввійти всі спільні прості множники, причому кожний з них треба взяти з найменшим показником, з яким він входить в канонічні розклади даних чисел. Отже НСД(360, 525) = 3 ∙ 5 = 15.

У розлад на прості множники НСК (360, 525) повинні ввійти всі прості множники, які входять принаймні в один розклад, причому кожний з них треба взяти з найбільшим показником. НСК(360, 525) = 2³ ∙ 3² ∙ 5² ∙ 7 = 12 600.

Теорема:НСК (а, b) ∙ НСД (а, b) = а ∙ b.

Наслідок:Якщо НСК (а, b) = 1, то НСК (а, b) = а ∙ b .

ІІ спосіб обчислення НСК і НСД за алгоритмом Евкліда

Лема 1:Якщо а ділиться на b, то НСД (а, b) = b.

Лема 2:Якщо а = bq+ r, де а, b, r – натуральні числа, то НСД (а, b) = НСД (b, r).

Розглянемо алгоритм Евкліда для знаходження НСД довільних натуральних чисел а і b. Нехай а ≥ b. Якщо а 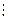b,то за лемою 1 НСД ((а, b) = b. Якщо а = bq+ r, де r ≠ 0, то за лемою 2 задача знаходження НСД зводиться до обчислення НСД чисел b, r, де r < b. Якщо b 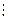r, то НСД (b, r)=r, а отже, і НСД(а, b) = r. Якщо при діленні b на r матимемо остачу 0 < r₁ < r, то b = rq₁+r₁, і тому НСД (а, b) = НСД (b,r) = НСД (r,r₁). Продовжуючи описаний процес, діставатимемо все менші і менші остачі: r, r₁, …, r_m. Зрештою дістанемо остачу, яка ділить попередню остачу. Згідно з лемою 2, ця, відмінна від нуля, остача і є НСД (а, b). Таким чином НСД двох натуральних чисел дорівнює останній, відмінній від нуля остачі в алгоритмі Евкліда для цих чисел.

Алгоритм Евкліда як спосіб послідовного ділення зручно записувати у вигляді многократного ділення кутом.

Знайдемо НСД(90, 35).

_ 90 35 Таким чином,

70 2 90 = 35 ∙ 2 = 20

_35 20

20 1 35 = 20 ∙ 1 + 15

_ 20 15

15 1 20 = 15 ∙ 1 + 5

_ 15 5

15 3 15 = 5 ∙ 3 + 0

Отже, остання відмінна від нуля остача дорівнює 5, тому НСД(90, 35) = 5.

Після обчислення за допомогою алгоритму Евкліда НСД двох чисел можна знайти НСК, використовуючи залежність між НСД і НСК. Так, НСК (90, 35) = 90 ∙ 35 : 5 = 630.

Читайте також:

1. II.3. Основні способи і прийоми досягнення адекватності
2. Алгоритм знаходження ДДНФ (ДКНФ) для даної булевої функції
3. Алгоритм знаходження найбільшого та найменшого
4. Алгоритм знаходження оптимального плану
5. Алгоритм знаходження початкового опорного плану
6. Алгоритм однократного заміщення Жордана-Гауса
7. Аналіз факторів впливу на обсяги виробництва суспільного продукту.
8. Багатофакторна матриця «Мак-Кінсі», її зміст, способи використання , достоїнства і недоліки.
9. Безстатеве розмноження, його визначення та загальна характеристика. Спори — клітини безстатевого розмноження, способи утворення і типи спор.
10. Біологічні способи лікування ран.
11. БУДОВА, ВЛАСТИВОСТІ МЕТАЛІВ ТА СПОСОБИ ЇХ ВИЗНАЧЕННЯ
12. В розвитку суспільного виробництва

Переглядів: 2174