
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Система допусків кутових розмірів та їх відхилень
Стандартна система допусків і характерів гладких конічних з'єднань побудована на базі системи ISO. Кутові розміри широко використовують для конічних поверхонь деталей пневмо- та гідроарматури, інструментальних конусів для хвостовиків різальних і вимірювальних інструментів; отворів у шпинделях обробних верстатів і допоміжних технологічних інструментів; фіксаторів, виливків, кованок тощо.
Класифікують кутові розміри так само, як і лінійні. Розрізняють розміри номінальні, граничні та істинні. Стандартом (ГОСТ 8908-81) встановлені ряди номінальних кутових розмірів з використанням рядів переважних чисел з деякими заокругленнями. Наприклад, перший ряд номінальних значень кутових розмірів має такий вигляд: 0; 5; 10; 15; 20; 30; 45; 75; 90; 120°;...; другий ряд: 0"; 30'; 1°; 2; 3; ...; 10; 40; 75°; ... тощо.

 На відміну від лінійних, які за основну одиницю мають метр і похідні від нього часткові та кратні одиниці, для вимірювання кутових розмірів встановлено дві одиниці: радіан (для плоского кута) та стерадіан (для просторового кута). Окрім цього, дозволено використовувати стару одиницю кутових розмірів — градус (°) та часткові одиниці (мінуту' та секунду "), що становлять відповідно одну шістдесяту частину старої одиниці.
На відміну від лінійних, які за основну одиницю мають метр і похідні від нього часткові та кратні одиниці, для вимірювання кутових розмірів встановлено дві одиниці: радіан (для плоского кута) та стерадіан (для просторового кута). Окрім цього, дозволено використовувати стару одиницю кутових розмірів — градус (°) та часткові одиниці (мінуту' та секунду "), що становлять відповідно одну шістдесяту частину старої одиниці.
Граничні кутові розміри отримують, підсумовуючи їх номінальні значення та граничні (верхнє чи нижнє) відхилення. Допуском кутового розміру АТα називають різницю між найбільшим і найменшим допускними кутовими розмірами, тобто
АТа = αmах - αmin .
У системі допусків кутових розмірів значення допусків обчислюють залежно від ступенів точності та довжини коротшої його сторони, незалежно від значення кута. Ступені точності позначені цифрами в порядку зменшення точності 1; 2; 3; ....; 16 і 17. Стандарт (ГОСТ 8908-81) допускає використання додаткових ( з меншими допусками) ступенів точності 0 і 01, значення допусків для яких отримують діленням значень допусків 1 ступеня послідовно на спільний дільник φ = 1,6.
 Розглянемо креслення вала крана з трьома конічними поверхнями: робочою поверхнею крана, виконаною у вигляді конуса Морзе №3 з точністю кутового розміру АТD6,яка згідно зі стандартом становить 0,012 мкм на заданій довжині 79мм твірної конуса, з шорсткістю поверхні 0,032 за параметром Rа, що притерта разом з конічною поверхнею корпуса; плоскою поверхнею внутрішнього отвору вала з кутом 7°±1°, отриманою під час лиття заготованки вала, та фаскою 1,5 x 45°, для якої точність кута не зазначена, що дає змогу виготовляти її за останнім, тобто 17 ступенем точності, з відхиленням даного розміру ±2°18' (рис. 3.10). За чинними стандартами є кілька способів позначати кутові розміри на кресленнях: цифровими значеннями номінальних розмірів та їх граничними відхиленнями (30°±2°; 10°±30'; 3°±15"; 25°^2; 25°-1; тощо); номінальними цифровими кутовими розмірами та літерними позначеннями їх точності; номерами ступенів точності (30°+АТа7; 30°-АТа9; 10°±0,5 АТа5); умовними позначеннями конусних поверхонь (метричний конус № 80 АТ6, конус Морзе № 4 АТ7), номінальними кутовими розмірами без написання допускних відхилень (фаска 1,5 х 45°; нахил 7°; нахил 1:10; конусність 1:5 тощо).
Розглянемо креслення вала крана з трьома конічними поверхнями: робочою поверхнею крана, виконаною у вигляді конуса Морзе №3 з точністю кутового розміру АТD6,яка згідно зі стандартом становить 0,012 мкм на заданій довжині 79мм твірної конуса, з шорсткістю поверхні 0,032 за параметром Rа, що притерта разом з конічною поверхнею корпуса; плоскою поверхнею внутрішнього отвору вала з кутом 7°±1°, отриманою під час лиття заготованки вала, та фаскою 1,5 x 45°, для якої точність кута не зазначена, що дає змогу виготовляти її за останнім, тобто 17 ступенем точності, з відхиленням даного розміру ±2°18' (рис. 3.10). За чинними стандартами є кілька способів позначати кутові розміри на кресленнях: цифровими значеннями номінальних розмірів та їх граничними відхиленнями (30°±2°; 10°±30'; 3°±15"; 25°^2; 25°-1; тощо); номінальними цифровими кутовими розмірами та літерними позначеннями їх точності; номерами ступенів точності (30°+АТа7; 30°-АТа9; 10°±0,5 АТа5); умовними позначеннями конусних поверхонь (метричний конус № 80 АТ6, конус Морзе № 4 АТ7), номінальними кутовими розмірами без написання допускних відхилень (фаска 1,5 х 45°; нахил 7°; нахил 1:10; конусність 1:5 тощо).
Окрім допусків кутових розмірів в кутових одиницях (радіан, градус), стандарт регламентує ще два додаткових способи написання значень відхилень за допомогою
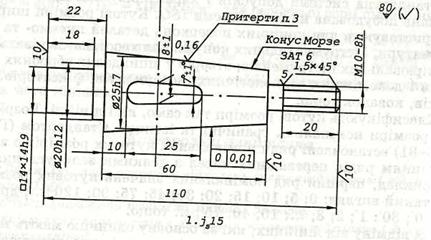
Рис. 3.10. Креслення вала з трьома конічними поверхнями
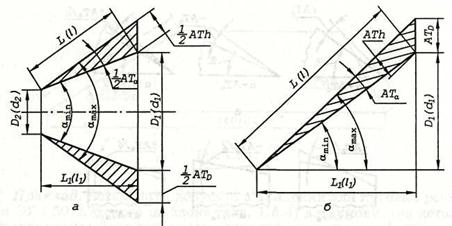
лінійних розмірів (рис. 3.11, а і б). Відхилення кута α, заданого в кутових одиницях, визначають також за допомогою допуску АТ діаметра D1 (d1) великої основи конуса, що містяться у площині, віддаленій на задану відстань L(l) від вершини кута чи базової поверхні конуса, або відрізка, перпендикулярного до твірної конуса АТh.. Обидва відхилення задають за допомогою лінійних розмірів.
Допуск АТ призначають для конічних поверхонь з конусністю, більшою від 1:3, залежно від довжини твірної конуса L(l). Залежність між допусками АТh і АТа як для конуса, так і для кутника можна записати у вигляді
 ,
,
де АТh— допуск кутового розміру, виражений довжиною відрізка, перпендикулярного до твірної конуса чи сторони кута кутника, мкм;
АТα — допуск кутового розміру, мкрад;
L — довжина твірної конуса чи сторони кутника, мм.
Значення допусків у кресленнях рекомендують, якщо це можливо, заокруглювати. Заокруглені значення допусків АТа наведені у стандарті (у кутових градусах, мінутах і секундах). Стандартні розміри довжини коротшої сторони кутів можуть мати розміри від 0 до 2500 мм. Цей діапазон поділено на менші діапазони, для кожного з яких наведено середні значення допусків для чотирьох способів їх визначення (АТа— у радіанах і градусах, АТD та АТh — у міліметрах). Як бачимо, залежність допусків від ступеня точності і від довжини коротшої сторони кута є значною. Наприклад, допуск для довжин коротшої сторони кута від 3 до 10 мм становить 10"— для 1 ступеня і 4°35'1" — для 17 ступеня точності.
|
Рис. 3.11. Написання відхилень за допомогою лінійних розмірів 

Стандарт регламентує три способи написання відхилень кутових розмірів: два однобічні та симетричний. Схема полів допусків для кутових розмірів зображена на рис. 3.12.
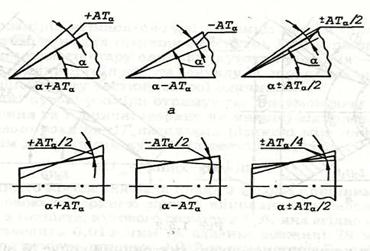
|
б
Рис. 3.12. Схема полів допусків для кутових розмірів
Читайте також:
- Active-HDL як сучасна система автоматизованого проектування ВІС.
- D. СОЦИОИДЕОЛОГИЧЕСКАЯ СИСТЕМА ВЕЩЕЙ И ПОТРЕБЛЕНИЯ
- II. Бреттон-Вудська система (створена в 1944 р.)
- III. центральная нервная система
- ISO9000. Як працює система управління якістю
- IV. Система зв’язків всередині центральної нервової системи
- IV. УЗАГАЛЬНЕННЯ І СИСТЕМАТИЗАЦІЯ ВИВЧЕНОГО
- The educational system of Great Britain (Система освіти Великобританії)
- V. СИСТЕМА ПОТОЧНОГО ТА ПІДСУМКОВОГО КОНТРОЛЮ ЗНАНЬ СТУДЕНТІВ
- V. Систематизація і узагальнення нових знань, умінь і навичок
- V. Узагальнення та систематизація знань учнів.
- V. Узагальнення та систематизація знань учнів.
| <== попередня сторінка | | | наступна сторінка ==> |
| | | Основні параметри конічного з’єднання |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |