• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Звичайні та особливі точки

Точка кривої лінії, яка за своїми властивостями не відрізняється від більшості інших точок кривої, є звичайною.

Звичайна точка має такі ознаки:

1) окіл звичайної точки є єдиною неперервною лінією;

2) у звичайній точці крива має тільки одну дотичну;

3) точка, що рухається вздовж кривої, до і після звичайної точки має єдиний напрям руху, а дотична в цій точці має певний напрям обертання навколо неї.

Крім звичайних, розрізняють особливі точки, в яких кривина має найбільше (найменше) значення, або порушуються властивості дотичної до кривої. Наприклад, найбільшу кривину еліпс має на кінцях A, B великої осі, а найменшу – на кінцях C, D малої осі, рис.3а; кривина дорівнює нулю в так званій точці перегину М, рис.3б.

Рис. 3.

До особливих точок належать також:

- точка перегину, в якій дотична змінює напрям обертання, рис. 4а;

- точка звороту першого роду (вістря), в якій напрям руху точки вздовж кривої змінюється на протилежний, а напрям обертання дотичної не змінюються, рис. 4б;

- точка звороту другого роду (дзьоб), де напрям руху точки вздовж кривої і напрям обертання дотичної змінюються на протилежний, рис. 4в;

- точка самодотику (повторення), де крива кілька разів дотикається до однієї прямої, рис. 4г;

- вузлова (подвійна) точка, в якій крива сама себе перетинає і має дві або більше дотичних, рис. 4д;

- точка злому, де порушується плавність кривої, рис. 4е.

Рис. 4.

2.4. Еволюта та евольвента

Множина нормалей до плоскої кривої a в точках N_i утворює в’язку, обвідною якої є крива b, яку називають еволютою, рис.5. Крива a відносно своєї еволюти b називається евольвентою. На еволюті b плоскої кривої a розміщена множина центрів кривини M_i кривої a. Дотичні до

Рис. 5.

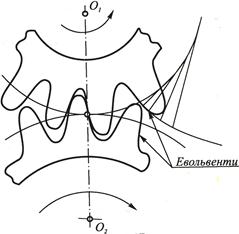еволюти b є нормалями у відповідних точках N_i евольвенти a. Одній еволюті b відповідає множина евольвент a. Ці криві, особливо евольвенти кола, мають широке використання у технічних формах, зокрема профілі зубців зубчатих передач мають форму евольвенти кола, рис.6.

Читайте також:

1. Алгебраїчний спосіб визначення точки беззбитковості
2. Аналіз точки беззбитковості
3. Антропометричні точки
4. Біологічна особливість репродукції людини
5. В положение ее в данной момент времени (приращение радиуса-вектора точки за рассматриваемый промежуток времени), называется переменками.
6. Валентність з точки зору будови атома.
7. Вибір прицілу, точки прицілювання та цілика
8. Видалення характерної точки
9. Визначення прямокутних зональних координат X та Y точки N на карті
10. Визначення точки
11. Визначення точки беззбитковості
12. Визначення точки беззбитковості

Переглядів: 1612