• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Розв’язання задачі з урахуванням власної ваги

Згідно з рис. 1.3,а та рис. 1.4,а,б,в визначаємо 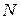і 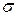на кожній з трьох ділянок.

Ділянка І ( ):

, , ,

.

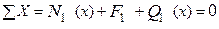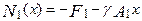При x = 0: ,

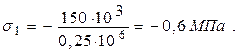
При x = 4 м:

(другий член у виразі для N₁ – це власна вага ділянки І Q₁=18 кH),

М_В 1:200 (указати обраний Вами вертикальний масштаб)

На епюрі N 1 см ~ 120 кН, а на епюрі s 1 см ~ 0,25 МПа (указати обрані Вами співвідношення)

Рис. 1.3

а) ділянка І б) ділянка ІІ в) ділянка ІІІ

Рис. 1.4

Ділянка ІІ ( ):

, ,

, .

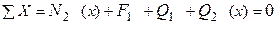При x = 4 м: ,

При x = 6 м:

(третій член у виразі для N₂ – це власна вага ділянки ІІ Q₂=18 кH),

Ділянка ІІІ ( ):

, ,

, .

При х = 6 м; ,

При x=11 м:

(п’ятий член у виразі для N₃ – це власна вага ділянки ІІІ Q₃=45 кH),

За отриманими даними будуємо епюри 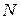і 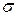(рис. 1.3,б,в).

Небезпечним буде нижній поперечний переріз бруса, де виникає . Умова міцності для цього перерізу виконується:

.

Таким чином міцність усього бруса з урахуванням власної ваги теж забезпечена. (Без урахування власної ваги .)

Повна деформація бруса дорівнює алгебраїчній сумі абсолютних деформацій усіх ділянок:

,

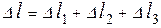де – абсолютні деформації ділянок бруса.

Визначаємо абсолютні деформації ділянок:

Тоді повна деформація бруса з урахуванням власної ваги буде такою:

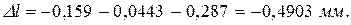
Без урахування власної ваги .

Переміщення перерізу I-I відносно жорсткого закріплення ( ) дорівнює алгебраїчній сумі абсолютних деформацій усіх частин бруса, розташованих між перерізом і закріпленням. У нашому випадку між перерізом і закріпленням розташована тільки частина третьої ділянки довжини 4 м і переміщення перерізу таке

,

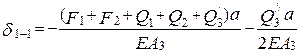де - власна вага верхньої частини ділянки І, а - власна вага нижньої частини цієї ж ділянки. Частини відсікаються перерізом I-I.

Підставимо числові значення величин

Без урахування власної ваги

Визначимо розміри квадратного поперечного перерізу кожної ділянки бруса, які забезпечать найменші витрати матеріалу.

З епюри 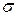видно, що небезпечні перерізи за нормальними напруженнями розташовані в кінці кожної ділянки. Для цих перерізів запишемо відповідні умови міцності, потім визначимо потрібні площі поперечних перерізів і відповідні їх розміри .

Для ділянки І: , звідки

.

Для ділянки ІІ: ,

де - нова вага ділянки І,

Для ділянки Ш: ,

де - нова вага ділянки ІІ,

Без урахування власної ваги , , .

Порівнявши відповідні величини, бачимо, що в розглянутому випадку урахування власної ваги необхідне.

Приклад розв’язання задачі № 2. Горизонтальний абсолютно жорсткий брус АВ підтримується стальними стержнями 1 і 2 (рис.1.5,а), кінці яких шарнірно закріплені. При а =1 м, b =4 м, с =2 м, d =3 м, A₁=4 см²=4·10^{-4 м2}, А₂ =6 см²=6·10^{-4 м2}, Е =2·10⁵ МПа, α=45^о і [σ]=160 МПа, потрібно визначити наступне: а) зусилля та напруження в стержнях (в частинах сили ); б) допустиме навантаження .

Скористаємось методом перерізів: розріжемо перший та другий стержні та залишимо верхню частину системи (рис. 1.5,б), зобразивши додатними невідомі поздовжні зусилля , (спрямувавши їх в бік відкинутої частини). Враховуємо, що в шарнірно-нерухомій опорі С присутні дві складові опорної реакції: і . Для визначення чотирьох невідомих ( , , і ) можна скласти лише три незалежні рівняння статики. Таким чином ССН=4-3=1 і система є один раз статично невизначеною. Для однозначного розв’язання задачі треба скласти одне додаткове рівняння – рівняння сумісності деформацій.

В задачі необхідно визначити тільки поздовжні зусилля і , тому з можливих трьох рівнянь статики залишаємо тільки одне: (до цього рівняння не увійдуть невідомі складові опорної реакції і ):

. (І)

а) б)

в)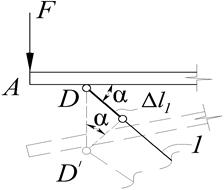

Рис. 1.5

Щоб скласти додаткове рівняння, розглянемо деформацію заданої системи. Побудуємо план переміщень (рис. 1.5,а): під дією зосередженої сили абсолютно жорсткий брус, не викривляючись, повернеться навколо опорного шарніру С і точка А зміститься вниз; перший стержень укоротиться (стиснеться) на величину поздовжньої деформації 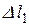, яку ми й відкладаємо вздовж початкового положення першого стержня (рис. 1.5,а,в); потім проводимо два перпендикуляри: один до жорсткого бруса через шарнір D, а другий до укороченого першого стержня (переміщення за дугами окружностей апроксимуємо переміщеннями за перпендикулярами, це можна робити з-за молості деформацій); там де вказані перпендикуляри перетинаються й буде нове положення вузла D'; орієнтуючись на вузли С і D', зображуємо нове положення бруса та першого стержня (штрихові лінії); вузол В, як належав нижній грані бруса до деформації системи, так і повинен їй належати й після деформації (вузол В'), тобто другий стержень подовжується на величину .

З подібності трикутників та маємо

. (ІІ)

Зважаючи на те, що і (рис. 1.5,а,в),

вираз (II) набуває такий вигляд:

. (ІІІ)

Це й є додаткове рівняння – рівняння сумісності деформацій стержнів 1 і 2.

У рівняннях статики, які складаються в методі перерізів, усі невідомі зусилля вважаються додатними й такими ж вони зображуються (розтягуючими на рис. 1.5,б). Проте, на деформованій схемі деякі стержні можуть бути стиснутими (стержень 1 на рис. 1.5,а). У цьому випадку, для приведення у відповідність знаків зусиль та деформацій, вирази для деформацій стиснутих стержнів треба записати зі знаком “–“.

Для даної задачі ,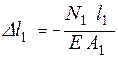

і рівняння сумісності деформацій (ІІІ) остаточно запишеться так:

. (ІV)

Визначимо довжини стержнів

, = d =3 м.

Підставивши в рівняння (I, IV) числові значення a, b, c, , , , та , отримуємо наступну систему рівнянь

,

.

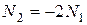Після розв’язання системи маємо

, .

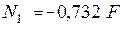Визначаємо нормальні напруження в стержнях

Як бачимо, найбільш напруженим (небезпечним) буде стержень 2 (в ньому виникає найбільше за абсолютним значенням нормальне напруження). Запишемо для нього умову міцності за нормальними напруженнями

,

з якої одержуємо допустиму величину зосередженої сили

Контрольні запитання

1. Назвіть види зовнішніх сил та відмітьте в яких одиницях вони вимірюються?

2. Що називають брусом та стержнем, пластиною, оболонкою, масивним тілом?

3. Що називається віссю бруса, стержня та що треба розуміти під поперечним перерізом?

4. Яким основним вимогам повинні задовольняти люба конструкція та її елементи? Які види розрахунків дозволяє виконати кожна зі згаданих умов?

5. Для чого введені в опір матеріалів гіпотези та розрахункові принципи?

6. Які основні гіпотези та розрахункові принципи використовуються в опорі матеріалів?

7. Що називають напруженням (механічним напруженням) та в яких одиницях вони вимірюються?

8. Що таке деформація тіла?

9. Що таке пружність та пластичність, пружна та пластична деформації?

10. Які зусилля (внутрішні силові фактори) виникають в довільному поперечному перерізі у загальному випадку та за допомогою якого методу вони визначаються? В чому полягає суть згаданого методу?

11. В яких одиницях вимірюються зусилля?

12. Які види простих деформацій ви знаєте?

13. Коли реалізується осьовий розтяг або стиск?

14. Як визначають поздовжні сили (зусилля) при осьовому розтягненні або стисненні?

15. Як визначають нормальні напруження, що виникають в поперечному перерізі при осьовому розтягненні або стисненні, та за яким законом вони розподілені по цьому перерізу?

16. Що називають епюрами та у якому порядку треба їх будувати?

17. Як записується умова міцності при осьовому розтягненні або стисненні та які типи задач розв’язуються з її допомогою?

18. Що таке допустиме напруження та як воно визначається для пластичних і крихких матеріалів?

19. Які основні причини змусили ввести коефіцієнт запасу міцності та які значення він може приймати?

20. Що називається границею пропорційності, пружності, текучості та міцності пластичного матеріалу?

21. Що називається границею міцності крихкого матеріалу?

22. Чим відрізняються діаграми розтягання та стискання у пластичних і крихких матеріалів?

23. Які матеріали відносять до пластичних, а які до крихких?

24. Які деформації називають абсолютними, а які відносними?

25. Як записується та формулюється закон Гука при осьовому розтяганні або стисканні?

26. Що характеризує модуль пружності?

27. Що відображує коефіцієнт Пуассона та у яких межах він змінюється для ізотропних матеріалів?

28. Як визначаються деформації бруса (стержня) при осьовому розтяганні або стисканні з урахуванням і без урахування власної ваги?

29. Коли необхідно враховувати власну вагу бруса (стержня)?

30. Як записується умова міцності з урахуванням власної ваги?

31. Що називають ділянками та що є межею ділянки?

32. У якій послідовності треба розраховувати східчастий брус?

33. Які системи називаються статично визначеними, а які невизначеними?

34. Які етапи треба виконати при розрахунку статично невизначених систем?

Читайте також:

1. IV. Перевірка розв’язання і відповідь
2. S Визначення оптимального темпу роботи з урахуванням динаміки наростання втоми.
3. А) Задачі, що розкривають зміст дій
4. А. Створення власної папки.
5. Абсолютна деформація ділянки бруса тільки від власної ваги визначається за формулою
6. Актуальні проблеми регіональної політики та їх розв’язання.
7. Алгоритм розв’язання
8. Алгоритм розв’язання
9. Алгоритм розв’язання задачі
10. Алгоритм розв’язання задачі
11. Алгоритм розв’язання розподільної задачі
12. Алгоритм розв’язування задачі

Переглядів: 2012