• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Метод половинного ділення (метод бісекцій)

Умова застосовності методу половинного ділення припускає безперервність функції ƒ(х) на проміжку [a ; b].

Уточнення значення кореня проводиться шляхом побудови послідовності, що сходиться

x_к =(а_к + b_к) / 2 , к = 1, 2, (1.4)

За а₁ , b₁ приймаємо відповідно а , b .

Припускаючи, що наближення x_n (де n – фіксоване значення к ) відомо, для знаходження x_n+1 вибираємо наступні значення a_n+1 , b_n+1 в залежності від знака добутку f(a_n ) * f(x_n ) .

Якщо f(a_n ) * f(x_n ) < 0 , то b_n+1 вважаємо рівним знайденому значенню x_n і a_n+1 рівними a_n , інакше b_n+1 = b_n , a_n+1 = x_n .

На рис. 1.1 зображена поведінка послідовних наближень у випадку ƒ(а) < 0 , ƒ(b) > 0 .

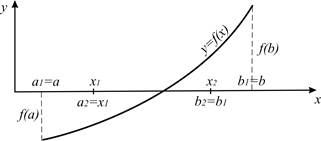
Рисунок 1.1 – Графічне зображення методу бісекцій

Рішення рівняння (1.1) вважається знайденим з точністю Е , якщо виконається умова

| х_{к + 1} – х_к | < Е (1.5)

Читайте також:

1. B. Тип, структура, зміст уроку і методика його проведення.
2. D) методу мозкового штурму.
3. Demo 11: Access Methods (методи доступу)
4. H) інноваційний менеджмент – це сукупність організаційно-економічних методів управління всіма стадіями інноваційного процесу.
5. I Метод Шеннона-Фано
6. I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
7. I. Метод єдиної подібності.
8. I. Метод рiвних вiдрiзкiв.
9. I. Органи і системи, що забезпечують функцію виділення
10. II. МЕТОДИЧНІ ВКАЗІВКИ
11. II. УЧЕБНЫЕ И МЕТОДИЧЕСКИЕ ПОСОБИЯ, ПРАКТИКУМЫ
12. III. За виділенням або поглинанням енергії

Переглядів: 801