• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Основні поняття і сутність цілочислового програмування

Цілочислове програмування – це різновид задач лінійного програмування, в якому змінні та отримані результати повинні бути цілими числами.

Задачі цілочислового програмування можуть бути лінійними, якщо обмеження і цільова функція задачі є лінійною залежністю, або нелінійними – якщо залежності будуть мати нелінійну форму.

Слід вказати, що широке використання задач цілочислового програмування в економічних дослідженнях полягає в тому, що необхідно отримувати цілочислове рішення. Цілочислове програмування виникло в 50-60-ті роки 20 століття на основі робіт Дж. Данцига і Р. Гомори.

Задача цілочислового програмування записується так :

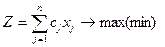, (5.1)

за умов того, що х_і є цілим числом і позитивним.

Для знаходження оптимального вирішення цілочислових задач застосовують відповідні методи. Найпростішим методом вирішення цілочислової задачі є знаходження її оптимального роз в'язку як задачі, що має лише неперервні змінні, з подальші округленням останніх.

Для знаходження оптимальних планів задач цілочислової програмування застосовують дві основні групи методів:

- методи відтинання;

- комбінаторні методи.

Основою методів відтинання є ідея поступового «звуження» області допустимих напрямів вирішення задачі. Пошук цілочислового оптимального вирішення задачі починається з розв'язування задачі з так званими послабленими обмеженнями, тобто без урахування вимог цілочисленності змінних. Далі введенням у модель спеціальних додаткових обмежень, що враховують цілочисленність змінних, багатокутник допустимих рішень послабленої задачі поступово зменшується до отримання змінних оптимального вирішення до отримання цілочислових значень. До цієї групи належать:

Ø методи розв'язування повністю цілочислових задач (дробовий
алгоритм Гомори);

Ø методи розв'язування частково цілочислових задач (другий
алгоритм Гомори, або змішаний алгоритм цілочислового програмування).

Комбінаторні методи цілочислової оптимізації базуються на повному переборі всіх допустимих цілочислових рішень, тобто вони реалізують процедуру цілеспрямованого перебору, під час якої розглядається лише частина розв’язків (досить невелика), а решта враховується одним зі спеціальних методів. Найпоширенішим у цій групі методів є метод віток і меж.

Рекомендації по формулюванню і вирішенню задач цілочислового програмування:

1. Кількість цілочисельних змінних зменшувати наскільки можливо. Наприклад, цілочисельні змінні, значення яких повинно бути не менше 20, можна розглядати як безперервні.

2. На відміну від загальних задач лінійного програмування, додавання нових обмежень, особливо включених цілочисельних змінних, звичайно зменшують час вирішення задач цілочислового програмування.

3. Якщо немає необхідності в знаходженні точного оптимального цілочисельного рішення, відмінного від безперервного рішення, наприклад, 3%. Тоді реалізацію методу гілок і меж для задачі максимізації можна закінчувати, якщо відношення різниці між верхньої і нижньої меж до верхньої межі менше 0,03.

Читайте також:

1. I. ОСНОВНІ ЕТАПИ ВИКОНАННЯ КУРСОВОЇ РОБОТИ
2. II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
3. II. Основні засоби
4. II. ОСНОВНІ ПОВНОВАЖЕННЯ ТРУДОВИХ КОЛЕКТИВІВ
5. II. Поняття соціального процесу.
6. II.3. Основні способи і прийоми досягнення адекватності
7. III. Основні обов'язки робітників та службовців
8. IV. ЗАГАЛЬНІ ПОНЯТТЯ ПРО ПЕРШУ МЕДИЧНУ ДОПОМОГУ ПОТЕРПІЛИМ.
9. IV. Основні обов'язки адміністрації
10. T. Сутність, етіологія та патогенез порушень опорно-рухової системи
11. V. ОСНОВНІ ВИМОГИ ДО ОФОРМЛЕННЯ КУРСОВОЇ РОБОТИ
12. V. Поняття та ознаки (характеристики) злочинності

Переглядів: 1395