• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Одержання коефіцієнтів лінійної регресії

Для вивченняцієї темислід досконало розібратися в попередній темі і з’ясувати концептуальні засади процесу апроксимації експериментально знайдених значень невідомої функції відгуку поліномами різного ступеня. Щоб дістати опис функції відгуку, виконують N спроб (повні факторні плани, дробові факторні плани), результати яких використовують для обчислення коефіцієнтів рівняння регресії. При цьому спочатку з’ясовують, як правило, чи можлива лінійна апроксимація функції відгуку в заданій області змінювання факторів. До поліномів вищого ступеня переходять в тому разі, коли лінійна модель не адекватна здобутим дослідним даним або потрібно глибше вивчити характер походження функції відгуку в околі деякої точки.

Рівняння лінійної регресії

. (10.1)

Коефіцієнти регресії обчислюються методом найменших квадратів. Суму квадратів відхилень розрахункових значень вихідної величини у від спостережуваних під час експерименту запишемо у вигляді

.

Слід зазначити, що останній вираз можна спростити, якщо коефіцієнт помножити на фіктивну змінну , що завжди набуває значення +1:

. (10.2)

Визначивши частинні похідні функції (10.2) і прирівнявши їх до нуля, дістанемо систему нормальних рівнянь для обчислення коефіцієнтів регресії, що забезпечують мінімум суми квадратів відхилень U:

(10.3)

де

; (10.4)

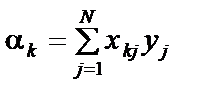
. (10.5)

Розглянемо систему нормальних рівнянь (10.3) для умов проведення повного (дробового) факторного експерименту. З урахуванням властивостей нормування та ортогональності формула для обчислення коефіцієнтів 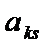спрощується (введення фіктивної змінної не порушує цих властивостей):

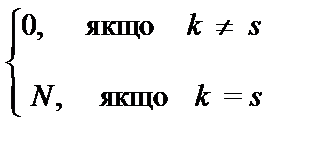
= . (10.6)

З урахуванням (10.6) систему нормальних рівнянь (10.3) можна подати у вигляді

(10.7)

Підставляючи значення з (10.5), дістанемо вираз для обчислення коефіцієнтів регресії:

. (10.8)

Зазначимо, що згідно з останнім виразом коефіцієнти лінійної регресії визначаються окремо для кожного фактора, тобто вони незалежні один від одного. Як буде показано пізніше, ця властивість є виключно важливою для оцінки впливу факторів на функцію відгуку (можна виключати чи включати різні фактори в імітаційний експеримент, залишаючи без зміни коефіцієнти регресії решти факторів.

2. Апроксимуючий поліном другого плану

Методом найменших квадратів так само можна обчислити й коефіцієнти регресії апроксимуючого полінома другого ступеня

(10.9)

Рівняння (10.9) можна записати у вигляді лінійного полінома відносно нових змінних , пов’язаних з факторами системи за правилом

Після таких перетворень коефіцієнти регресії можна знайти, якщо записати систему нормальних рівнянь (10.3) і обчислити коефіцієнти і з урахуванням нової системи невідомих.

Наприклад, поліном другого ступеня для двофакторної моделі

перетвориться до лінійного вигляду

за допомогою системи позначень

Проте для обчислення коефіцієнтів регресії полінома другого ступеня (10.9) дворівневі факторні експерименти непридатні, тому що вектори-стовпці, які відповідають змінним і в матриці планування, не відрізняються один від одного, а їхні елементи мають один і той самий рівень +1, тобто фіксуються під час експерименту. Отже, вплив кожного з факторів і окремо на функцію відгуку виявити не можна. Тому для побудови поліномів другого ступеня потрібно варіювати значення факторів принаймні на трьох рівнях.

3. Побудова композиційних планів

Оскільки до квадратних рівнянь регресії переходять, як правило, тоді, коли виявиться неадекватність лінійної апроксимації процесу, що досліджується, то з метою збереження здобутих для розрахунків лінійних коефіцієнтів регресії експериментальних даних до повного (або дробового) факторного плану додають нові точки:

нульову точку, тобто базову (центральну) точку повного чи дробового факторного плану;

«зіркові» точки, розміщені на осях кодової системи координат.

Створені таким способом плани називають композиційними. «Зіркові» точки містяться на осях координат на однаковій відстані l від центральної точки, яка називається зірковим плечем. У табл. 10.1 наведено точки композиційного плану для трьох факторів. Геометричну інтерпретацію цього плану подано на рис. 10.1, де цифрами позначені точки, в яких виконуватимуться дослідження («зіркові» точки мають номери 9 — 14).

Рис. 10.1. Геометрична інтерпретація композиційного плану (n = 3)

Значення зіркового плеча l обчислюється залежно від обраного критерію оптимальності композиційного плану. При побудові квадратних поліномів найчастіше використовуються два критерії оптимальності: ортогональність і рототабельність.

Композиційний план, вектори-стовпці матриці планування якого ортогональні, називається ортогональним центральним композиційним планом.Властивість ортогональності планів дуже істотна, оскільки дає змогу, як уже зазначалось, визначати коефіцієнти регресії незалежно один від одного. Це означає, що матриця коефіцієнтів 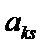системи нормальних рівнянь (10.3) при ортогональності плану має діагональний вигляд.

Матриця планування ортогоналізується перетворенням квадратичних членів

(10.10)

У цьому разі вектор-стовпець фактора буде ортогональним до векторів-стовпців, які відповідають факторам , тобто

З урахуванням перетворення (10.10) поліном (10.9) запишеться у вигляді

Значення зіркового плеча l обирається з умови ортогональності векторів-стовпців і матриці планування:

(10.11)

Підставивши у (10.11) вираз (10.10) і виконавши перетворення, дістанемо біквадратне рівняння для визначення зіркового плеча

Читайте також:

1. Алгоритм розрахунку основних фінансових показників (коефіцієнтів)
2. Аналіз коефіцієнтів цільової функції
3. Аналіз одержання результатів. Висновки рекомендації.
4. Аналіз фінансових коефіцієнтів.
5. Аналіз фінансової звітності методом коефіцієнтів
6. Антимонопольний комітет України здійснює контроль за додержанням суб'єктами зовнішньоекономічної діяльності законодавства про захист економічної конкуренції.
7. Багатомірна лінійна модель регресії.
8. Безрозмірною характеристикою гідротрансформатора називається залежність коефіцієнтів пропорційності моментів насосного і турбінного коліс від його передаточного відношення.
9. Біном Ньютона. Трикутник Паскаля. Властивості біноміальних коефіцієнтів
10. Біотехнологія одержання антибіотиків
11. Біотехнологія одержання ІНТЕРФЕРОНІВ
12. Вибір виду рівняння регресії. Регресійний аналіз

Переглядів: 906