• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Ортогональний центральний композиційний експеримент

Композиційний план, вектори-стовпці матриці планування якого ортогональні, називається ортогональним центральним композиційним планом.Властивість ортогональності планів дуже істотна, оскільки дає змогу, як уже зазначалось, визначати коефіцієнти регресії незалежно один від одного. Це означає, що матриця коефіцієнтів 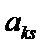системи нормальних рівнянь (10.3) при ортогональності плану має діагональний вигляд.

Матриця планування ортогоналізується перетворенням квадратичних членів

(10.10)

У цьому разі вектор-стовпець фактора буде ортогональним до векторів-стовпців, які відповідають факторам , тобто

З урахуванням перетворення (10.10) поліном (10.9) запишеться у вигляді

Значення зіркового плеча l обирається з умови ортогональності векторів-стовпців і матриці планування:

(10.11)

Підставивши у (10.11) вираз (10.10) і виконавши перетворення, дістанемо біквадратне рівняння для визначення зіркового плеча

(10.12)

Зазначимо, що ця формула справджується для випадку, коли ортогональний композиційний план здобуто додаванням зіркових точок до повного факторного плану при однаковій кількості дублюючих (паралельних) спроб для всіх точок плану. Якщо число таких спроб різне, то за допомогою співвідношення (10.11) можна дістати рівняння для обчислення зіркового плеча, вважаючи кожну дублюючу спробу новою точкою композиційного плану.

Читайте також:

1. II етап. Емпіричне обслідування та експеримент.
2. Банківська система в ринковій економіці є звичайно дворівневою і включає центральний банк (емісійний) і комерційні (депозитні) банки різних видів.
3. В.О. Сухомлинський — майстер унікального експерименту
4. Види експериментального методу
5. Види експериментів
6. Відповідь: експериментальний фактор (змінна)
7. Влада – центральний компонент політичної системи.
8. Вплив експериментатора на результати дослідження. Способи контролю.
9. Всеукраїнський Центральний Виконавчий Комітет
10. Гіпотези, які не відхиляються в експерименті, перетворюються на компоненти теоретичного знання про реальність: факти, закономір­ності, закони.
11. До основних методів психології належать: спостереження, опитування і експеримент.
12. Досліджуваний, його діяльність в експерименті. Види досліджуваних.

Переглядів: 967