• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Визначення числових характеристик розподілу ймовірностей цих результатів як випадкових величин

Числові характеристики розподілу ймовірностей результатів вимірювання обчислюють для виправленого ряду результатів вимірювань, тобто ряду, з якого усунені грубі похибки. При цьому слід здійснити наступні операції:

- вирахувати математичне сподівання (середнє арифметичне) виправлених результатів спостережень і прийняти його за результат вимірювання, а також моду та медіану;

- вирахувати згідно з ГОСТ 11.004-74 оцінку середнього квадратичного відхилення результату спостереження (див. табл. 2 додатку) та оцінку середнього квадратичного відхилення результату вимірювання [4].

- вирахувати оцінки другого m₂, третього m₃ та четвертого m₄ центральних моментів розподілу, оцінки характеристик асиметрії 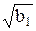і гостровершинності 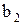розподілу.

Оцінкою математичного сподівання m_x є середнє арифметичне цього ряду 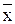, яке надалі вважають результатом вимірювання .

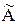Оцінкою медіани 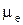при непарному числі n результатів вимірювань є середній член варіаційного ряду з порядковим номером 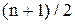, тобто:

;

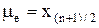а при парному числі n результатів вимірювань – середнє арифметичне між членами цього ряду з порядковими номерами 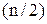та :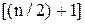

.

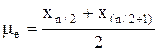Оцінкою моди 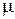є результат вимірювання, який найчастіше зустрічається в даному ряді. У деяких випадках доцільно групувати дані за інтервалами частот однакової довжини. При цьому мода береться як центральна точка частотного інтервалу, який вміщає в собі найбільше число вимірювань.

Оцінка дисперсії 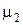або 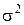обчислюється наступним чином:

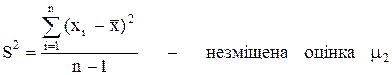
m₂ є одночасно оцінкою центрального моменту розподілу другого порядку.

Відповідно оцінки центральних моментів розподілу третього m₃ і четвертого m₄ порядків вираховуються за формулами:

; .

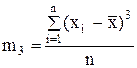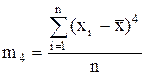Оцінка 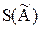середнього квадратичного відхилення результатів вимірювань визначається за формулою:

.

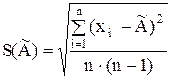Оцінка S₁ середнього квадратичного відхилення результатів спостережень визначається як 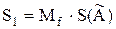, де коефіцієнт 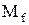в залежності від числа ступенів вільності f=n-1 вибирається з таблиці 2 у додатку.

Оцінки характеристик асиметрії 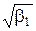і ексцесу 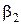(гостро- чи плосковершинності) розподілу, які позначаються відповідно 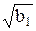і 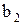, дорівнюють:

; .

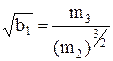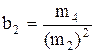Читайте також:

1. A) Оцінка захисних споруд за ємністю – визначення коефіцієнта Квм.
2. CMM. Визначення моделі зрілості.
3. I визначення впливу окремих факторів
4. I. Доповнення до параграфу про точкову оцінку параметрів розподілу
5. I. Загальна характеристика політичної та правової думки античної Греції.
6. II. Визначення мети запровадження конкретної ВЕЗ з ураху­ванням її виду.
7. II. ВИРОБНИЧА ХАРАКТЕРИСТИКА ПРОФЕСІЇ
8. II. Морфофункціональна характеристика відділів головного мозку
9. II. Мотивація навчальної діяльності. Визначення теми і мети уроку
10. II. Обробка результатів
11. III етап. Опрацювання результатів дослідження.
12. III. Економічна інтерпретація результатів статистичного дослідження банків

Переглядів: 512