- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Приклад
Необхідно здійснити опрацювання результатів спостережень, а саме:
1. Виявити та усунути з ряду результатів спостережень промахи.
2. Вирахувати результат вимірювання та оцінки середнього квадратичного відхилення результату спостереження та вимірювання.
3. Перевірити належність результатів вимірювань до нормального розподілу за допомогою складового критерію та методики Пірсона.
4. Вирахувати довірчі межі випадкової похибки вимірювання ПВП.
При вимірюванні температури t були отримані наступні результати, °С
| № п/п | |||||||||||||||||
| t,°С | 20,42 | 20,43 | 20,40 | 20,41 | 20,43 | 20,42 | 20,41 | 20,39 | 20,30 | 20,40 | 20,44 | 20,43 | 20,42 | 20,41 | 20,39 | 20,41 | 20,40 |
1. Для виявлення в результатах вимірювання фізичних величин грубих похибок (промахів) їх необхідно розташувати в порядку зростання або спадання, тобто утворити варіаційний ряд:
| S17 | *2 | *3 | *4 | *3 | *3 | ||
| № п/п | 2-3 | 4-6 | 7-10 | 11-13 | 14-16 | ||
| № досл | 8,15 | 3,10,17 | 4,7,14,16 | 1,6,13 | 2,5,12 | ||
| t,°C | 20,30 | 20,39 | 20,40 | 20,.41 | 20,42 | 20,43 | 20,44 |
| Dt,°C | -0,106 | -0,016 | -0,006 | 0,004 | 0,014 | 0,024 | 0,034 |
| Dt2 | 0,01124 | 0,000256 | 0,000108 | 0,000016 | 0,000196 | 0,000576 | 0,001156 |
Середнє арифметичне значення температури:
Незміщена оцінка середньоквадратичного відхилення результатів вимірювання:
Для довірчої ймовірності Р=95% і числа спостережень n=17 (f=n-1=16) з таблиці 1 знаходимо r¢=2,577.
Для сумнівного 1-го (9-го) результату:
r1=3,354 > r¢=2,577 – перевищує допустиме значення
Для сумнівного 17-го (11-го) результату:
r17=1,076 < r¢=2,577 – не перевищує допустиме значення
Отже, 1-й результат t=20,30°C є грубою похибкою і його виключаємо.
Після цього вираховуємо нові значення оцінок параметрів розподілу:
| S=16 | *2 | *3 | *4 | *3 | *3 | |
| №п/п | 1-2 | 3-5 | 6-9 | 10-12 | 13-15 | |
| №досл | 8, 15 | 3, 10, 17 | 4, 7, 14, 16 | 1 ,6, 13 | 2, 5, 12 | |
| t,°C | 20,39 | 20,40 | 20,41 | 20,42 | 20,43 | 20,44 |
| Dt | -2,3*10-2 -4,6*10-2 | -1,3*10-2 -3,9*10-2 | -0,3*10-2 -1,2*10-2 | 0,7*10-2 2,1*10-2 | 1,7*10-2 5,1*10-2 | 2,7*10-2 2,7*10-2 |
| Dt2 | 5,29*10-4 10,58*10-4 | 1,69*10-4 5,07*10-4 | 0,09*10-4 0,36*10-4 | 0,49*10-4 1,47*10-4 | 2,89*10-4 8,67*10-4 | 7,29*10-4 7,29*10-4 |
| Dt3 | -12,67*10-6 -24,334*10-6 | -2,197*10-6 -6,591*10-6 | -0,027*10-6 -0,108*10-6 | 0,343*10-6 1,029*10-6 | 4,913*10-6 14,739*10-6 | 19,683*10-6 19,683*10-6 |
| Dt4 | 27,9841*10-8 55,9682*10-8 | 2,8561*10-8 8,5683*10-8 | 0,0081*10-8 0,0324*10-8 | 0,2401*10-8 0,7203*10-8 | 8,3521*10-8 25,0563*10-8 | 53,1441*10-8 53.1441*10-8 |
Середнє арифметичне значення температури:
.
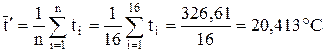Незміщена оцінка середньоквадратичного відхилення результатів вимірювання:
.
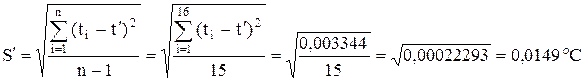Найбільше відрізняється від нового середнього 
16-ий результат 
.
Для сумнівного 16-го (11-го) результату:
.
З таблиці 1 для n=16 (f=16-1=15) i P=95% знаходимо r¢=2,551 > r16=1,80. Отже, 16-й результат і тим більше всі інші результати не є грубими похибками і вони залишаються в ряді результатів.
У зв’язку з тим, що S¢ є меншим від попереднього значення S в 2 рази, то і розсіювання результатів практично в 2 рази стало меншим.
.
2. Вважаємо, що ряд значень вимірювання є виправленим і результатом вимірювання температури є його середнє арифметичне 
.
Медіана 
, мода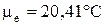 
.
Оцінка середнього квадратичного відхилення 
результатів вимірювань вираховується за формулою:
.
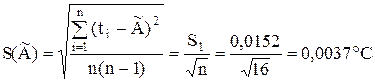Оцінка середнього квадратичного відхилення результату s спостережень вираховується за формулою:
;
Для f=n-1=15 з таблиці 2: Mf=1,017, отже S1=1,017*0,0037=0,00376°C.
Оцінка дисперсії:
незміщена 
4;
зміщена 
.
3. Перевіримо гіпотезу про те, що результати спостережень належать до нормального розподілу згідно із складовим критерієм.
Критерій 1
Вираховуємо зміщену оцінку середньоквадратичного відхилення результатів вимірювання:
;
Обчислюємо відношення:
.
З таблиці 3 для n=16 i P=95% отримуємо значення квантілів розподілу 
; 
.
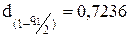Перевіряємо виконання умови: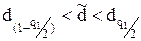 
,
0,7236 < 0,8485 < 0,8884
Умова виконується, отже робимо висновок, що результати спостережень згідно з критерієм 1 розподілені нормально.
Критерій 2
Незміщена оцінка середнього квадратичного відхилення 
.
З таблиці 4 для n=16 i q2=5% (РД=95%) отримуємо m=1; P=0,98;
Знаходимо верхній квантіль розподілу нормованої функції Лапласа при p/2=0,98/2=0,49.
Для Фо(z)=0,4900 знаходимо 
.
Допустиме значення різниці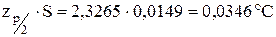 
.
Кількість різниць, яка перевищує значення 
повинна бути 
.
Найбільша з різниць дорівнює 
.
Як бачимо жодна з різниць не перевищує значення 0,0346°С. Отже результати спостережень згідно з критерієм 2 розподілені нормально.
Оцінки центральних моментів розподілу другого m2, третього m3 і четвертого m4 порядків вираховуються за формулами:
;
; 
.
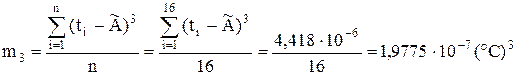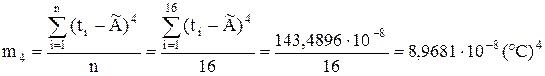Оцінки характеристик асиметрії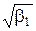 
і ексцесу 
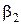(гостро- чи плосковершинності) розподілу, які позначаються відповідно 
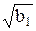і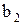 
, дорівнюють:
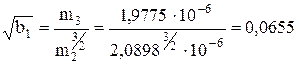>0 асиметрія додатна, розподіл правосторонній
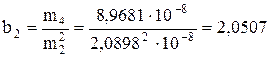<3 розподіл плосковершинний.
Методика Пірсона:
Для того, щоб перевірити з допомогою методики Пірсона, чи результати вимірювань належать до нормального розподілу, додатково необхідно вирахувати дисперсії характеристик асиметрії 
та ексцесу D(b2), які відповідно визначаються:
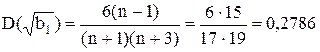
і перевірити виконання наступних умов:
;
;
;
.
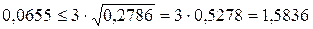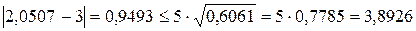Як бачимо ці умови виконуються, отже робимо висновок що результати вимірювань належать до нормального розподілу.
4 Випадкова складова похибки результату вимірювання визначається за формулою:
.
де t – коефіцієнт Ст’юдента.
За таблицею 5 для заданих числа f=n-1=15 ступеня вільності та довірчої ймовірності Pд=95% знаходимо 
.
Отже 
.
Таким чином результат вимірювання температури запишеться: 
.
Читайте також:
- IV. ПРИКЛАДИ ТИПОВИХ ІНДИВІДУАЛЬНИХ ЗАВДАНЬ ТА ПОРЯДОК ЇХ РОЗВ’ЯЗАННЯ
- Абсолютні синоніми (наприклад, власне мовні й запозичені) в одному тексті ділового стилю вживати не рекомендується.
- Алгоритм однофакторного дисперсійного аналізу за Фішером. Приклад
- Аналіз структури та динаміки необоротних активів за даними Ф№1 «Баланс» (на прикладі ВАТ «Горизонт»)
- Базові та прикладні класифікації
- В Додатку до диплома (приклад)
- В процесі читання виділіть маркером або підкресліть приклади дії променів на живі організми.
- В чому полягає явище тунелювання через потенціальний бар’єр, наведіть приклади.
- Вивчення прикладу СК: моніторинг дотримання положень КПК ООН з боку СК
- Визначення і приклади
- Виокремте з обраної програми концептуальну ідею, мету, наведіть 1-2 приклади форм і методів її реалізації.
- Вільсон О. Г. Охорона праці в галузі (на прикладі будівництва). Навчальний посібник. – К.: «Основа». 2006. – 204 с.
| <== попередня сторінка | | | наступна сторінка ==> |
| Вирахування довірчих меж випадкової похибки результату вимірювання | | |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |