Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Дидактичні умови формування предметної компетентності старшокласників у процесі вивчення предметів фізико-математичного циклу

Особливе місце у формуванні предметної компетентності старшокласників займають дидактичні умови, які позитивно впливають на їхній інтелектуальний рівень, удосконалення навчальної діяльності, самореалізацію, сприяють різносторонньому розвиткові особистості, що є соціальною потребоюсуспільства.

У практиці, як і вматематиці, розрізняють необхідні і достатні умови. У педагогічному словнику [166] необхідні і достатні умови трактуються наступним чином: необхідні умови ефективного функціонування будь– якої системи –це умови, без яких вона не може працювати повною мірою: достатні умови–це умови для нормальної роботи будь–якої системи.

Використовуючи термін «дидактичні умови», ми будемо дотримуватися його значення, пов’язаного з процесом формування предметної компетентності старшокласника, який навчається за визначеною сукупністю умов.

Аналіз практики свідчить про те, що формування предметної компетентності відбувається послідовно, шляхом використання спеціальних методик, методів та застосування новітніх педагогічних технологій.

Оскільки процес формування досліджуваної компетентності вимагає певної спiльної діяльностi вчителя й учнів, важливе місце вiдводиться оптимальному застосуванню та формуванню дидактичних умов.

У науковій літературі існують різні погляди на визначення таких понять: «умова» та «дидактична умова», «педагогічна умова» . Що саме розуміють науковці під цими поняттями.

У словниках визначається, «умова» - це «вимога, що висувається однією із сторін; як усний або письмовий договір про що-небудь; як правила, встановлені в будь-якій сфері життя, діяльності; як обставини, за яких відбувається що-небудь» [160, с. 776]; «місце, у якому здійснюється що-небудь, обставину, при якій відбувається що-небудь; обов’язкові обставини, передумови, що визначають, зумовлюють існування чого-небудь» [71, с. 870–871];– «необхідну обставину, яка робить можливим здійснення, створення чого-небудь або сприяє чомусь» [212, т. 10, с. 442]; в енциклопедичному словнику поняття «умова» розглядається як «сукупність чинників, що впливають на кого-небудь, що-небудь, що створюють середовище, в якому відбувається щось. Умова характеризує постійні чинники суспільного, побутового та іншого оточення» [215, с. 625]. У словнику з освіти та педагогіки поняття «умова» трактується як «сукупність змінних природних, соціальних, зовнішніх і внутрішніх впливів, що діють на фізичний, психологічний, моральний розвиток людини, її поведінку, виховання, навчання, формування особистості» [173, с. 36]. У філософському словнику умова – це категорія, яка відбиває загальні відношення речі до тих факторів, які її породжують і завдяки яким вона існує [233, с. 703].

У педагогіці термін «умова» використовується з метою характеристики педагогічного процесу. Вчені активно досліджують вплив різних умов на навчальний процес. Проте єдиного твердження вони ще не дійшли, існують різні точки зору на розуміння поняття «умова навчання», зокрема «дидактична умова».

Так, дослідниця А. Багдуєва зазначає, що педагогічні умови є обставинами навчально-виховного процесу, цілеспрямовано відібрані і призначені для конструювання і застосування змісту, форм, методів, навчального процесу з метою досягнення мети навчання [11, с. 12]. О. Луганцева під педагогічними умовами розуміє спеціально організовані педагогічні обставини (сукупність заходів), які сприяють підвищенню ефективності, посилюючи ефект процесу підготовки, тобто такі, що чинять позитивний вплив на його вдосконалення [131, c. 111].

І. Аксаріна зазначає, що педагогічні умови є «сукупністю об’єктивних можливостей змісту, форм, методів і прийомів підвищення ефективності навчально-виховного процесу і матеріально-просторового середовища, що забезпечують успішне вирішення поставлених і проектованих у дослідженні завдань». Ось чому до педагогічних умов можна віднести свідомо створені обставини освітнього процесу, які здатні забезпечувати ефективне та продуктивне протікання цього процесу [2, с. 12].

Ю. Корницька визначає педагогічні умови як спеціально створені й запроваджені в педагогічну практику фактори, які сприяють вихованню студентів [113, c. 112]. Тобто спеціально створені педагогічні умови можуть впливати як на процес навчання, так і на процес виховання. Різні умови впливають на процес навчання по-різному, та діють лише в певних ситуаціях, є специфічними для усіх учасників навчального процесу. Це можуть бути обставини, фактори, правила, вимоги до організації і змісту педагогічного процесу.

Таким чином, аналіз вивчених праць зазначених вчених дає підстави говорити, що дослідники по-різному розуміють та трактують поняття «педагогічні умови», розглядаючи їх як:

- опис педагогічного середовища;

- деякі обставини, безпосередньо необхідні для перебігу педагогічного процесу;

- фактори, шляхи, напрямки педагогічного процесу;

- прогнозовані результати навчального процесу;

- форми, методи, прийоми навчання [224].

Шкільна практика показує, що педагогічні умови представлені трьома складниками процесу навчання: учень - учитель - узгоджені дії учня і вчителя у цілісному навчально-виховному процесі. На нашу думку, «педагогічні умови» мають бути націлені на підтримку психологічного комфорту, на розвиток когнітивних, емоційних і вольових процесів дитини, на заохочення творчої активності старшокласників.

Використовуючи термін «педагогічні умови» ми будемо дотримуватися його значення, пов’язаного з процесом формування предметної компетентності старшокласника, який буде навчатися за визначеною сукупністю умов.

Педагоги обґрунтовують різноманітні дидактичні умови, які позитивно впливають на процес навчання.

Аналізуючи значення термін дидактична умова, науковець Л. Перетяга визначає його походження з «філософського розуміння умов як відношення предмета до навколишніх явищ, без яких неможливе його існування». Відносно процесу навчання дидактичні умови слід розглядати як вимоги, обставини, які зумовлюють й ініціюють процес його розвитку [167, с. 234].

Специфічною рисою поняття "дидактичні умови" є те, що воно включає в себе елементи всіх складових процесу навчання: мету, зміст, методи, форми, засоби. Ю. К. Бабанський виділяє такі педагогічні умови ефективності навчально-виховного процесу: методологічна і теоретична підготовка вчителів; створення певної бази (підготовка та створення навчально-методичної літератури, технічних засобів, наочних посібників); морально-психологічні умови [10, с. 321-325.]. Тобто, «дидактичні умови» – це умови, за яких компоненти навчального процесу представлені в найкращому взаємовідношенні, що дає можливість вчителю плідно керувати навчальним процесом, а учням успішно навчати.

Таким чином, під дидактичними умовами, які сприяють формуванню предметної компетентності старшокласників у процесі вивчення предметів фізико-математичного циклу, будемо розуміти обставини процесу навчання, що є результатом цілеспрямованого вибору, конструювання та застосування елементів змісту, методів, форм навчання фізики й математики, завдяки яким процес може бути успішним.

З метою виявлення й теоретичного обґрунтування дидактичних умов ефективного формування предметної компетентності старшокласників у процесі вивчення фізико-математичних дисциплін уточнимо визначення та структуру предметної компетентності.

Дидактичним умовам навчання присвячено низку досліджень дидактів, психологів, учителів-практиків. (Н.Д.Майбородюк, Л. В. Осіпа, С. Рубінштейн, О. Леонтьєв, Л. Божович, О. Дусавицький та інші).

Як зазначено в І розділі, що предметна компетентність – набутий учнями у процесі навчання досвід специфічної для певного предмета діяльності, пов’язаної із засвоєнням, розумінням і застосуванням нових знань. До складу предметної компетентності в процесі вивчення фізико-математичних дисциплін ми виділили такі компоненти: мотиваційний, когнітивний, діяльнісний та особистісний.

Наукові дослідження з проблем формування компетентностей старшокласників, означення й структури предметної компетентності, а також результатів констатувального етапу експерименту дають підстави для виокремлення дидактичних умов для фрмування предметних компетентностей у старшокласників у процесі вивчення фізики й математики.

Н.Єрмакова, розглядаючи педагогічні умови розвитку предметної компетентності в учнів основної та старшої школи, виділяє такі:

– забезпечення різноманітності форм організації навчально-пізнавальної діяльності школярів у період практики;

– застосування завдань, які виконуватимуть школярі мають носити практичний, прикладний, життєвий та профорієнтаційний характер;

– надання можливості учню обирати той вид діяльності, який йому подобається і надасть можливість розкрити свої здібності;

– ознайомлення вчителів з метою, завданнями та основними функціями навчальної практики з фізики [72].

Є.Дібрівна, досліджуючи формування математичної компетентності майбутніх аграріїв, виділяє такі організаційно-педагогічні умови:

– забезпечення професійно-прикладної спрямованості навчання;

– реалізація інформаційно-методичного забезпечення усіх рівнів та форм математичної освіти;

– інтеграція у викладанні математичних та загальноінженерних дисциплін;

– створення викладачем позитивного емоційного фону на основі навчальних ситуацій [63].

І.Рябуха зазначає, що необхідними умовами соціальної компетентності ліцеїстів є:

– розвивальне середовище;

‒ сприятливий клімат;

‒ суб’єкт-суб’єктна взаємодія;

– зворотний зв'язок [187].

С.Раков в соєму дослідженні зазначає, що для формування математичних

компетентностей необхідною умовою є використання інформаційно-комунікаційні технології[179].

У нашому дисертаційному дослідженні при визначенні дидактичних умов формування предметної компетентності старшокласників у процесі вивчення фізико-математичних дисциплін ураховувалися особливості такої підготовки, а саме: зміст предметної компетентності; наукові підходи до формування цієї компетентності; мотиваційний, когнітивний, особистісний та діяльнісний компоненти формування компетентності старшокласників; умови формування знань з математики й фізики.

Усе вищезгадане дало можливість стверджувати, що формування предметної компетентності старшокласників у процесі вивчення математики й фізики забезпечує сукупність таких дидактичних умов:

· створення позитивної мотивації старшокласників до навчально-пізнавальної діяльності, спрямованої на формування предметної компетентності у процесі вивчення фізики й математики;

· використання широкого спектру прикладних задач в контексті реалізації компетентнісного підходу;

· застосування інформаційно-комунікативних технологій на уроках фізико-математичного циклу;

Вважаємо, що перераховані дидактичні умови логічно й тісно пов’язані між собою і кожна з них є необхідною й достатньою для ефективного формування предметної компетентності старшокласників в процесі вивчення фізики й математики.

Розглянемо детально кожну із вказаних вище дидактичних умов.

Створення позитивної мотивації старшокласників до навчально-пізнавальної діяльності, спрямованої на формування предметної компетентності у процесі вивчення математики й фізики. Мотивація має важливе значення в процесі формування предметної компетенції, бо вона грунтується переважно на самостійній діяльності.Відомо, що навчальна діяльність здійснюється під впливом певних стимулів, спонукань, якими є потреби, інтереси, переконання, ідеали, ціннісні орієнтації тощо. Ці стимули впливають на формування змісту діяльності, в якій вони реалізуються, оскільки зумовлюють, на думку психологів, мотивацію (або мотиваційну сферу) навчальної діяльності. Рівень сформованості мотивації є необхідною передумовою успіху навчальної діяльності. Зрозуміло, що персональний вектор розвитку кожного учня не завжди збігається з напрямом руху у велику науку. Але із задоволенням і користю вчитися здатні всі. Для цього процес навчання має бути сконструйований і важливим місцем у роботі вчителя є формування мотивації навчання в учнів. Бо якщо в учнів є бажання й інтерес до навчання, то вони можуть реалізувати свої здібності у вивченні різних предметів, будуть зацікавлені у їх вивченні.

Поняття «мотивація» у словнику практичного психолога тлумачиться як сукупність мотивів, які спонукають до дії [44] івикористовується у сучасній психології у двоякому розумінні: визначення системи факторів, детермінуючих поведінку, і характеристика процесу, який стимулює і підтримує поведінкову активність на певному рівні.

У сучасному словнику-енциклопедії (УСЕ) [230], слово «мотивація» трактується так:

- психічний регулюючий механізм, який приводить в дію механізм поведінки особи і скеровує її на досягнення визначеної мети;

- стан внутрішнього напруження, який спонукає особу до дії, що робить можливою зменшення цього напруження;

- відносно тривала тенденція прагнення до досягнення визначеної мети;

– може мати свідомий чи підсвідомий характер.

В. Вілюнас відзначає, що мотивація – це сукупна система процесів, які відповідають за спонукання та діяльність [32].

Серед психологів початку ХХ століття, які порушували питання щодо мотивації людської поведінки, визначають О. Лазурського, М. Ланге,
Л. Виготського, Д. Узнадзе та інших, які довгі роки проводили дослідження, спрямовані в основному на вивчення пізнавальних процесів. Із створених у 60-ті роки ХХ ст. концепцій мотивації, більш-менш продуманою та доведеною до певного рівня закінченості вважається тільки створена О. Леонтьєвим теорія діяльнісного походження мотиваційної сфери людини [84,с.230-235].

Так за О. Леонтьєвим, мотивація - це циклічний процес безперервного взаємного впливу та перетворень, у якому суб'єкт дії та ситуація взаємно впливають одне на одного і результатом якого є реально простежена поведінка [125]. Вона пояснює цілеспрямованість дії, організованість та стійкість цілісної діяльності, спрямованої на досягнення окремої цілі.

Проведений нами аналіз свідчить, що вченими визначено, що найдієвішими масовими спонуками в навчанні учнів є мотиви,

Мотив на відміну від мотивації - це те, що належить самому суб'єкту поведінки, є його стійкою особистою властивістю [100,с.11]. Мотивація є більш широким поняттям, ніж мотив.

На думку Л. Столяренко: «Мотив - це збудження до діяльності, пов'язане з задоволенням потреби суб'єкта»[15,с.12-15]. Під мотивом також найчастіше розуміють причину, яка лежить в основі вибору дій і вчинків, сукупності зовнішніх і внутрішніх умов, що викликають активність суб'єкта[15,с.12-15]. Мотив також можна визначити як поняття, що в узагальнюючому вигляді являє собою багато диспозицій. З усіх можливих диспозицій найбільш важливим є поняття «потреби». Її ще називають станом «нужди» людини в окремих умовах, які необхідні для нормального існування та розвитку. У людини, крім фізичних та органічних потреб, є ще матеріальні, духовні, соціальні. Потреби - динамічно активні стани особистості, що виявляють її залежність від конкретних умов існування і породжують діяльність спрямовану на зняття цієї залежності [27,с.45]. В процесі діяльності відбувається як розвиток особистості, так і перетворення середовища, в якому живе людина. Отже, потреби - це рушійна сила розвитку особистості. Мотиви, потреби та цілі - є складовими мотиваційної сфери людини.

Проблеми мотивації навчання школярів досліджуються Ю. Бабанським, А. Марковою, М. Матюхіною, О. Малихіною та іншими.

Навчальна мотивація визначається як частковий вид мотивації, включений в певну діяльність, - в даному випадку діяльність учіння. Як підкреслює провідний психолог, що займається вивченням мотивації учбової діяльності, А. Маркова: «Становлення мотивації є не просте зростання позитивного або посилювання негативного відношення до учіння, а ускладнення структури мотиваційної сфери, що стоїть за ним, вхідних в неї спонук» [137]. Тому, аналізуючи мотивацію учбової діяльності, головне не тільки визначити домінуючий мотив, а й враховувати усі структури мотиваційної сфери людини.

В. Апельт виділив наступні мотиви учіння: соціальні (обов'язок і відповідальність, розуміння соціальної значущості учіння, прагнення зайняти певну позицію у відношенні з тими, що оточують, дістати їх схвалення); пізнавальні (орієнтація на оволодіння новими знаннями, закономірностями, орієнтація на засвоєння способів добування знань); комунікативні (спілкування з однолітками, дорослими); і мотиви саморегуляції (орієнтація на придбання додаткових знань і потім на побудову спеціальної програми самовдосконалення) [4,с.162].

А. Хуторський виділяє такі види мотивації: пізнавальна, особистісна, мовна, соціальна, комунікативна, економічна, ділова [243].В. Кухаренко відзначає, що чим вищий рівень мотивації, тим вищими є результати діяльності. Він також вказує на те, что «сильні» та «слабкі» учні відрізняються не стільки рівнем інтелекту, скільки рівнем мотивації навчальної діяльності. У «сильних» учнів переважає внутрішня мотивація, а у «слабких» – зовнішня. Мотивація здатна частково компенсувати недостатній об’єм знань, умінь і навичок та наявність необхідних здібностей. У той же час відсутність мотивації не може компенсуватися рівнем знань.

На думку П. Якобсона типи мотивації, пов'язаної з результатами учіння, мають бути такими:

1. Мотивація, яка умовно може бути названа «негативною».

Під негативною мотивацією Якобсон має на увазі спонуки школяра, викликані усвідомленням певних незручностей і неприємностей, які можуть виникнути, якщо він не вчитиметься (докори з боку батьків, вчителів, однокласників). Така мотивація не приводить до успішних результатів;

2. Мотивація, що має позитивний характер, але так само пов'язана з мотивами, закладеними поза самою діяльністю.

Ця мотивація виступає в двох формах. У одному випадку така позитивна мотивація визначається вагомим для особи соціальним устремлінням (відчуття обов'язку перед близькими). Інша форма мотивації визначається вузькоособистими мотивами: схвалення тих, що оточують, шляхи до особистого благополуччя.

3. Мотивація, яка лежить в самій учбовій діяльності (мотивація, пов'язана безпосередньо з цілями учіння, задоволення допитливості, подолання перешкод, інтелектуальна активність) [31,с.195].

Отже, навчальна мотивація, як і будь-яка інша, є системним, ієрархічно структурованим утворенням і характеризується спрямованістю, стійкістю та динамічністю. Вона ґрунтується на потребі - психічному стані, що характеризується пізнавальною активністю дитини, її готовністю до засвоєння знань.

У чисельних дослідженнях обґрунтовується необхідність створення спеціальних умов виникнення розвитку в дитини інтересу до учіння, до вчителя. На основі системного аналізу виділено основні умови, що сприяють розв'язанню цієї задачі.

Можливість створення умов виникнення інтересу до вчителя, до навчання (як емоційного переживання задоволення пізнавальної потреби) і формування самого інтересу наголошувалася багатьма дослідниками. На основі системного аналізу були сформульовані основні чинники, сприяючі тому, щоб навчання було цікавим для школяра [5, с.451-450]. Згідно даних цього аналізу, найважливішою передумовою створення інтересу до навчання є виховання широких соціальних мотивів діяльності, розуміння її сенсу, усвідомлення важливості процесів, що вивчаються, для власної діяльності.

Спираючись на дані дослідження, вважаємо, що необхідною умовою для створення в учнів інтересу до змісту навчання і до самої учбової діяльності – це можливість проявляти в навчанні розумову самостійність і ініціативність. Зробити це вчителі зможуть,застосовуючи активні методи навчання. При цьому основним засобом виховання стійкого інтересу до навчання - використання таких питань і завдань, вирішення яких вимагає від учнів активної пошукової діяльності.

Основна діяльність вчителів – це урок. Ефективним урок буде тоді, коли в учня виникло бажання розуміти, вивчати новий матеріал, з’явилась зацікавленість роботою, коли він стає співучасником навчально-виховного процесу. Тому вважаємо, що велику роль у формуванні інтересу до навчання відіграє створення проблемної ситуації на уроках, зіткнення учнів з трудністю, яку вони не можуть вирішити за допомогою запасу знань, що є у них; стикаючись з трудністю, вони переконуються в необхідності отримання нових знань або застосування старих в новій ситуації. Цікава тільки та робота, яка вимагає постійної напруги. Легкий матеріал, що не вимагає розумової напруги, не викликає інтересу. Подолання труднощів в учбовій діяльності - найважливіша умова виникнення інтересу до неї. Складність учбового матеріалу й завдання призводить до підвищення інтересу тільки тоді, коли ця трудність посильна, переборна, інакше інтерес швидко падає.

Учбовий матеріал і прийоми учбової роботи повинні бути достатньо різноманітні. Різноманітність забезпечується не тільки зіткненням учнів з різними об'єктами в ході навчання, але і тим, що в одному і тому ж об'єкті можна відкривати нові сторони. Новизна матеріалу - найважливіша передумова виникнення інтересу до нього. Проте, пізнання нового повинно спиратися на знання, що вже є у школяра. Використання раніше засвоєних знань - одна з основних умов появи інтересу. Істотний чинник виникнення інтересу до учбового матеріалу - його емоційне забарвлення, живе слово вчителя. Ці положення, сформульовані С.Бондаренком [23], можуть служити певною програмою організації учбового процесу, спеціально направленою на формування інтересу.

Великий, але неоднозначний вплив на навчання здійснює потреба в спілкуванні і домінуванні. Проте для самої діяльності особливо важливі мотиви інтелектуально-пізнавального плану. Керуючись подібними мотивами, не зважаючи на втому, час, протистоячи іншим спонукачам і відволікаючим чинникам, учень наполегливо і захоплено працює над учбовим матеріалом, над вирішенням учбової задачі. Тут важливий висновок був отриманий Е.Ільїним - "найбільший вплив на шкільні успіхи надає пізнавальна потреба у поєднанні з високою потребою в досягненнях" [96,с.23].

Отже, для створення позитивної мотивації старшокласників до навчально-пізнавальної діяльності, спрямованої на формування математичної компетентності необхідно:

– пробуджувати в учнів розумову самостійність, ініціативність в урочній та позаурочній діяльності;

– застосовувати активні форми та методи навчання;

– здійснювати активізацію пізнавальної діяльності учнів у навчальному процесі за допомогою проблемних ситуацій, ситуацій зацікавленості, вільного вибору учнями навчальних завдань, ситуацій успіху тощо;

– забезпечити різноманітність навчального матеріалу та прийомів учбової роботи.

Таким чином, становлення особистості відбувається через формування мотивації стати особистістю. Тому кожен педагог повинен допомогти учневі пізнати себе, усвідомити необхідність формування справжньої особистості. Тобто, створювати ситуації, які мають на меті визначення школярем значимої для нього проблеми та пошук шляхів її вирішення. Учитель, щоб організувати творчу діяльність старшокласників, створює або використовує навчальну ситуацію, яка виникає. Її мета – викликати мотивацію і забезпечити діяльність учнів у напрямку пізнання обраної теми й вирішення пов’язаних з нею проблем. Роль вчителя – організаційно-супровідна, оскільки він забезпечує особистісне вирішення учнем створюваного навчального утруднення.

Другою педагогічною умовою є застосування інформаційно-комунікативних технологій на уроках фізики й математики

Формування математичних й фізичних здібностей старшокласників може бути забезпечене систематичним, системним, неперервним навчанням з відповідною спрямованістю методів і форм. Таке навчання сприяє розвитку самостійного засвоєння нового досвіду, нового знання, нових способів і дій.

У контексті нашого дослідження цілеспрямоване застосування методів і форм навчання покликане розвивати у старшокласників компетентність, цілеспрямовану творчість, адаптаційну гнучкість. Нові здатності, що формуються за такої організації навчального процесу, надалі можуть перетворитися у конкретну професійну діяльність з високим рівнем самостійності та усвідомленності.

Формування фізико-математичної компетентності старшокласників потребує визначення відповідних методів і форм, що сприяли б досягненню поставленої мети. У цьому контексті вважаємо слушною думку дослідників-педагогів, які звертають увагу на необхідність спрямування процесу навчання на формування у старшокласників вмінь і навичок самостійно шукати і знаходити необхідну інформацію, а не лише використовувати інноваційні педагогічні технології, що ґрунтуються на активних і емоційно забарвлених формах і методах підготовки [147, с.175].

Однією з важливих складових досягнення цієї мети є впровадження інформаційно-комунікаційних технологій (ІКТ) у навчальний процес. На думку С.А. Ракова: «ІКТ в інформаційному суспільстві, тим більше в суспільстві знань, це значно більше, ніж технологія – це інфраструктура суспільства знань, це важлива складова методології, технології, методики навчальних та наукових досліджень, процесів конструювання…» [178, с. 35].

У педагогічних дослідженнях проблеми використання ІКТ в школах на базі комп'ютерної техніки розробляється у наступних напрямках:

· в загальнотеоретичному та дидактичному (Б. Гершунський,

В. Кузьменко, С. Кузнецов, В. Лисенко, Є. Машбиць,
В. Монахов, В. Роберт, А. Єршов та ін);

· у психолого-педагогічному (Є. Машбиць, Н. Тализіна,
О. Тихомиров, А. Савельєва та ін);

· у розробці, створенні та застосуванні педагогічних програмних засобів (С. Григор 'єв, В. Гріншкун, Є. Бідайбеков, С. Карієв,
Г. Нургалієва, А. Шаріпбаєв та ін.);

· у формуванні математичних компетентностей ( Н. Апатова,
А. Єршов, М. Жалдак, В. Монахов, Н. Морзе, Т. Олійник, С. Раков,
Ю. Рамський , О. Співаковський та ін);

Аналіз педагогічних досліджень показує, що існує безліч ідей і достатній досвід використання програмних засобів навчального призначення в процесі навчання.

Використання сучасних інформаційних технологій в освіті сприяє розкриттю, збереженню і розвитку індивідуальних здібностей учнівської молоді; формуванню пізнавальних інтересів молодих людей, прагненню до самовдосконалення та самореалізації; забезпеченню комплексності вивчення явищ дійсності, нерозривності взаємозв’язку між природознавством, технікою, гуманітарними науками і мистецтвом; постійному динамічному оновленню змісту, засобів, форм і методів навчання і виховання [227].

Саме інформаційно-комунікаційні технології є засобом забезпечення якісних змін у формах і методах навчання, істотного розширення обсягу і характеру доступних людині відомостей, засобів їх одержання і опрацювання. Нерідко можливість аудіовізуального подання різноманітних повідомлень, передусім у поєднанні з кольором і рухом, має значні переваги перед текстовим, графічним чи іншим традиційним повідомленням. Вплив таких повідомлень на людину набагато ефективніший, вони якісно інакше сприймаються і запам’ятовуються, активізують емоційний потенціал особистості, на їх основі утворюються складні асоціативні зв’язки з іншими носіями повідомлень. Саме цим шляхом еволюціонує духовний потенціал людини.

Проведена в системі освіти України значна робота з інформатизації навчальної діяльності у середніх та вищих навчальних закладах дала свої наслідки: розроблено і затверджено Концепцію інформатизації освіти; в усіх регіонах України створено мережу центрів інформатизації та центрів ІКТ; збільшується чисельність навчальних закладів, що оснащені сучасною комп'ютерною технікою, інтегрованою в телекомунікаційні мережі, включаючи глобальну мережу Internet; відбувається послідовна систематизації інформаційних ресурсів вищої школи, оптимізація доступу до них через мережу Internet; накопичено практичний досвід запровадження у середніх навчальних закладах інформаційних технологій навчального призначення різного рівня – від автоматизованих систем управління, інформаційно-аналітичних систем керування діяльністю навчальних закладів до багатофункціональних комплексів і освітньо-наукових порталів; деякі навчальні заклади розвивають технології дистанційного навчання; продовжується формування системи сертифікації програмних педагогічних засобів та інших інформаційних продуктів навчального призначення.

Використання обчислювальної техніки дозволяє опрацьовувати якнайшвидше значні обсяги інформації, враховувати велику кількість чинників, що впливають на стан і розвиток суспільства.

При розробці питання використання ІКТдля формування математичних й фізичних компетентностей ми спиралися на праці, присвячені відбору й конструюванню педагогічних програмних засобів та створенню дидактичних засобів на основі ІКТ (Н. Апатової [8], А. Єршова [68, 69], М. Жалдака [75-79], В. Монахова [148], Н. Морзе [150], Т. Олійник [162], С. Ракова [178-181], Ю. Рамського [182], О. Співаковського [217-219]).

Інформаційно-комунікаційні технології дозволяють будувати процес навчання таким чином, що в зміст навчання включається вивчення стратегій розв’язування задач, у тому числі творчих; забезпечується аналіз і засвоєння учнем своєї власної діяльності. Використання сучасних інформаційно-комунікативних технологій у навчанні призводить до суттєвих змін у методах і організаційних формах навчання, адже воно дозволяє забезпечити включення учня в процес міркування, що моделюється за допомогою комп’ютера, завдяки чому процес засвоєння нових знань здійснюється в умовах опосередкованого комп’ютером спілкування. Постійне стикання в комп’ютеризованих програмних засобах з варіативністю «діалогу» привчає учнів пристосовуватись до необхідності вибору однієї з кількох альтернатив, попередньо спрогнозувавши та оцінивши її доцільність, що сприяє набуттю ними певних як математичних, так і життєвих компетентностей. Використання ІКТ дає можливість ефективного застосування різного типу знань, відкриваючи учневі шляхи до користування будь-яким довідниковим та ілюстративним матеріалом (коментарі й пояснення, цитати й довідки, самі тексти і вказівки, у який спосіб можна їх одержати тощо).

В епоху інформаційного суспільства суттєвого значення набуває проблема ущільненого компонування знань та їх оперативне використання. Тому засвоєння інтегрованих знань, вмінь, здійснене за допомогою нових інформаційних технологій, має низку переваг, а саме: «ущільнює», організовує інформацію, дає змогу виробити індивідуальну траєкторію руху та темп професійної підготовки, відкриває ширші можливості одержання, переробки та використання навчальної інформації, чим поліпшує рівень підготовки учня, піднімає його на якісно новий щабель організації самостійного навчання.

Інформатизація навчання надає широкий спектр засобів для підтримки розвитку особистості кожного учня. Сучасні інформаційні технології створюють сприятливі умови для формування як предметних, так і ключових компетентностей учнів. Цьому сприяє також те, що розв’язування будь-якої задачі із застосуванням комп’ютерних засобів передбачає роботу з різними формами інформації – текстової, цифрової, звукової, графічної – та дозволяє оформлювати результати діяльності за допомогою різноманітних засобів вираження: графіків, звуків, відеозображень тощо.

Для набуття учнями предметних компетентностей при використанні комп’ютера велике значення має зміст завдання. Важливою умовою набуття учнями предметних компетентностей є самостійна, творча робота учнів, про це зазначалося в пункті 2.1. Тому завдання повинно давати поле для самостійного пошуку, творчої діяльності учнів.

Сьогодні існує досить багато навчальних середовищ, які надають учням можливість самостійно проводити експеримент, спостерігати та аналізувати його наслідки, створювати проблемні ситуації та досліджувати їх. У шкільній практиці навчання математики набули поширення програми, які дозволяють проводити такі дослідження. Це програмні засоби «GRAND1», «GRAND2», «GRAND3», «DERIVE», «МathСАD», «МАРLЕ», «MATHEMATICA», «DG», «SchoolGraph», «TepM» та інші, які дозволяють проводити математичні дослідження, побудови на площині й у просторі, знаходити закономірності в математичних явищах, формулювати теореми чи властивості для наступного доведення. Наприклад, педагогічний програмний засіб «GRAND1» дозволяє здійснювати графічний аналіз функцій, надає учням можливість досліджувати властивості тих функцій, які необхідно розглянути при розв’язуванні алгебраїчних завдань; програма «DERIVE» дозволяє знаходити розв’язки рівнянь в числових і буквених виразах, границі функцій, виконувати операції над векторами, робити графічні побудови у двовимірному та тривимірному просторах і ін.; програма «DG» дозволяє будувати динамічні креслення, складати та аналізувати алгоритми побудови цих креслень, ілюструвати задачі й теореми курсу планіметрії; програма «SchoolGraph» (шкільний графобудівник) дозволяє здійснювати графічний аналіз функцій на площині, знаходити значення функції в певній точці.

Застосування інформаційних технологій, окрім допомоги у розв'язанні прикладних питань, має і самостійне значення – розвиває певні особистісні якості, вимагає специфічних знань, умінь, навичок, компетенцій [75]. Слід зазначити, що програмні математичні пакети нині використовуються в різних галузях науки – фізиці, біології, соціології, економіці та ін., тобто мова йде про їхню універсальність, а отже і можливість застосування для розв'язання завдань, обробки інформації міждисциплінарного характеру.

З-поміж них Mathcad справедливо називають не просто математичним, а універсальним математичним пакетом. Згадані пакети програм дають можливість розглянути значну кількість прикладів застосування математики у різних галузях науки та практики, тобто виконують функцію її професійного спрямування, як вияв інтеграції з професійно зорієнтованими дисциплінами.

Необхідно констатувати, що останнім часом процес використання комп’ютерної техніки та інформаційних технологій у навчальних закладах, зокрема при вивченні фізико-математичних дисциплін, дещо активізувався. Це відбулося завдяки покращенню комп’ютерної бази навчальних закладів, наявності на ринку програмного забезпечення потужних проблемно-орієнтованих і спеціалізованих професійних пакетів, зокрема систем комп’ютерної математики Derive, Maple V, Matlab, Мathcad, Mathematica, Maxima, MuPad, пакетів для статистичного аналізу даних Statistica, SPSS, Origin тощо. В цих системах реалізовано багато стандартних і спеціальних операцій і функцій. Все це надає широкі можливості для ефективної роботи старшокласників різних профілей.

Такі пакети треба розглядати як потужний інструмент для підтримки діяльності викладачів, студентів, інженерів, науковців, але ефективність і методична цінність їх як інструменту навчання цілком залежить від майстерності застосування.

Значні перспективи розвитку освітньої галузі відкриває використання мережі Internet, що уможливлює доступ до найновіших інформаційних ресурсів, ознайомлення з наслідками сучасних наукових досліджень, встановлення різнопланових комунікативних зв’язків між всіма учасниками навчального процесу, забезпечує підґрунтя для впровадження нової форми навчання – дистанційної. Можливість інтенсивного спілкування між тим, хто навчається, і тим, хто навчає, підсилення діяльнісної основи, індивідуалізація навчання виводить цю форму на якісно новий рівень у системі освіти в цілому.

Використання комп’ютера в навчальному процесі спрямоване, передусім, на розв’язування таких чотирьох типів дидактичних завдань.

1. Комп’ютер використовується як допоміжний засіб для більш ефективного розв’язування інших дидактичних завдань. При цьому комп’ютерна навчальна програма надає довідкову інформацію, інструкції, демонстрації, виконує обчислювальні операції.

Комп’ютер дозволяє використовувати дидактичні можливості відео- тааудіоінформації. Технології мультимедіа розширюють можливість пошуку й отримання різноманітної інформації. Значні можливості в організації навчального процесу відкрилися з впровадженням гіпертекстових технологій, які значно розширили та спростили роботу з довідковою інформацією, надали можливість створювати електронні довідники, книги, енциклопедії.

2. Комп’ютер може і повинен використовуватися як допоміжний засіб при засвоюванні складних абстрактних теоретичних понять. Учитель при поясненні використовує комп’ютерну модель поняття, що вивчається. Разом з тим, реалізу-ються нові стратегії навчання. Прикладом цього напрямку розробок є так звані «комп’ютерні навчальні середовища», або «мікросвіти», що є моделями галузей знань, які вивчаються. При засвоюванні певного абстрактного поняття людина спочатку створює його модель, використовуючи як об’єкт для цієї моделі предме-ти, що оточують її, та вивчає внутрішні ознаки і зв’язки цього поняття на моделі.

Найважливіша перевага використання комп’ютера як засобу, що допомагає засвоювати складні абстрактні теоретичні поняття, ґрунтується на сучасному розумінні принципу наочності й полягає в тому, що за умов використання педагогічних програмних засобів типу діяльнісних середовищ учні не тільки спог-лядають явища, моделі явищ, які є об’єктами вивчення, а й здійснюють перетворюючу діяльність з цими об’єктами, вони не є пасивними спостерігачами досліджуваних процесів і явищ, оскільки активно впливають на їх перебіг, при цьому навчально-пізнавальна діяльність набуває дослідницького, творчого характеру.

3. Застосування комп’ютера дозволяє ставити й розв’язувати нові дидактичні завдання, які не розв’язуються традиційним шляхом. Характерними є імітаційно-моделювальні програми (наприклад, комп’ютерні програми з імітації експерименту). У цих програмах об’єктом засвоєння виступають: а) зовнішні параметри того або іншого процесу; б) закономірності, які не доступні для спостереження в природних умовах; в) зв’язки імітованих явищ з тими параметрами, які автоматично задані програмою; г) пошук параметрів, які оптимізують проходження імітованого процесу тощо.

Наприклад, у процесі вивчення математики можна використовувати інстру-ментальні програмні засоби, що дозволяють створювати різні математичні моделі, керувати ними й досліджувати їхню «поведінку» (зокрема, під час вивчення тем, пов’язаних із дослідженням функцій, розв’язуванням рівнянь та нерівностей, розв’язуванням завдань на оптимізацію, моделюванням геометричних об’єктів і ситуацій).

Використання навчального демонстраційного обладнання, з’єднаного з комп’ютером, дозволяє дати учню інструмент дослідження реальних явищ або об’єктів і уникнути негативних наслідків, пов’язаних із зануренням учня у світ символів та імітацій реальних процесів, які подаються на екрані комп’ютера. Стає можливим проведення десятків експериментів за порівняно невеликий відрізок часу при негайному зворотному зв’язку й візуалізації результатів експерименту на екрані. Це дозволяє учню висунути гіпотезу про досліджувану закономірність, підтвердити її або спростувати на підставі спостережуваних результатів.

Таким чином, процес передавання готових знань та їх експериментальна перевірка у традиційній методиці замінюється експериментально-дослідницькою діяльністю учнів, що забезпечує самостійне відкриття учнями закономірностей або властивостей досліджуваних об’єктів, набуття ними математичних компетентностей.

4. Комп’ютер може бути засобом контролю, закріплення при тому, що зміст навчання сповіщається учням традиційними засобами. Наприклад, можна проводити тестовий контроль за допомогою комп’ютера або закріплювати отримані знання та сприяти набуттю учнями компетентностей за допомогою роботи учнів з програмами-тренажерами, наприклад, “Mathtrainer” [155].

Таким чином, реалізуються суттєві дидактичні передумови успіхів у навчанні – емоційне включення, гностичність, наочність навчального матеріалу, дозована мультимодальність навчальних впливів, яка стимулює мимовільну увагу, індивідуалізація темпу подання навчального матеріалу. З використанням ІКТ стає можливим не тільки запропоновувати, показати учням модель об’єкта навчання, а й організувати діяльність учнів щодо її перетворення. Ефективність навчання підвищується тоді, коли учні самостійно будують моделі, а не тільки споглядають їх у готовому вигляді.

Широке використання сучасних педагогічних та інформаційно-комунікаційних технологій у навчальному процесі робить можливим [227, с.239]:

· забезпечення інтенсифікації процесу навчання;

· підвищення навчально-пізнавальної активності учнів;

· забезпечення якості навчання учнів на рівні вимог інформаційного суспільства;

· створення умов для інтелектуального розвитку учнів, розкриття їхнього творчого потенціалу;

· підвищення рівня підготовки випускників та їх конкурентоспроможності на міжнародному ринку інтелектуальної праці;

· підвищення рівня інформаційної культури та інформаційно-комп’ютерної підготовки учнів;

· сприяння формуванню в учнів ключових компетентностей (зокрема компетентностей з ІКТ), а також галузевих і предметних компетентностей, а саме математичних.

Третьою дидактичною умовою євикористання широкого спектру прикладних задач в контексті реалізації компетентнісного підходу..

Державний стандарт базової та повної середньої освіти визначає як основну мету освітньої галузі «Математика» опанування учнями системою математичних знань, навичок і умінь, необхідних у повсякденному житті та майбутній трудовій діяльності, достатніх для успішного оволодіння іншими освітніми галузями знань і забезпечення неперервної освіти; формування в учнів наукового світогляду, уявлень про ідеї та методи математики, про її роль у пізнанні дійсності; інтелектуальний розвиток учнів та ін. Державна цільова соціальна програма підвищення якості шкільної природничо-математичної освіти на період до 2015 року визначає одним із пріоритетів розвитку фізико-математичної освіти необхідність посилення прикладної спрямованості вказаних дисциплін. Важливість її реалізації підкреслено в пояснювальних записках до програм із математики й фізики в усіх класах середньої школи.

Проблема реалізації прикладної спрямованості завжди була і є в полі зору методистів, науковців, авторів підручників. Теоретичне обґрунтування її існування та шляхів розв’язування проведено в роботах О.Александрова, О.Астряба, Г.Бевза, Б.Гнеденка, О.Дубинчук, Ю.Колягіна, В.Пікана, З.Слєпкань, І.Тесленка, В.Фірсова та ін. Зокрема, були сформульовані загальні принципи, які забезпечують шкільному курсу математики прикладну спрямованість (В.Фірсов), розроблені шляхи розв’язування завдань, навчання учнів застосовувати математичні знання на практиці (О.Астряб, Г.Бевз, О.Дубинчук, З.Слєпкань, І.Тесленко), визначені умови реалізації прикладної спрямованості математики в школі (Ю.Колягін, В.Пікан).

Прикладна спрямованість фізико-математичних дисциплін – це орієнтація змісту, методів і форм навчання на застосування законів математики в фізиці, техніці, суміжних науках, професійній діяльності, народному господарстві і побуті. Найефективніша реалізація прикладної спрямованості здійснюється у процесі розв’язування прикладних задач, що виникають поза курсом фізики й математики і розв’язуються математичними методами. Розв’язування задач різних рівнів складності, породжених, як правило, певними виробничими потребами передбачає наповнення змісту курсу прикладними обчислювальними, експериментальними, дослідницькими та якісними задачами.

Задачі відіграють важливу роль у розвитку мислення учнів, проте ефективність формування певних якостей особистості залежить від того, як саме зміст задачі або системи задач відповідає сутності феномена, що формується. Тому вважаємо, що розглядаючи задачний підхід як одну з умов формування предметної компетентності старшокласників, треба добирати задачі прикладного змісту, розв’язування яких активізує мисленнєві процеси, зокрема, сприяє розвиткові логічного й алгоритмічного мислення учнів. Це можливо тоді, коли при вивченні будь-якої теми вчитель звертає увагу на:

· реалізацію міжпредметних зв’язків;

· розширення кругозору шляхом ознайомлення учнів з початками економіки, екології;

· складання і розв’язування задач на місцевому матеріалі;

· складання фізико-математичних моделей прикладних задач при вивченні кожної теми;

· розв’язування задач з елементами дослідження та ін.

У методиці навчання математики існують різні тлумачення поняття «прикладна спрямованість». Ю. Колягін і В. Пікан розрізняють поняття «прикладна» і «практична» спрямованість [108]. На їх погляд «прикладна спрямованість навчання математики – це орієнтація змісту і методів навчання на застосування математики в техніці і суміжних науках; у професійній діяльності; в народному господарстві й побуті». Згідно з таким тлумаченням міжпредметні зв’язки, політехнічна спрямованість охоплюються поняттям «прикладна спрямованість». Прикладна спрямованість сприяє формуванню наукового світогляду і показує роль фізики й математики в сучасному виробництві, економіці, науці. Практична спрямованість навчання вказаних предметів – «це спрямованість змісту і методів навчання на розв’язування задач і вправ, на формування у школярів навичок самостійної діяльності математичного характеру» [108, с.17]. У реальному процесі навчання прикладна і практична спрямованість звичайно функціонують спільно. Дещо інакше розуміємо прикладну спрямованість за В. Даллінгером [58] . Він вважає, що «прикладна спрямованість математичних знань повинна означати як їх практичне застосування, так і теоретичне значення в самій математиці. Лише в цьому випадку буде виховуватися в учнів справжня повага до сили наукових знань». Прикладна спрямованість навчання математики найбільше реалізується під час розв’язування прикладних задач. Під прикладною задачею в «школі здебільшого розуміють задачу, яка виникла поза курсом фізико-математичних дисциплін і розв’язується методами математики й фізики і способами, які вивчаються в шкільному курсі» [216, с. 7].

Прикладні задачі вважаються одним з типів навчальних задач. А до основних етапів розв’язування навчальних задач методисти [216] відносять: 1) аналіз формулювання задачі; 2) пошук плану розв’язування; 3) здійснення плану, перевірку і дослідження знайденого розв’язку; 4) обговорення (аналіз) знайденого способу розв’язування з метою з’ясування його раціональності, можливості розв’язування задачі іншим методом чи способом.

Значну роль прикладних задач у навчанні математики розкрито в працях Л.Соколенко [216], О. Cухорукової [69], В. Швеця [221] та ін. Розглядаючи питання використання прикладних задач, не можна не згадати про дослідження з методики навчання математики (зокрема [174]), у яких висвітлено питання необхідності включення до шкільного курсу математики понять «модель» та «моделювання»; доведено необхідність навчання учнів математичному моделюванню; розроблено загальну методичну схему навчання побудові математичних моделей; зазначено, що відображення в шкільному курсі елементів математичного моделювання сприяє розв’язуванню низки важливих педагогічних завдань: посиленню прикладної спрямованості; формуванню елементів математичної і загальної культури; засвоєнню міжпредметних зв’язків та ін. У цих дослідженнях серед іншого обґрунтовано, що навчати учнів побудові математичних моделей доцільно під час розв’язування прикладних задач.

Побудова математичної моделі є найбільш відповідальним і складним етапом розв’язування прикладної задачі. Реалізація цього етапу вимагає від учнів багатьох умінь: виділяти істотні фактори, що визначають досліджуване явище (процес); вибирати математичний апарат для побудови моделі; з’ясовувати фактори, що викликають похибку під час побудови моделі. Також розв’язування таких задач показує практичне застосування математичного апарату, що вивчається в школі, тим самим пробуджує інтерес в учнів до вивчення предмета. Математика стає «потрібна» учневі. З позитивних моментів також варто відзначити, що, розв’язуючи подібні задачі на уроках математики, природним шляхом здійснюється функція інтеграції шкільних предметів.

Розв’язуючи прикладну задачу, слід навчити учнів застосовувати суттєві ознаки поняття математичної моделі. Ми будемо спиратися на означення, яке дає А. Горстко [47, c . 7-8]. Математична модель – наближений опис якого-небудь явища зовнішнього світу, яке виражене за допомогою математичної символіки і яке замінює вивчення цього явища дослідженням і розв'язанням математичних задач.

Математична модель потрібна, щоб:

· зрозуміти, як улаштований конкретний об’єкт, яка його структура, основні властивості, закони розвитку і взаємодія з навколишнім світом;

· навчитися керувати об’єктом (або процесом) і визначити найкращі способи керування з певною метою і критеріями;

· прогнозувати прямі і непрямі наслідки реалізації заданих способів і форм впливу на об’єкт.

У процесі побудови математичної моделі прикладної задачі звичайно виникає потреба побудови математичних моделей реальних об’єктів, про які йдеться в задачі.Математичні й фізичні моделі реального процесу або об’єкта можуть бути подані у вигляді формули, малюнка, твердження, геометричної фігури, пропорції тощо. У реальному житті є багато задач, які, на перший погляд, не мають між собою нічого спільного. Але часто для їх розв’язування можнавикористовувати одну й ту саму модель. Виходить, що вміння працювати з однією моделлю дає можливість знаходити розв’язання різних прикладних задач. Вважаємо, що процес моделювання можна подати у вигляді схеми на рис. 2.2

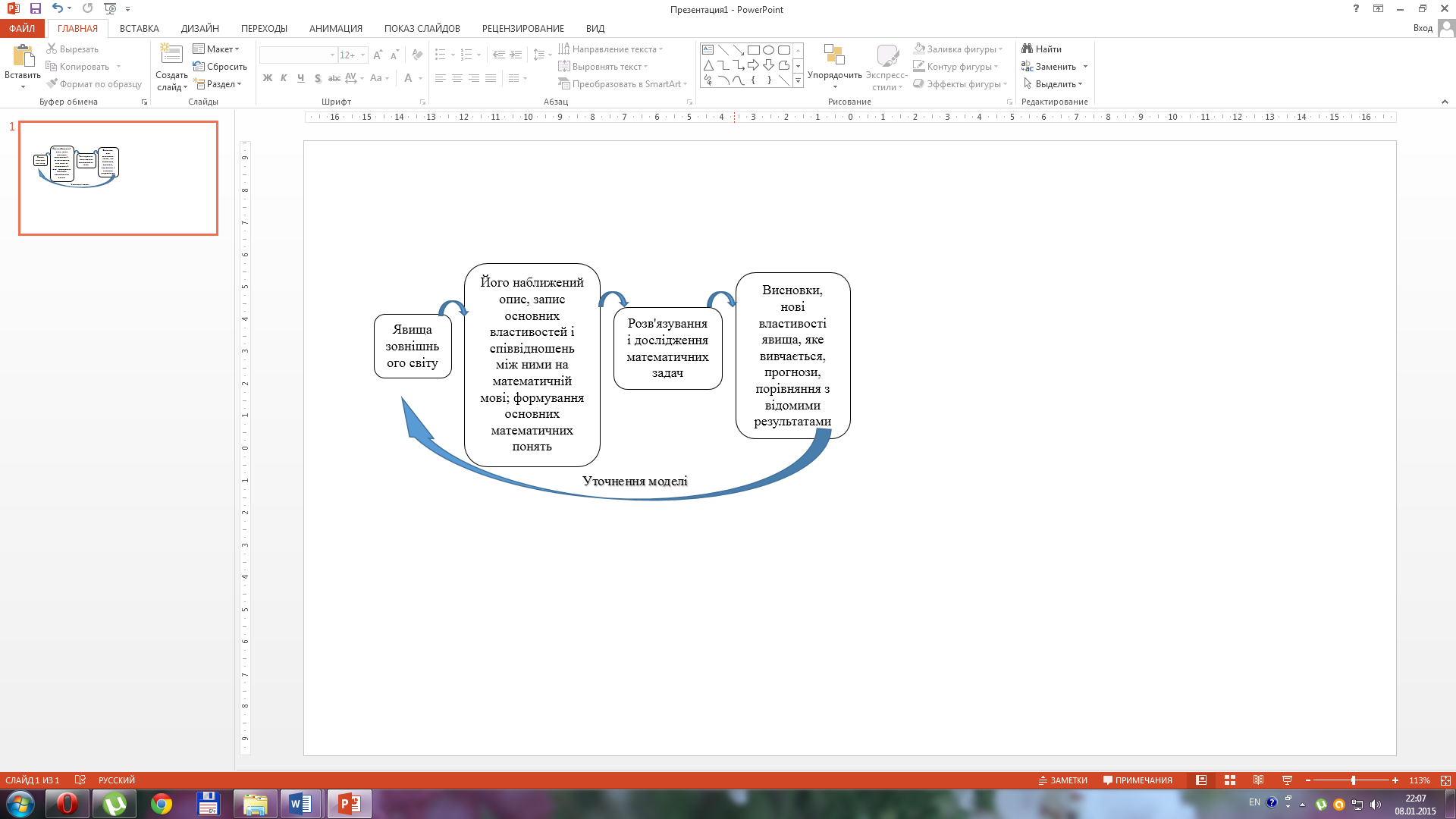
Рис. 2.2Процес моделювання з предметів фізико-математичного циклу

Таким чином, моделі, за допомогою яких дослідження явищ зовнішнього світу зводиться до розв'язання математичних й фізичних задач, займають провідне місце серед інших методів дослідження і дозволяють не тільки пояснити явища, які спостерігають, а і зазирнути туди, де ще в принципі не могло бути дослідних, експериментальних даних. Саме так було при проведенні перших атомних і водневих вибухів. І це ще не все. Існують сфери людської діяльності, де проведення експериментів, одержання експериментальних результатів принципово неможливо.

Як правило, труднощі, пов’язані із засвоєнням знань з фізики й маиематики та способів діяльності з об’єктами, пояснюються тим, що учні не підготовлені до виконання тих розумових дій, які входять до складу основних видів пізнавальної діяльності, пов’язаної з математикою й фізикою.

Для набуття учнями предметних компетентностей при розв’язуванні прикладних задач важливу роль відіграє виділення та засвоєння орієнтовних основ відповідних дій. Так, при розв’язуванні прикладних задач учню треба:

· Створити фізико-математичну модель даної задачі (перекласти умову прикладної задачі на мову математики або фізики). В умові задачі задається деякий «не фізико-математичний» об’єкт. Спочатку виявляються основні особливості, явища і зв’язки між ними на якісному рівні. Потім знайдені залежності формулюються мовою математики, тобто будується математична модель.

· Розв’язати одержану математична або фізичну задачу. На цьому етапі велика увага приділяється розробці алгоритму і методів розв’язування задачі, за допомогою яких результат можна знайти з необхідною точністю і за припустимий час. Тут важливу роль набувають математичний апарат, необхідний для аналізу математичної моделі, і обчислювальна техніка – могутній засіб для одержання кількісної вихідної інформації як результату розв’язування складних математичних задач.

· Проаналізувати відповіді. На цьому етапі з’ясовується, чи відповідають результати експерименту теоретичним наслідкам моделі в межах визначеної точності. Потрібно повернутися до початкової умови, ніби «примірити» розв'язки математичної задачі до змісту прикладної задачі. Іноді в результаті такого «приміряння», або, як говорять, інтерпретації, з’ясовується, що розв'язки математичної задачі або не можуть бути розв’язками прикладної задачі, або виникає потреба в додаткових дослідженнях і перетвореннях, щоб задовольнити умови прикладної задачі. У процесі розвитку науки і техніки дані про досліджувані явища усе більше і більше уточнюються і настає момент, коли висновки, що одержують на основі існуючої математичної моделі, не відповідають нашим знанням про явище. Таким чином виникає необхідність побудови нової, досконалішої математичної моделі. Аналіз знайдених результатів обов’язковий у процесі розв’язування прикладних задач.

Прикладні задачі можна умовно поділити на такі, у яких математична модель міститься в умові задачі, та такі, розв’язання яких передбачає побудову математичної моделі. Розв’язування неформалізованих прикладних задач складається з наступних етапів:

ü постановка задачі;

ü переклад умов задачі на мову математики;

ü складання математичної моделі задачі;

ü пошук плану розв’язування задачі всередині моделі;

ü здійснення плану, перевірка і дослідження знайденого розв’язку в середині моделі;

ü інтерпретація отриманого результату;

ü обговорення (аналіз) знайденого способу розв’язування з метою з’ясування його раціональності, можливості розв’язування задачі іншим методом чи способом.

Задачі з практичним змістом доцільно розв’язувати при вивчені кожної теми. Це сприяє підвищенню інтересу учнів та поетапному формуванню в них практичної компетентності.

Одне з важливих умінь учнів при розв’язанні прикладних задач є перенесення знань, умінь і досвіду в нові умови. Це можливо, якщо вчитель:

- виділяє провідні знання;

- цілеспрямовано працює над освідомленням учнями суттєвих ознак кожного з визначених провідних (базових) понять;

- виховує в учнів гнучкість мислення – здібність швидко і легко переходити від одного класу явищ до іншого, далекого за змістом;

- формує здібності до оцінки (вчить оцінювальні дії проводити не тільки при завершенні роботи, а і по ходу її);

- вчить передбачати результати виконаних дій;

включає до системи завдань задачі з виробничо-технічним змістом, винахідницькі та експериментальні задачі та ін. [196, c . 32-35].

Отже, на підставі вищенаведене можна сказати, для того, щоб сформувати предметну компетентність, вчителю треба при вивченні кожної теми належну увагу приділяти розв’язуванню задач прикладного змісту, які спонукають думати, зіставляти різні методи; сприяють розвитку мислення (творчого, критичного), яке характерне для старшокласників і застосуванню різних способів вираження думки; інтуїції – здатності передбачати результат і знаходити шлях до розв’язання; знаходити їм практичне застосування.

Таким чином, узагальнюючи розглянутий матеріал, процес формування розвитку предметної компетентності школярів старшої школи, можна представити у вигляді схеми, яка зображена на рисунку 2.3. Запропонована схема повністю реалізує склад предметної компетентності до складу якої входить процедурна, логічна, конструктивно-графічна, дослідницька та методологічна компетентності.

До складу наведеної схеми формування предметної компетентності відповідно до логіки нашого дослідження входять чотири блоки: цільовий, концептуальний, змістовно-процесуальний та оцінювальний.

1. Цільовий блок включає у себе мету та завдання розробленої схеми.

2. Концептуальний блок. До складу цього блоку входять наукові підходи, які покладені в основі формування предметної компетентності старшокласників у процесі вивчення фізики й математики, саме компетентнісний, діяльнісний (п.п. 1.1, 1.2, 2.2).

3. Змістовно-процесуальний блок включає в себе дидактичні умови (реалізація яких забезпечить формування предметної компетентності старшокласників), зміст, технології, форми та види діяльності старшокласників під час вивчення фізики й математики (п.п. 1.2, 2.2).

4. Оцінювальний блок, який містить критерії сформованості фізичної компетентності, показники їх вияву, рівні (п.п. 1.3), а також результат, який представляє сформовану предметну компетентність.

Узагальнюючи все вищенаведене можна сказати, що формування предметної компетентності старшокласників у процесі вивчення предметів фізико-математичного циклу представляє собою складний педагогічний процес, який доцільно розглядати з позиці системного підходу. Запропонована методика реалізації дидактичних умов спрямована на підвищення у старшокласників рівня сформованості предметної компетентності у процесі вивчення предметів фізико-математичного циклу.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Та традиційного підходів до організації навчального процесу	\|	Реалізація дидактичних умов формування предметної компетентності в учнів старшої школи

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.037 сек.