
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Реалізація дидактичних умов формування предметної компетентності в учнів старшої школи
Сформованість предметної компетентності старшокласників є кінцевим результатом функціонування запропонованої нами схеми в п.2.3.
Для того щоб досягти бажаного результату, слід визначитися з послідовністю впровадження запропонованих умов, тобто виявити етапи реалізації схеми, які забезпечать сформованість предметної компетентності старшокласників. Розроблену схему дидактичних умов доцільно розглядати з позиці системного підходу. Використання зазначеного підходу дозволило вивчити і розробити методичну систему предметної компетентності.
Вивчення праць учених показує, що методична система розглядається в таких аспектах, як: сукупність компонентів (структурних та функціональних), взаємодія яких обумовлює високий рівень організації процесу навчання (В. Монахов [1]); система, у якій протікають педагогічні процеси (В. Безпалько [2]); модель досліджуваного педагогічного процесу (Г. Сєріков [3]). Але спільним для всіх наведених означень є те, що методична система складається з деякої сукупності елементів, тобто мінімальних структурних одиниць, кожна з яких виконує власну функцію і взаємодіє з іншими елемента. Основною метою створення методичної системи є забезпечення успішного формування предметної компетентності старшокласників.
Формування предметної компетентності учнів старшої школи здійснюється як під час уроків з предметів фізико-математичного циклу, так й у позаурочній діяльності. Як відомо, урок - одне з найскладніших дидактичних явищ. Існує декілька концептуальних підходів до тлумачення сутності уроку, автори яких розглядають цей дидактичний феномен з різних методологічних позицій. Фундаментальні дидактичні праці, присвячені вивченню сутності уроку та урочної форми навчання належать Ю.Бабанському [7], В. Краєвському [8], І. Лернеру [9], М. Махмутову [10], М. Скаткіну [11]]. У межах схеми формування предметної компетентності учнів старшої школи ми не ставимо собі за мету висвітлити сутність цих та інших дидактичних концепцій, лише зазначимо, що стосовно вивчення предметів фізико-математичного циклу урок, за М. Махмутовим, є «формою руху навчання, яка визначається змістом, принципами, методами навчання, планована й регульована у певних просторово-часових межах та здійснювана спільно вчителем й учнем» [10].
Та використання лише урочних форм, навіть і здійснюваних у нетрадиційній формі, для формування предметної компетентності учнів старшої школи недостатньо. Тому ефективною формою навчальної діяльності для формування предметної компетентності старшокласників є спецкурси.
Уроки та спецкурси з предметів фізико-математичного циклу є різновидами методичної системи.
На підставі вищезазначеного побудуємо методичну систему вказаних форм організації навчання старшокласників.
Аналіз наукової літератури [4, 5] дає підстави говорити, що методична система виконує певні функції. На нашу думку, до основних функцій досліджуваної методичної системи необхідно віднести наступні:
- методологічну – спрямовану на формування у школярів системного підходу до вивчення фізико-математичних дисциплін;
- гуманістичну – спрямовану на ствердження у навчально-виховному процесі цінності особистості школяра;
- інтегративну – забезпечує системне засвоєння фізико-математичних наук і формування у школярів цілісної наукової картини світу;
- мотиваційну – спрямовану на формування мотивації школярів до вивчення фізико-математичних дисциплін;
- рефлексивну – забезпечує усвідомлення учнями власної діяльності, у процесі якої здійснюється оцінка своїх здібностей та можливостей.
Будь-яка система має певну структуру, під якою розуміють сукупність стійких зв’язків між об’єктами, які забезпечують її цілісність і тотожність самій собі, тобто збереження основних властивостей при різних зовнішніх і внутрішніх змінах [4]. Структура методичної системи поєднує компоненти уроків фізики й математики та спецкурсів у єдине ціле і надає системі внутрішньої форми і порядку.
При побудові методичної системи вказаних форм організації навчання ми спиралися на роботи В.Монахова[6] і відштовхувалися від того, що:
- методична система включає у себе цільовий, змістовий, технологічний (методи та засоби навчання, форми організації навчальної діяльності) компоненти;
- перебіг будь-якого процесу передбачає поетапність(у процесі уроків та спецкурсів можна виділити наступні етапи: підготовчий, змістовно-організаційний та оцінно-рефлексивний);
- результативність процесу залежить від умов, за яких він перебігає.
Кожна підсистема методичної системи є також системним об’єктом, який виконує певні функції і в їх межах виявляє свою активність і самостійність [5].
Так, цільовий компонент як підсистема уроків та спецкурсів включає навчальні, виховні й розвивальні цілі.
До складу технологічного компоненту входять методи та засоби навчання, форми організації навчальної діяльності старшокласників (п.п. 1.3).
Для реалізації обраних методів навчання можна використовувати індивідуальні, фронтальні, групові та колективні форми організації навчальної діяльності старшокласників, які конкретизовані відносно методів навчання (рис. 2.4).
| Форми організації навчальної діяльності старшокласників |
| Індивідуальні |
| Фронтальні |
| Групові |
| Колективні |
| Диференційо- вані завдання |
| Індивідуальні завдання |
| Індивідуальні проекти |
| Опитування |
| Словесні методи |
| Групова навчально-дослідницька діяльність |
| Групові проекти |
| Колективна навчально-дослідницька діяльність |
| Колективні проекти |
Рис. 2.4. Форми організації навчальної діяльності старшокласників
Як видно зі схеми, до індивідуальних форм організації навчальної діяльності ми віднесли диференційовані та індивідуальні завдання, індивідуальні проекти.
Індивідуальні проекти дозволяють вивчати питання міжпредметного характеру, пов’язуючи фізику й математику з іншими природничими та технологічними науками.
До групових форм організації навчальної діяльності віднесли: групову навчально-дослідницьку діяльність, групові проекти.
До колективних форм організації навчальної діяльності віднесли: колективну навчально-дослідницьку діяльність, колективні проекти.
Для успішного впровадження методичної системи необхідно використовувати систему засобів навчання, до якої входять: а) вербальні (підручники з математики й фізики, дидактичні матеріали, довідники, енциклопедії); б) наочні (таблиці, малюнки, моделі, реальні об’єкти тощо); в) технічні засоби (екранні, звукові, мультимедійні, комп’ютер, проектор, фотоапарат та інше).
Змістовий компонент як підсистема включає наступні елементи:
- знання з математики й фізики, які покладені в основу шкільного курсу і включають основні поняття, терміни, закони, наукові факти і фундаментальні ідеї, основні методи, моделі, теорії фізики й математики;
- способи діяльності втілюються в уміннях та навичках школярів використовувати набуті знання з фізико-математичних дисциплін при пояснені природних явищ у навколишньому середовищі, побуті, техніці, при розв’язуванні завдань різного характеру;
- досвід творчої діяльності проявляється в умінні школярів переносити засвоєні раніше знання у незвичні ситуації, пошуку альтернативних та оригінальних шляхів розв’язання поставлених завдань (при цьому розвивається гнучкість мислення).
В основу методичної системи покладені такі загальнодидактичні принципи (наочності, свідомості і активності, доступності, науковості, індивідуалізації навчання, систематичності та послідовності навчання, забезпечення міцності результатів навчання).
Останнім етапом у побудові методичної системи є виділення дидактичних умов:
· створення позитивної мотивації у старшокласників до навчально-пізнавальної діяльності, спрямованої на формування предметної компетентності у процесі вивчення фізики й математики;
· використання широкого спектру прикладних задач в контексті реалізації компетентнісного підходу;
· застосування інформаційно-комунікативних технологій на уроках фізико-математичного циклу.
Вказані умови були розглянуті нами у п.2.3.
Таким чином, нами побудована методична система реалізації дидактичних умов для успішного формування предметної компетентності старшокласників у процесі вивчення предметів фізико-математичного циклу.
Методична система уроків та спецкурса з предметів фізико-математичного циклу складається з шести структурних елементів: мети, методів, засобів, змісту навчання, форм організації навчальної діяльності, результативного компоненту.
Для того щоб досягти бажаного результату, слід визначитися з послідовністю впровадження запропонованих дидактичних умов, тобто виявити етапи реалізації схеми, які забезпечать підвищення рівня сформованості предметної компетентності старшокласників в процесі вивчення предметів фізико-математичного циклу.
Упровадження схеми відбувалося поетапно.
Метою створення позитивної мотивації у старшокласників до навчально-пізнавальної діяльності є усвідомлення значущості і цінності фізики й математики в сучасному суспільстві, необхідності фізико-математичної підготовки у професійному контексті.
Наявність в учнів позитивної навчальної мотивації є основою ефективності навчального процесу.
Вихованню позитивної мотивації навчання сприяють загальна атмосфера у школі, класі; участь учня в колективних формах організації різних видів діяльності; відносини співпраці вчителя й учня, допомога вчителя не у вигляді прямого втручання у виконання завдання, а у вигляді порад, залучення вчителем школярів до оціночної діяльності і формування в них адекватної самооцінки.
Формування мотивації визначається її резервами в кожному віці, як зазначає В.Давидов зоною її «найближчого розвитку»[12]. Ці резерви не актуалізуються самі по собі, а мобілізуються тільки в процесі активного включення школярів у навчальну діяльність.Організувати таку розвивальну діяльність має вчитель.
Залежно від змісту уроку вчитель повинен організовувати певний цикл навчальної діяльності і формувати відповідний їй мотиваційний цикл. Мотивація навчання на уроці відбувається в кілька етапів:
І — мотивація початку роботи, первинна мотивація.
ІІ — мотивація виконання роботи, закріплення і підсилення первинної мотивації.
ІІІ — мотивація завершення уроку (результативність, постановка цілей на майбутнє) [13].
Завдання вчителя полягає у забезпеченні постійних мотиваційних дій учня на всіх етапах уроку. За змістом мотивація може бути різною.
Розглянемо методичні рекомендації до виконання кожного із етапів мотивації на уроці.
Етап первинної мотивації. На початку уроку учень повинен зрозуміти, що корисного і нового він дізнається у ході роботи, де може застосовувати набуті знання. Учитель може використати кілька видів спонукання учнів до навчальної діяльності:
- активізувати мотиви, що виникли на попередніх заняттях: «Ми добре попрацювали над попередньою темою... Вивчили... Навчилися...»;
- збудити мотиви незадоволеності своїми результатами: «Але не до кінця розібралися з такими важливими питаннями теми...»;
- посилити мотиви орієнтації на попередню діяльність: «На майбутнє це вам знадобиться вжитті в таких-то ситуаціях. Без цього неможливо буде добре зрозуміти нашу наступну тему...».;
- посилити мотиви здивування, зацікавленості.
Наведемо приклад етапу первинної мотивації, яка відбувається на уроці алгебри 10 класу з теми «Показникові рівняння».
ТЕМА: Показникові рівняння
МЕТА УРОКУ: керувати діяльністю учнів по формуванню поняття про показникові рівняння, способи розв’язування цих рівнянь, розвивати логічне мислення, математичне мовлення учнів.
ТИП УРОКУ: постановка та розв’язування навчальної задачі.
ПЛАН УРОКУ:
| № п.п. | Завдання | Мета завдання | Форми організац.,методи | Час |
| 2. | Корекція знань.
1) Завдання на дошці:
а) у=3х+х2; у=3х; у=log2x;
у=  +3.
Питання вчителя:
назвати показникові функції, довести свій вибір, побудувати графіки показникових функцій, дослідити їх. +3.
Питання вчителя:
назвати показникові функції, довести свій вибір, побудувати графіки показникових функцій, дослідити їх.
| Вид спонукання: активізувати мотиви, що виникли на попередніх заняттях; - систематизувати знання учнів з поняття показникова функція, властивості показникової функції; - Створити ситуацію «успіху» - здійснювати рефлексію учнівських дій. | Фронтальна робота. Метод контролю, самоконтролю. | 7 хв. |
2)Розв’язати рівняння:
а)4х+lgх=10+lgх;
б)Х2+2х+5=10х;
в)Х4=12; 8х=2;
г)  =3.
Учні мають проблеми із розв’язуванням в), г) рівняннями
Далі накопичувати незнання про показникові рівняння, показати, що це не одиничний випадок, а новий вид рівнянь, які пов’язані з показниковою функцією. =3.
Учні мають проблеми із розв’язуванням в), г) рівняннями
Далі накопичувати незнання про показникові рівняння, показати, що це не одиничний випадок, а новий вид рівнянь, які пов’язані з показниковою функцією.
| Вид спонукання : збудити мотиви незадоволеності своїми результатами. Створити проблемну ситуацію; - здійснювати рефлексію учнівських дій. | Індивідуальна робота, проблемно-пошуковий: «мозковий штурм» |
Етап закріплення і посилення мотивації. На цьому етапі вчитель орієнтується на широкий спектр пізнавальних і соціальних мотивів навчання. Можуть бути використані чергування різних видів діяльності: репродуктивних і пошукових, усних і письмових, індивідуальних і фронтальних. Крім того, формуванню мотивації сприяє зацікавленість учнів методом викладу матеріалу:
- цікаві приклади, досліди, парадоксальні факти, історичні екскурсії;
- незвична форма подання матеріалу, що викликає здивованість в учнів;
- емоційність мови вчителя;
- пізнавальні ігри;
- дискусії;
- аналіз життєвих ситуацій;
- вміле застосування вчителем заохочення.
Особливого значення при цьому набуває вміння учня вчитися. Це передбачає, що учень має:
- зрозуміти, що таке знання;
- досягнути поставлених цілей у роботі та суспільно корисній діяльності;
- знати, як людина оволодіває знаннями і що засвоєння знань забезпечуються увагою, сприйняттям, усвідомленням, узагальненням і запам'ятовуванням;
- знати, як людина оволодіває знаннями і що засвоєння знань забезпечуються увагою, сприйняттям, усвідомленням, узагальненням і запам'ятовуванням;
- привчати себе до постійного повторення вивченого матеріалу, прагнути дізнаватися більше.
Особливу увагу вчитель має приділяти шкільній оцінці, підключати учнів до самоконтролю і самооцінки. На формування позитивної мотивації впливає спосіб ознайомлення учнів з оцінкою. Наприклад, учитель не тільки констатує факт, а обов'язково хвалить учня за кожне нове досягнення у засвоєнні навчального матеріалу.
Етап завершення уроку. На цьому етапі важливим є вихід учня із діяльності з позитивним власним досвідом і виникнення позитивної установки на навчання у майбутньому, тобто позитивної мотивації перспективи. Для формування такої мотивації не завжди доцільно вести мову про успіхи учнів. Важливо також показати учням їх слабкі місця, щоб сформувати в них об'єктивне уявлення про свої можливості. Це зробить їх перспективну мотивацію дієвішою.
Таким чином, кожен етап уроку повинен бути вмотивований, учням необхідно показувати значущість теми уроку, завдання, які школярі виконують на уроці при цьому вчителю необхідно наповнити психологічним змістом кожен етап уроку, бо «кожен етап — це специфічна за своїм мотиваційним змістом психологічна ситуація»[12].
Одним із завдань, які посилюють позитивну мотивацію навчальної діяльності учнів, є використання широкого спектру прикладних задач (п.п. 2.2.).
Метою використання широкого спектру прикладних задач на уроках математики й фізики для учнів 10-11 класів є удосконалення компетентності для здійснення особистісного професійного розвитку щодо формування в учнів практичних навичок застосування знань фізико-математичних дисциплін, усвідомлення значущості і цінності фізики й математики в сучасному суспільстві.
Прикладні задачі – найскладніший тип задач в математиці й фізиці.
Ці задачі є одним з типів навчальних задач. До основних етапів розв’язування навчальних задач відносять: 1) аналіз формулювання задачі; 2) пошук плану розв’язування; 3) здійснення плану, перевірку й дослідження знайденого розв’язку; 4) обговорення (аналіз) знайденого способу розв’язування з метою виділення загального плану розв’язування для задач даного типу, можливості розв’язування задачі іншим методом чи способом.
Як правило, труднощі, пов’язані із розв’язуванням прикладних задач, пояснюються тим, що учні не підготовлені до виконання тих розумових дій, які входять до складу основних видів пізнавальної діяльності, пов’язаної з фізико-математичними дисциплінами. Тому адекватні кожному виду діяльності розумові дії повинні стати не тільки засобом, а й предметом засвоєння учнів [14]. Для набуття учнями предметних компетентностей при вивченні математики й фізики важливу роль відіграє виділення та засвоєння орієнтовних основ відповідних дій при розв’язуванні задач. При цьому швидкість набуття старшокласниками відповідних компетентностей (перш за все процедурної) безпосередньо залежить від ступеня загальності та дієвості тих орієнтирів, які входять до орієнтовних основ.
Для організації поетапного формування розумових дій при розв’язуванні прикладних задач нами підібрано систему різнорівневих задач для ознайомлення учнів з основними методами і прийомами їх розв’язування з метою набуття ними процедурної компетентності.
Ознайомлення учнів з основними методами і прийомами розв’язування прикладних задач на будь-якому рівні навчання доцільно провести вже на початку 10 класу під час уроків систематизації та узагальнення матеріалу основної школи у вигляді бесіди за таким планом:
1. Мотивація необхідності узагальнення методів розв’язування прикладних задач.
2. Виділення для учнів орієнтовної основи діяльності з розв’язування задач за допомогою складання фізико-математичних моделей.
Після бесіди доцільно організувати у формі фронтальної роботи поелементне коментоване виконання учнями розв’язування задач за допомогою фізико-математичних моделей та рівносильних перетворень з використанням виділених орієнтовних основ (етап зовнішньої мови). На наступному уроці організується диференційована самостійна діяльність учнів з розв’язування прикладних задач за виділення фізико-математичної моделі та рівносильних перетворень (етап внутрішньої мови). Диференціація здійснюється як за рахунок рівня складності завдання, так і за рахунок варіювання міри допомоги різним групам учнів [14].
Коротко охарактеризуємо вище зазначені етапи роботи.
1. Ураховуючи, що основним внутрішнім мотивом навчальної діяльності для більшості учнів 10 класу є орієнтація на результат(п.п. 2.1, 2.2),головним аспектом мотивації може бути пояснення вчителя, що в основній школі прикладні задачізастосовувалися рідко, алгоритм розв’язування таких задач вимагав знання однієї конкретної теми, але вже в 10 класі вони будуть розглядати прикладні задачі, для розв’язування яких не вдається запропонувати алгоритми і тому для їх розв’язування дуже важливим є володіння загальними методами розв’язування прикладних задач, що дозволить розв’язувати різноманітні задачі вказаного типу в 10 – 11 класах на випускних іспитах та під час зовнішнього незалежного оцінювання з математики й фізики. Крім того, учитель наголошує, що вміння розв’язувати прикладні задачі допоможе розв’язувати цілу низку задач з економіки, хімії, біології та інших дисциплін.
2. Організувати виділення орієнтовних основ діяльності з розв’язування прикладних задач за допомогою виділення фізико-математичної моделі, а саме:
- формалізація, переклад запропонованої задачі на математичну чи фізичну мову. Зведення (шляхом перетворення або переформулювання) задачі з прикладним змістом до іншої, їй еквівалентної, але уже стандартної задачі (математичної чи фізичної);
– рішення стандартної задачі;
– інтерпретація отриманого рішення. Переклад отриманого результату (математичного чи фізичного рішення) на мову, на котрій була сформульована початкова задача.
У процесі розв’язування прикладних задач здійснюється навчання учнів елементам математичного моделювання, адже найбільш відповідальним і складним етапом розв’язування прикладної задачі є побудова її математичної моделі. Реалізація цього етапу вимагає від учнів багатьох умінь: виділяти істотні фактори, що визначають досліджуване явище (процес); вибирати математичний апарат для побудови моделі; виділяти фактори, що викликають похибку при побудові моделі. Детальніше побудову моделі ми розглядали в п.п.2.2.
Ці орієнтовні дії представимо у вигляді схеми
| ММЗ |
| РМЗ |
| РПЗ |
| ПЗ |
Рис. 2.6. Орієнтовна схема розв’язування прикладної задачі.
Виділення орієнтовної основи дій при розв’язуванні прикладних задач розглянемо на конкретному прикладі.
Приклад. Як загородити земельну ділянку прямокутної форми проволокою довжина якої а метрів, причому одна сторона ділянки прилягає до будівлі так, щоб площа огорожі була найбільшою.
Розв’язання.
1. Переведемо задачу на математичну умову (складемо математичну модель).
Треба знайти найбільше значення функції у=S(x) на проміжку [0; 
 ].
].
S(x)=x(a-2x), де х - довжина однієї сторони огорожі.
2. Розв’яжемо математичну задачу.
S”(x)=(ax-2x2)”=-4<0, тому Smax=0,125a2(м2), друга сторона ділянки дорівнює 0,5а (м).
3. Відповідь: сторони огорожі 0,5а, 0,25а.
Розглянемо прикладні задачі, що розв’язуються за допомогою тригонометричних, ірраціональних, показникових та логарифмічних рівнянь. Прикладні задачі, пов’язані з розв’язуванням рівнянь та нерівностей, відсутні (чи майже відсутні) у більшості підручників для старшої школи.
Дидактичні цілі, що досягаються в процесі розв’язування прикладних задач під час вивчення рівнянь і нерівностей у курсі алгебри та початків аналізу, – це:
1) підготовка до вивчення учнями тригонометричних, ірраціональних, показникових та логарифмічних рівнянь і нерівностей, зокрема, шляхом сприяння концентрації уваги учнів на новому виді рівнянь та нерівностей; забезпечення мотивації навчання; створення проблемної ситуації;
2) закріплення набутих теоретичних знань та формування в учнів відповідних математичних компетентностей;
3) розвиток логічного мислення учнів завдяки використанню аналітико-синтетичних розмірковувань у процесі розв’язування;
4) контроль набуття учнями предметної компетентності з розв’язування рівнянь та нерівностей.
У залежності від дидактичних цілей, що ставляться вчителем, прикладні задачі можна використовувати на різних етапах уроку, наприклад, при введенні нових понять, а також у самостійній роботі учнів.
Розглянемо прикладні задачі, математичними моделями яких є тригонометричні рівняння. Так, при введенні поняття тригонометричного рівняння доцільно розв’язати з учнями наступну задачу.
Задача 1. Куля масою m, що висить на нитці, здійснює коливання. Коли куля перебуває в положенні рівноваги, сила натягунитки дорівнює  На який максимальний кут
На який максимальний кут 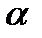 від вертикального положення відхиляється куля?
від вертикального положення відхиляється куля?
Розв’язання.
Швидкість кулі в нижній точці можна знайти із другого закону Ньютона:  Згідно із законом збереження енергії
Згідно із законом збереження енергії  де, як бачимо на рисунку 2.2,
де, як бачимо на рисунку 2.2,  Звідси
Звідси 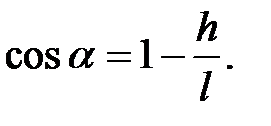
Аналіз даної задачі приводить до висновку, що існують рівняння, у яких невідоме є аргументом тригонометричної функції, і саме такі рівняння називають тригонометричними.
| h |
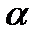
|
| l |
Рис. 2.7. Рисунок до задачі 1
Усвідомленню учнями ролі тригонометричних рівнянь як математичних моделей певних реальних явищ і процесів сприятиме розв’язання наступної задачі.
Задача 2. По прямому шосе рухається автобус зі швидкістю 16 м/c. Попереду руху автобуса в полі, на відстані 60 м від шосе та 400 м від автобуса, перебуває людина, яка може бігти зі швидкістю 4 м/c. У якому напрямі вона повинна бігти, щоб встигнути “перехопити” автобус?
Розв’язання. Нехай автобус знаходиться в точці А, а людина в точці В
(рис. 2.8). Знайдемо, під яким кутом  до лінії АВ повинна бігти людина, щоб опинитися на шосе в деякій точці С до того, як там опиниться автобус або одночасно з ним. Час руху автобуса
до лінії АВ повинна бігти людина, щоб опинитися на шосе в деякій точці С до того, як там опиниться автобус або одночасно з ним. Час руху автобуса  час руху людини
час руху людини  Звідси маємо:
Звідси маємо: 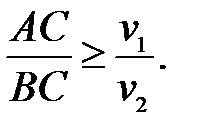 Використавши теорему синусів до трикутника АВС та врахувавши, що
Використавши теорему синусів до трикутника АВС та врахувавши, що  де d – відстань людини від шосе, а s – відстань людини від автобуса, маємо:
де d – відстань людини від шосе, а s – відстань людини від автобуса, маємо: 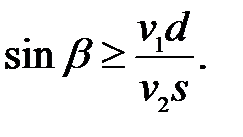 Звідси отримуємо:
Звідси отримуємо: 
Задача 3. Куля, що висить на ниточці, здійснює гармонійні коливання. Визначити період гармонійного коливання цієї кулі, якщо амплітуда коливань  час від початку руху – 1 с, а початкове значення
час від початку руху – 1 с, а початкове значення 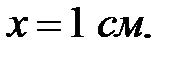
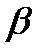
|
| В |

|

|

|
| S |
| d |
| С |
| А |
Рис.2.8. Рисунок до задачі 2
Розв’язання. Учитель нагадує відоме учням з курсу фізики рівняння гармонійних коливань  де t – час від початку руху, w – частота руху
де t – час від початку руху, w – частота руху  Отже, щоб знайти період гармонійного коливання (T), треба знайти частоту руху. Позначимо її через y та отримаємо математичну модель даної задачі:
Отже, щоб знайти період гармонійного коливання (T), треба знайти частоту руху. Позначимо її через y та отримаємо математичну модель даної задачі: 
 Звідки
Звідки 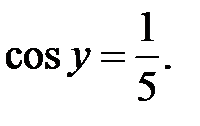 Отже,
Отже,  Звідки
Звідки 
Усвідомленню учнями ролі ірраціональних рівнянь як математичних моделей певних реальних явищ і процесів сприятиме розв’язання наступної задачі.
Задача 4. Повний опір електричного ланцюга, який складається із резистора, конденсатора ємністю С = 0,1 мкФ та котушки індуктивністю L = 0,5 Гн, складає 1800 Ом. Він підключений до мережі з частотою v = 1000 Гц. Знайти опір резистора.
Розв’язання. Вчитель нагадує відому учням із курсу фізики формулу розрахунку повного опору (Z):  , де R – опір резистора,
, де R – опір резистора, 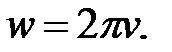 Отже, якщо підставити відомі значення, то отримаємо рівняння:
Отже, якщо підставити відомі значення, то отримаємо рівняння: 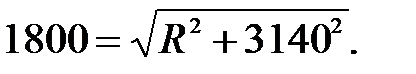 Піднісши ліву та праву частину останньої рівності до квадрата, маємо:
Піднісши ліву та праву частину останньої рівності до квадрата, маємо:  Оскільки R є невід’ємною величиною, то з останнього рівняння отримуємо: R = 1000 (Ом).
Оскільки R є невід’ємною величиною, то з останнього рівняння отримуємо: R = 1000 (Ом).
Через прикладні задачі можна привести учнів до самостійного формування поняття показникового рівняння.
Задача 5. Після скількох періодів піврозпаду з 64 градіоактивної речовини залишиться 8 г?
Розв’язання. Учитель повідомляє учням рівняння радіоактивного розпаду, з яким вони будуть мати справу в курсі фізики 11 класу: 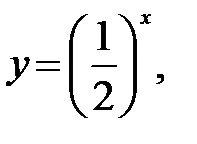 де y – частина речовини, яка залишається внаслідок розпаду після х періодів піврозпаду. Учні одержують математичну модель даної задачі у вигляді рівняння:
де y – частина речовини, яка залишається внаслідок розпаду після х періодів піврозпаду. Учні одержують математичну модель даної задачі у вигляді рівняння: 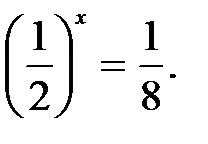
Аналіз даної задачі приводить до висновку, що існують рівняння, у яких невідоме входить до показників степенів при сталих основах, і саме такі рівняння називають показниковими.
Усвідомленню учнями ролі показникових рівнянь як математичних моделей певних реальних явищ і процесів сприятиме розв’язування наступної задачі.
Задача 6. Під час розкопок знайдено рештки тварини, питома радіоактивність  яких (А) становила 5,1 розпадів/хв на 1 г речовини. У сучасних умовах питома радіоактивність
яких (А) становила 5,1 розпадів/хв на 1 г речовини. У сучасних умовах питома радіоактивність 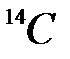 організмів
організмів  дорівнює 15,3 розпадів/хв на 1 г речовини. Який вік викопаної тварини, якщо період напіврозпаду
дорівнює 15,3 розпадів/хв на 1 г речовини. Який вік викопаної тварини, якщо період напіврозпаду 
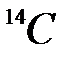 дорівнює 5668 років? Вказівка: застосовувати закон зміни радіоактивності в часі:
дорівнює 5668 років? Вказівка: застосовувати закон зміни радіоактивності в часі: 
До поняття логарифмічного рівняння приводить учнів розв’язування наступної задачі.
Задача 7. Барабанна перетинка людини розривається, якщо рівень інтенсивності звуку  дБ. Визначити інтенсивність звукового тиску (I), за якого може розірватись барабанна перетинка.
дБ. Визначити інтенсивність звукового тиску (I), за якого може розірватись барабанна перетинка.
Розв’язання. Рівень інтенсивності звуку визначається за формулою  У даному випадку для барабанної перетинки людини поріг чутності
У даному випадку для барабанної перетинки людини поріг чутності 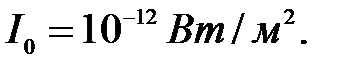 Підставивши значення
Підставивши значення 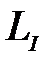 та
та  отримуємо рівняння:
отримуємо рівняння:  Учитель звертає увагу учнів на те, що змінна в цьому рівняння міститься під знаком логарифма. Такі рівняння називають логарифмічними.
Учитель звертає увагу учнів на те, що змінна в цьому рівняння міститься під знаком логарифма. Такі рівняння називають логарифмічними.
Нами дібрана низка прикладних задач, що може бути використана в класах різних профілів для усвідомлення учнями ролі тригонометричних, ірраціональних, показникових та логарифмічних рівнянь та для аналізу набуття ними відповідних предметних компетентностей. Ця добірка наведена у Додатку Н.
Кожен із окреслених етапів є вкрай важливим для розв’язання задачі та особливо для навчання розв’язувати задачі.
Під час розгляду прикладних задач на уроках доцільно поєднувати фронтальну, групову та індивідуальну форми роботи, пропонувати учням самостійні роботи навчального характеру. Для організації групової роботи учням пропонуються завдання, спрямовані на формування в них здатності застосовувати розглянуті процедури.
Таким чином, розв’язуючи прикладні задачі, вчитель повинен слідкувати , щоб учні дотримувалися орієнтовної основи дій.
Уроки з використанням прикладних задач слід планувати як підсумкові в кожній темі і проводити їх у всіх 10-11 класах незалежно від профілю навчання. Обов’язково включати ці задачі в підсумкові контрольні роботи. Як такі, що формують процедурну, логічну, конструктивно-графічну, дослідницьку та методологічну компетентність, що є складовими предметної компетентності.
Отже, виконання зазначеної умови надасть можливість вчителю не тільки зацікавити школярів фізико-математичними дисциплінами, залучити їх до виконання цікавих завдань, переконати у необхідності і цінності здобутих ними знань, а й сформувати предметну компетентність.
Наступною дидактичною умовою для формування предметної компетентності старшокласників у процесі вивчення предметів фізико-математичного циклу є застосування інформаційно-комунікативних технологій на уроках фізики й математики. Метою використання інформаційно-комунікативних технологій на уроках фізики й математики є створення на уроках предметів фізико-математичного циклу умов для свідомої активної участі старшокласників у творчій діяльності за рахунок підвищення ефективності викладання цих дисциплін через використання ІКТ.
Як уже зазначалося, використання ІКТ сприяє формуванню ключових, галузевих та предметних компетентностей учнів. Під час вивчення математики й фізики використання ІКТ сприяє формуванню в учнів процедурної, логічної, конструктивно-графічної та дослідницької компетентностей, як складових предметної компетентності. При цьому як засвідчив педагогічний експеримент доцільно систематично використовувати ІКТ на уроках математики й фізики.
В процесі викладання предметів фізико-математичного циклу вчитель може застосовувати табличний редактор MS Excel; програмне забезпечення Microsoft Office; програми для створення презентацій Microsoft PowerPoint; електронно-методичні комплекси GRAN-1, GRAN-2, GRAN-3, MacromediaFlash, AdobeFlash.; Інтернет-відео та фотоматеріали; Інтернет – ресурсів тощо.Кожен елемент із зазначеного переліку програмних засобів є достатньо досконалим у своєму роді. Використовуючи їх на уроці по черзі або разом, можна значною мірою підвищити ефективність навчально-виховного процесу.
Презентація Microsoft PowerPoint є універсальним видом наочності і може бути застосованою на уроці будь-якого типу. Та найефективнішим є підготовка та використання презентацій на таких етапах вивчення математики й фізики:
- на уроках вивчення нового матеріалу у вигляді комп’ютерного діафільму з використанням елементів анімації;
- на уроках узагальнення і систематизації знань з теми - у вигляді шаблону «навчальний посібник» (презентації з майстра автозмісту) або йому подібного, у якому розглядаються всі поняття, формули, співвідношення з теми, приведено матеріал з історії розвитку поняття, міститься яскравий ілюстративний матеріал – діаграми, схеми, ілюстрації, аудіо та відеофайли, матеріали для контролю та самоконтролю знань.
Як зазначалося в п.2.2 програмні засоби використовуються у трьох напрямах: ілюстративному, схематичному та інтерактивному. Схематичний метод дозволяє скористатися можливостями комп’ютерних програм для побудови структурно – логічних схем та опорних конспектів. Після комп’ютерної обробки опорні конспекти стають більш наочними, цікавими. Цьому допомагає прикладна програма Power Point. Мультимедійні засоби навчання допомагають посилити мотивацію навчання, урізноманітнити форми подання інформації, посилити співтворчість учителя та учня на уроці, розширити самостійність учня. Деякі розробки презентацій, уроків, заходів розміщено у додатку Н1.
Учні 9-го класу вивчають з інформатики тему «Електронні таблиці»,тому доцільним буде використання школярами 10-11 класів табличного редактора MS Excel для обчислення тих чи інших значень за допомогою заданих формул. Під час вивчення тем «Функції. Графіки функцій» та «Перетворення графіків функцій» доцільно використовувати програмні продукти для побудови графіків функцій. Насамперед є можливість зекономити час, а натомість розв’язати більшу кількість завдань. Використовуючи готові графіки, не важко навчити учнів «читати» властивості відповідних функцій: проміжки монотонності, знакосталості, точки екстремуму, розв’язувати нерівності f(x) <0 (f(x) >0), бачити наочно перетворення графіків функцій тощо.
Розглянемо приклади використання ІКТ на уроках фізико-математичного циклу.
Для ефективно використовувати ІКТ для розв’язування рівнянь та нерівностей, доцільно вже під час вивчення тригонометричних функцій познайомити учнів із навчальними математичними пакетами, наприклад, із ППЗ “GRAN1D” і навчити їх будувати та аналізувати графіки функцій. Для цього можна запропонувати учням наступне завдання: побудувати у ППЗ “GRAN1D” графік функції 
Розв’язування. Учні заходять у меню “Об’єкт” – “Створити” і створюють об’єкт типу “Явна: Y = Y(X)” з аналітичним виразом виду y = sin(x) + cos(x). Потім заходять у меню “Графік” – “Побудувати” та отримують у вікні “Графік” графік функції f(x) (рис. 2.9).

Рис. 2.9. Графік функції f(x) = sin(x) + cos(x) побудований у ППЗ “GRAN1D”
Після цього доцільно згадати, що 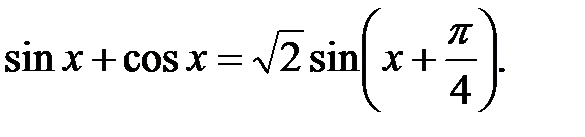 За допомогою елементарних перетворень графіка функції sin x учні будують графік функції f(x) та порівнюють його із графіком отриманим за допомогою комп’ютера.
За допомогою елементарних перетворень графіка функції sin x учні будують графік функції f(x) та порівнюють його із графіком отриманим за допомогою комп’ютера.
Доцільним є використання ППЗ “GRAN1D ” у процесі ознайомлення учнів із орієнтовними основами розв’язування рівнянь та нерівностей за допомогою властивостей функцій. У таблиці Р.1 Додатку Р.1 наведені приклади розв’язування рівнянь із використанням вище зазначених орієнтовних основ та графічна ілюстрація у ППЗ “GRAN1D”.
Під час вивчення тригонометричних, ірраціональних, показникових і логарифмічних рівнянь та нерівностей доцільно пропонувати учням наступні завдання.
1. Розв’язати нерівність 
Розв’язування. Учні заходять у меню «Об’єкт» – «Створити» і створюють об’єкт типу «Явна: Y = Y(X)» з аналітичним виразом виду y = Log(3, x). Потім заходять у меню «Графік» – «Побудувати» та отримують у вікні «Графік»графік функції f(x). Після цього учні заходять у меню «Операції» – «Нерівності»«C-ма нерівностей y(x) < (>) с», на екрані з’являється табличка (рис. 2.10), у якій учні вибирають знак нерівності (у даному випадку «>») та число (у даному випадку 1), більше (менше) якого функція Y(X). У результаті цих дій у вікні «Графік» з’являється графічне розв’язування заданої нерівності (рис.2.10). Але у даному випадку графічне розв’язування обмежене границями, у яких побудовано графік функції у вікні «Графік». За наведеним рисунком маємо, що розв’язком нерівності є інтервал від 3 до 20. Тому необхідно запропонувати учням уточнити отриманий на екрані розв’язок. Оскільки  є функцією зростаючою, а
є функцією зростаючою, а  сталою, вони можуть перетинатися дише в одній точці (ми вже визначили, що це точка з абсцисою 3). На основі цих міркувань учні доходять висновку, що розв’язком даної нерівності є проміжок
сталою, вони можуть перетинатися дише в одній точці (ми вже визначили, що це точка з абсцисою 3). На основі цих міркувань учні доходять висновку, що розв’язком даної нерівності є проміжок 

| 
|
Рис. 2.10. Розв’язування нерівності  за допомогою ППЗ “GRAN1D” за допомогою ППЗ “GRAN1D”
|
Під час уроків розв’язування рівнянь та нерівностей з використанням ІКТ доцільно запропонувати учням наступний орієнтир: якщо за умовою завдання вимагається знайти кількість коренів рівняння, то доцільно застосовувати графічний метод розв’язування.
Читайте також:
- I. Актуалізація знань учнів
- I. ІСТОРИЧНІ ШЛЯХИ ФОРМУВАННЯ УКРАЇНСЬКОЇ КУЛЬТУРИ
- I. Контроль і закріплення знань учнів
- II. Актуалізація опорних знань і вмінь учнів
- II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ І ВМІНЬ УЧНІВ
- II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ І ВМІНЬ УЧНІВ
- II. Розвиток математичних знань учнів.
- II. Розвиток математичних умінь учнів
- II. Розвиток математичних умінь учнів
- II. Розвиток математичних умінь учнів
- II. Розвиток математичних умінь учнів
- III. Актуалізація опорних знань учнів.
| <== попередня сторінка | | | наступна сторінка ==> |
| Дидактичні умови формування предметної компетентності старшокласників у процесі вивчення предметів фізико-математичного циклу | | | Розглянемо приклади використання програми Microsoft Office Excel на уроках фізики в 10класі. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |