• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

В) добуток синусів і косинусів.

CosL*cosB= ½(cos(L-B)+cos(L+B)).

cosL*sinB=1/2(sin(L-B)+sin(L+B))

sinL*sinB= ½(cos(L-B)-cos(L+B))

Дані формули дозволяють представити добутки sin і cos у вигляді лінійної комбінації тих же функцій, але з другими аргументами.

64.Визначений інтеграл, як границя інтегральної суми. Теорема існування. Геометричний зміст визначеного інтеграла.

Скінченна границя інтегральної суми, при умові, що число відрізків n прямує до нескінченності, а довжина найбільшого з них прямує до 0 наз. Визначеним інтегралом функції y = f(x) в межах х = а, х = в і позначається

Теорема існування визначеного інтегралу.

Якщо функція y = f(x) визначена на відрізку [a,b] або має на цьому відрізку лише точки скінченого розриву, то визначений інтеграл існує для цієї функції і він єдиний.

Геометричний зміст визначеного інтегралу.

Нехай дано функцію y = f(x),яка визначена на відрізку [a,b], причому f(x)>=0. Потрібно знайти S криволінійної трапеції аАВв, обмеженою лініями х = а, х = в, у = 0, у= f(x)/

Малюнок

1). Розіб’ємо відрізок АВ на n частин точками Хі, і=0, а = Х0<X1<X2<Xn= в.

2). Позначимо через дельта Х = Хі+1 –Хі .

3). В кожному з відрізків [ Xi-1 +Xi], виберемо довільну точку Ei [ Xi-1, Xi] і обчислемо

4). В кожному частинному проміжку побудуємо прямокутник, висота якого є , а основа (дельта) Хі.

5). Визначимо суму

65.Властивості визначеного інтеграла.

1. Сталий множник можна винести за знак інтеграла.

2.Визначений інтеграл від алгебраїчної суми скінченого числа неперервних функцій дорівнює сумі їх інтегралів.

3.Визначений інтеграл з однаковими межами інтегрування = 0.

4.Якщо у визначеному інтегралі поміняти місцями межі інтегрування , то знак перед інтегралом зміниться на протилежний.

5. Для любих чисел а ,в ,с справедлива рівність:

6. Якщо функція f(x) і g(x) неперервні на відрізку [ a ,b] , f(x)>=g(x), то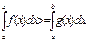

7.Якщо m і M найменше і найбільше значення функції на відрізку [a, b], то знаходиться в межах: m(b-a) <= 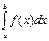<= M(b-a).

8. Якщо функція y = f(x) на [a,b] неперервна, то існує така точка С є[a,b], що f( c) = .

66.Визначений інтеграл із змінною, верхньою межею і його похідна на поверхній межі. Нехай y=f(x) неперервна на відрізку [a,b] , тоді визначений інтеграл існує і дорівнює деякому числу. Якщо в інтегралі нижню межу «а» зафіксувати, а «б» - замінити змінною х, де х є [a,b], то одержимо: (2). Змінною інтегрування ми позначимо буквою t, щоб відрізнити її від змінної верхньої межі. Інтеграл (2) буде залежать від положення т.Х, тобто інтеграл(2) є деяка функція своєї верхньої межі.

Теорема:

Нехай функція f(t) неперервна скрізь на проміжку [a,x], тоді похідна від визначеного інтегралу по змінній верхній межі х дорівнює підінтегральній функції в якій змінна інтегрування замінена цією межею.

Читайте також:

1. В) добуток синусів і косинусів.
2. Векторний добуток векторів
3. Векторний добуток векторів і його властивості. Геометричні застосування векторного добутку.
4. Векторний добуток векторів.
5. Векторний добуток і його властивості.
6. Вуглевидобуток в Україні та перспективи його розвитку
7. Г) видобуток і промисел живих ресурсів моря з метою їх раціо-
8. Де - місячний видобуток руди у кар’єрі, млн.т.
9. Декартів добуток
10. Декартів добуток двох множин. Зображення декартового добутку двох числових множин на координатній площині
11. Декартовий (прямий) добуток множин

Переглядів: 773