
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
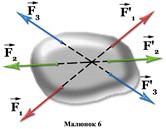
Геометричний метод складання сил
Мета
Вступ
Мета
Переробка зерна на крупу
Виробляються такі види і сорти круп:
– з гречки – крупа пропарена і непропарена (ядриця) I і II сортів, крупа продільна і дієтичне борошно;
– з рису – рис шліфований і полірований вищого, I і II сортів, рис дроблений;
– з гороху – горох лущений, полірований (цілий або поколений) і крупа типу манної;
– з проса – пшоно шліфоване вищого, I і II сортів;
– з вівса – пластівці, крупа недроблена пропарена, крупа плющена вищого і I сортів, толокно;
– з ячменю – крупа перлову 15 – номерна;
– з кукурудзи – крупа шліфована 5-номерна, крупа для пластівців і кукурудзяних паличок;
– з пшениці – манна крупа.
Технологічний процес виробництва круп має таку схему:
| При переробці гречки виходить 45% ядриці I сорту, 15 – II, 10 – проділу, до 5% борошенця. На лузгу припадає 21%, кормові відходи – 3, некормові – 0,5%. При виробництві пшона його вихід становить 68,5%, 5,5% борошенця, 18% лузги, 7 – кормових і 0,5% некормових відходів. З ячменю виробляють 78% крупи, 6% борошенця, 10% плівок, 5 – кормових і 0,5% - некормових відходів. | ||||||||
| Очищення партії зерна ві домішок | ||||||||
| Сортування очищеного зерна за крупністю | ||||||||
| Лущення | ||||||||
| Відокремлення зерна від плівок | ||||||||
| Обробка зерна | ||||||||
| Сортування готової продукції | ||||||||
Навчальна: ознайомити з основним поняттями та аксіомами статики; з поняттями про реакції в'язей та їх напрямок.
Виховна : виховання інтересу до навчальної дисципліни «Технічна механіка».
План лекції:
1 Вступ
1.1 Зміст і значення предмету «Технічна механіка»
1.2 Зміст розділу «Теоретична механіка»
2 Механічний рух. Рівновага. Матеріальна точка
3 Абсолютно тверді тіла
4 Сила. Сили механіки
5 Аксіоми статики
6 В'язі та їх реакції
7 Основні типи в`язей
1.1 Зміст і значення предмету «Технічна механіка»
«Основи технічної механіки» містять комплекс найважливіших загально технічних знань і включає три розділи: теоретична механіка; основи опору матеріалів; деталі механізмів і машин.
Вивчення технічної механіки використовують навички для постановки і рішення прикладних задач. Цим обумовлене важливе значення технічної механіки як основи для вивчення спеціальних дисциплін.
Механіка — це наука про механічний рух і взаємодію матеріальних тіл.
Основна властивість матерії полягає в тому, що вона знаходиться в безперервному русі. Представляє необмежені в просторі і нескінченні в часі різні форми руху матерії, починаючи від механічного переміщення і взаємодії тіл і кінчаючи мисленням і розвитком суспільства.
Механіка вивчає тільки одну форму руху матерії — механічний рух. Інші форми руху містять в собі механічний рух, але не можуть бути пояснені одними законами механіки і являються об'єктом вивчення інших наук, наприклад хімії, біології і т.д.
Механіка є однією з найстародавніших наук. Термін «механіка» введений видатним філософом старовини Аристотелем (384—322 до н. е.). Перші наукові основи вчення про рівновагу тіл містяться в працях Архімеда (287—212 до н. е.). На всіх етапах свого розвитку механіка була тісно пов'язана з розвитком продуктивних сил суспільства і сприяла технічному прогресу.
1.2 Зміст розділу «Теоретична механіка»
Теоретична механіка — це розділ механіки, в якому вивчаються закони руху тіл і загальні властивості цих рухів.
Теоретична механіка включає статику, кінематику і динаміку.
2 Механічний рух. Рівновага. Матеріальна точка
Механічний рух - зміна з часом положення тіла в просторі відносно інших тіл.
Окремим випадком механічного руху є стан спокою. Спокій і механічний рух завжди мають відносний характер, оскільки тіло, що покоїться, розглядається як нерухоме по відношенню до деякого іншого тіла, яке, у свою чергу, може переміщатися в просторі. Так, людина, що сидить у вагоні, може вважати себе таким, що знаходиться у спокої по відношенню до вагону, але по відношенню до Землі він перебуватиме в русі. Наприклад, ми говоримо, що станина машини або фундамент споруди знаходиться у спокої. Вони дійсно нерухомі щодо Землі, але разом з нею скоюють складний рух навколо Сонця.
Абсолютно нерухомих тіл в природі немає.
Статика є частина теоретичної механіки, що вивчає умови, при яких тіло знаходиться в рівновазі. Рівновагою вважатимемо такий стан, коли тіло знаходиться у спокої або рухається прямолінійно і рівномірно.
Рівновага тіла - стан тіла, коли воно знаходиться у спокої або рухається прямолінійно і рівномірно.
Тіло можна розглядати як матеріальну точку, тобто його можна представити геометричною точкою, в якій зосереджена вся маса тіла, у тому випадку, коли розміри тіла не мають значення в даній задачі.
Матеріальною точкою називається точка, що має масу.
Наприклад, при вивченні руху планет і супутників їх вважають матеріальними точками, оскільки розміри планет і супутників досить малі в порівнянні з розмірами їх орбіт.

З другого боку, вивчаючи рух планети (наприклад, Землі) навколо осі, її вже не можна вважати матеріальною точкою.
Тіло можна вважати матеріальною точкою у всіх випадках, коли всі його точки здійснюють тотожні рухи, тобто тіло рухається поступально.
Поступальний рух – рух при якому всі точки тіла рухаються паралельно одна одній тобто однаково.

Тіло можна розглядати як матеріальну точку в наступних випадках:
1 Коли розміри тіла набагато менше переміщення яке здійснює дане тіло;
2 Тіло рухається поступально.
3 Абсолютно тверді тіла
Розглядаючи рівновагу тіл, їх вважають абсолютно твердими (або абсолютно жорсткими), тобто припускають, що ніякі зовнішні дії не викликають зміни їх розмірів і
форми і що відстань між будь-якими двома точками тіла завжди залишається незмінною.
Абсолютно тверде тіло – це тіло у якого відстань між будь-якими двома точками тіла завжди залишається незмінною.
Всяке тіло можна вважати взаємозв'язаною сукупністю матеріальних точок.
Абсолютно тверде тіло є незмінною системою матеріальних точок.
Насправді всі тіла під впливом силових дій з боку інших тіл деформуються і змінюють свої розміри або форму. Але матеріали, форму і розміри елементів конструкцій підбирають з таким розрахунком, щоб їх деформації були мінімальними, тому такими деформаціями нехтують і розглядають елементи конструкцій як абсолютно тверді тіла.
4 Сила. Сили механіки
Тіла в природі різним чином взаємодіють між собою або з навколишнім їх середовищем. Механічна взаємодія тіл, тобто взаємодія, що впливає на їх стан спокою або руху (механічний стан), характеризується силами. У механіці розрізняють сили тертя, пружності і гравітаційні сили. Сила тяжіння відноситься до гравітаційних сил, а вага до сил пружності.
Сила є міра механічної взаємодії тіл.
Сила характеризується трьома елементами: числовим значенням (модулем), напрямом і точкою прикладення.
Таким чином, сила — величина векторна. Числове значення сили називається модулем сили. Напрям сили є напрямнаправлення того руху, який отримала б вільна матеріальна точка, що покоїться, під дією цієї сили. Пряма лінія, по якій спрямований вектор сили, називається лінією дії сили.
Як відомо з фізики, в Міжнародної системі одиниць (СІ) одиницею вимірювання модуля сили являється ньютон (Н).
Досі іноді використовують для вимірювання сил технічну систему (МКГСС), в якій як одиниця сили застосовується кілограм-сила (кгс). Одиниці сили в системах СІ і МКГСС зв'язані співвідношенням 1 кгс = 9,81 Н. При допустимих наближених розрахунках можна вважати 1 Н ≈ 0,1 кгс, що дає похибку, приблизно 2%.
Вектор сили зображається відрізком, на кінці якого ставиться стрілка. Стрілка указує напрям вектора, довжина відрізка — значення вектора, виміряне у вибраному масштабі.
Вектор позначають однією буквою із стрілкою нагорі 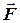 ,
,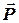 ,
,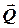 , а модуль сили позначають без стрілки F, P, Q.
, а модуль сили позначають без стрілки F, P, Q.
| |
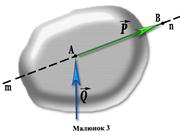
Системою сил називають сукупність декількох сил, прикладених до тіла, точки або системи тіл і точок.
5 Аксіоми статики
Умови, при яких тіло може знаходитись в рівновазі, виводять з декількох основних положень, що приймаються без доказів, але підтверджених дослідом і званих аксіомами статики.
Перша аксіомавизначає зрівноважену систему сил. Система сил, прикладена до матеріальної точки, є зрівноваженою, якщо під її дією точка знаходиться в стані відносного спокою або рухається рівномірно і прямолінійно (тобто за інерцією).
Розглядаючи першу аксіому, неважко встановити, що зрівноважена система сил як причина механічного руху еквівалентна нулю.
Тіло (на відміну від точки) під дією зрівноваженої системи не завжди знаходиться у спокої або рухається рівномірно і прямолінійно. Можливий випадок, коли врівноважена система сил, а точніше врівноважена система пар сил викликає рівномірне обертання тіла навколо деякої нерухомої вісі.
Друга аксіомавстановлює умову рівноваги двох сил. Дві рівні по модулю сили (F1 = F2), прикладені до абсолютно твердого тіла і направлені по одній прямій в протилежні сторони, взаємно врівноважуються.
| |
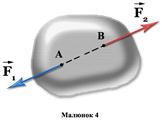
Дві системи сил еквівалентні,якщо узяті окремо вони роблять однакову механічну дію на тіло.
Слід відмітити, що еквівалентні системи сил можуть викликати різні деформації нетвердого тіла.
Дві еквівалентні системи сил, що окремо діють на один і той же стержень АВ, причому Р1 = Р2, а Q1 = Q2. Але система сил (Р1, Р2) прагне стиснути стержень, а система сил (Q1, Q2) — розтягнути його.
Еквівалентність систем сил записуються так: (Р1, Р2) ≡ (Q1, Q2).
| |
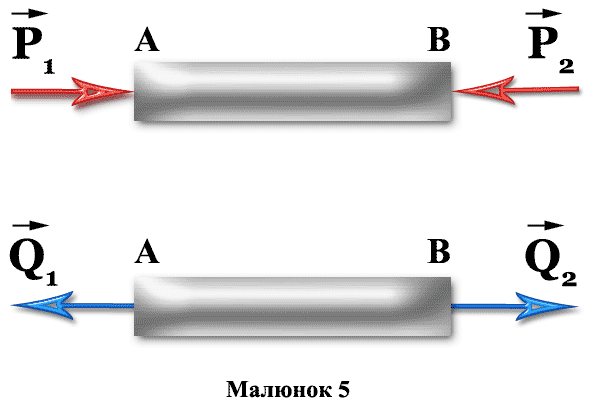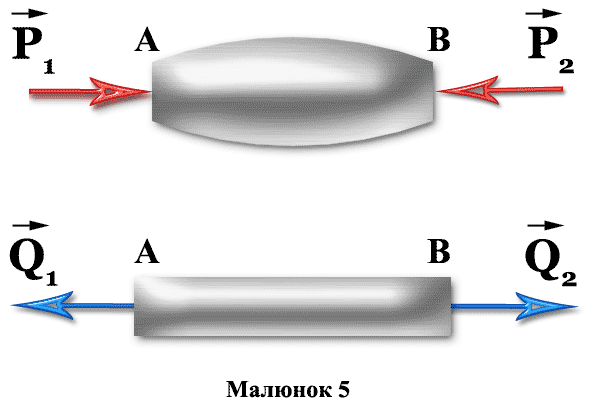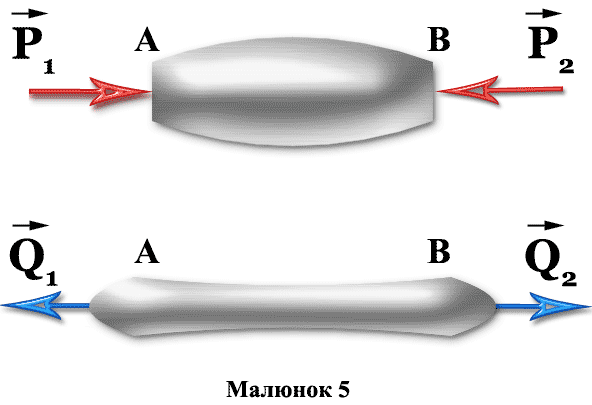
Будь-яку складну систему сил завжди можна замінити більш простою еквівалентної їй системою сил. Одну силу, еквівалентну даній системі сил, називають рівнодійною цієї системи. Рівнодійна - одна сила, що еквівалентна даній системі сил.
Силу, рівну по модулю рівнодіючої і направлену по тій же лінії дії, але в протилежну сторону, називають врівноважуючою силою. Якщо до системи сил додана врівноважуюча сила, то отримана нова система знаходиться в рівновазі і, як зазначено вище, еквівалентна нулю.
Врівноважуюча сила - сила рівна по модулю рівнодійній і направлена по тій же лінії, але в протилежну сторону.
Третя аксіомаслужить основою для перетворення сил. Не порушуючи механічного стану абсолютно твердого тіла, до нього можна прикласти або відкинути від нього зрівноважену систему сил. Аналогічний ефект вийде при відкиданні цих врівноважених сил.
| |
З другої аксіоми витікає наслідок, згідно якому всяку силу, діючу на абсолютно тверде тіло, можна перенести уздовж лінії її дії в будь-яку точку тіла, не порушивши при цьому його механічного стану.
Вектори, які можна переносити по лінії їх дії, називають ковзними.
Сила є ковзним вектором.
Четверта аксіомавизначає правило складання двох сил. Рівнодійна двох сил, прикладених до однієї точки, прикладена в цій точки і є діагоналлю паралелограма, побудованого на даних силах.
| |
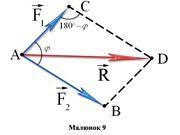
Визначення рівнодійної двох сил за правилом паралелограма називається векторним, або геометричним, додаванням і виражається векторною рівністю

Модуль рівнодійної двох сил можна визначити за формулою
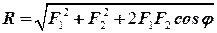
При графічному визначенні рівнодійної двох сил замість правила паралелограма можна користуватися правилом трикутника.
| |

П'ята аксіомавстановлює, що в природі не може бути односторонньої дії сили. При взаємодії тіл будь-якій дії відповідає рівна і протилежно спрямована протидія.
| |
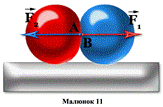
Дія і протидія завжди прикладена до різних тіл, і саме тому вони не можуть врівноважуватися.
6 В'язі та їх реакції
Тіла, що розглядаються в механіці можуть бути вільними і невільними.
Вільним називають тіло, яке не зазнає ніяких перешкод для переміщення в просторі в будь-якому напрямі. Якщо ж тіло зв’язано з іншими тілами, які обмежують його рух в одному або декількох напрямах, то воно є невільним.Тіла, які обмежують рух даного тіла, називають в'язями.
В'язь - тіло, що обмежує рух даного тіла.
При взаємодії між тілом і його в'язями виникають сили, протидіючі можливим рухам тіла. Ці сили діють на тіло з боку в'язів і називаються реакціями в’язів.
Реакція в'язі - це сила, що діє на тіло з боку в'язі.
Реакція в'язі завжди протилежна тому напряму, по якому в'язь перешкоджає руху тіла. Існування реакцій обґрунтовується аксіомою про дію і протидію. Для визначення реакцій в'язей використовують принцип звільнення від в'язів. Не змінюючи рівноваги тіла, кожну в'язь можна відкинути, замінивши її реакцією.
7 Основні типи в`язей
Визначення реакцій в'язей є однією з найважливіших задач статики. Нижче приведені найпоширеніші види в'язей, що зустрічаються в задачах:
1 Гладка опорна поверхня. В цьому випадку реакція 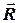 в’язі завжди спрямована по нормалі до опорної поверхні.
в’язі завжди спрямована по нормалі до опорної поверхні.
| |
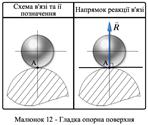
2 Опора на гладке ребро тіла або тіло опирається на гладку поверхню. Коли одна з поверхонь, що дотикаються, є точкою, то реакція направлена по нормалі до другої поверхні.
| |
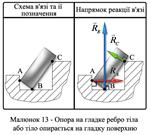
3 Шарнірно-рухома опора (коткова опора) дозволяє поворот навколо осі шарніра і переміщення вздовж опорної поверхні. Реакція в'язі перпендикулярно до опорної площини.
| |
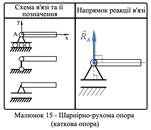
4 Шарнірно-нерухома опора (циліндричний шарнір). Реакція лежить в площині, перпендикулярній до осі обертання, але напрямок її невідомий. Тому при розв’язані задач її замінюють складовими 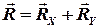
| |

5 Шорстка площина. Напрямок такої в'язі також невідомий, тому її розкладають на нормальну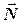 і дотичну
і дотичну  (сила тертя), тобто
(сила тертя), тобто 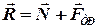 .
.
| |

6 Гнучка в'язь (нитка, дріт, ланцюг, канат, мотузка).Реакція цієї в'язі прикладена в точці кріплення і направлена вздовж в’язі до точки підвішування.
| |

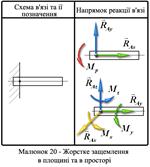
7 Защемлення (жорстке закладання) - це спосіб закріплення балок в стінах будинків. Невідомими залишаються напрям і величина реакції. При розв'язуванні задач таку в'язь замінюють трьома невідомими реакції і трьома невідомими складовими реактивного моменту.
| |
Домашнє завдання:
1Вивчити[І] § 1 - 10.
8 Контрольні запитання
8.1 Що таке матеріальна точка?
8.2 Що таке абсолютно тверде тіло?
8.3 Що таке сила?
8.4 Яка одиниця вимірювання сили?
8.5 Що таке система сил?
8.6 Які системи сил називаються еквівалентними?
8.7 Що таке рівнодійна та врівноважуючи сили? В чому їх схожість та різниця?
8.8 Сформулюйте аксіоми статики.
8.9 Що таке в’язь, реакція в’язів, їх напрямок у кожному конкретному випадку?
8.10 Яка система називається плоскою?
ЛЕКЦІЯ №2 - ПЛОСКА СИСТЕМА ЗБІЖНИХ СИЛ (ПСЗС)(2години)
Навчальна: ознайомитися з поняттями про плоску систему збіжних сил; умовами рівноваги; алгоритмом розв’язання задач на плоску систему збіжних сил.
Виховна : виховання інтересу до навчальної дисципліни «Технічна механіка».
План лекції:
1 Геометричний метод складання сил;
2 Проекція сили на вісь;
3 Проекція векторної суми на вісь;
4 Рівняння рівноваги плоскої системи збіжних сил;
5 Алгоритм рішення задач на плоску систему збіжних сил.
Збіжними силами називають сили лінії дії яких перетинаються в одній точці.
Силу можна переносити по лінії її дії, тому збіжні сили завжди можна перенести в одну точку — в точку перетину їх ліній дії.


Знайти рівнодійну цих сил можна послідовно додавши їх правилом трикутника, але зручніші побудувати силовий многокутник. Для цього послідовно перемістити їх паралельним переносом щоб кінець однієї сили співпадав з початком іншої. А потім початок першої сили з'єднати з кінцем останньої.
Отримана фігура називається силовим многокутником, а замикаюча сторона є сумою даних векторів, тобто рівнодійною силою.
| |

Іншими словами, вектор рівнодійної сили завжди спрямована назустріч обходу багатокутника, відповідному послідовному складанню заданих сил.
Коли при побудові силового багатокутника кінець останньої складової сили поєднається з початком першою, рівнодійна системи збіжних сил буде дорівнювати
нулю, то в цьому випадку система збіжних сил знаходиться в рівновазі.
| |

2 Проекція сили на вісь
Рішення задач на рівновагу збіжних сил, за допомогою побудови замкнутих силових багатокутників в більшості випадків зв'язано з громіздкими побудовами. Більш загальним і універсальним методом рішення таких задач є перехід до визначення проекцій заданих сил на координатні осі і операцію з цими проекціями. Віссю називають пряму лінію, якій приписаний певний напрям.
Проекція вектора на вісь є скалярною величиною, яка визначається відрізком осі, що відсікається перпендикулярами, опущеними на неї з початку і кінця вектора.
Проекція вектора вважається додатною (+), якщо напрям від початку проекції до її кінця співпадає з позитивним напрямом осі.
Проекція вектора вважається від'ємною (—), якщо напрям від початку проекції до її кінця протилежно позитивному напряму осі.
Розглянемо ряд випадків проектування сил на вісь:
1 Вектор сили складає з додатним напрямом осі х гострий кут α:
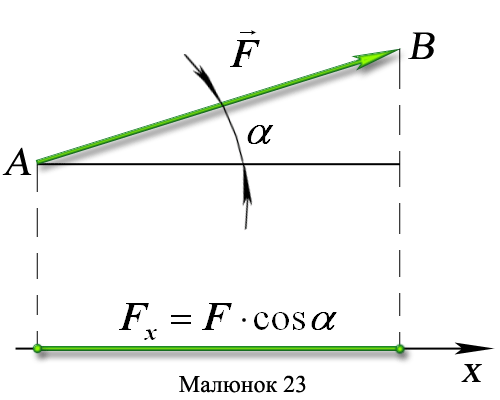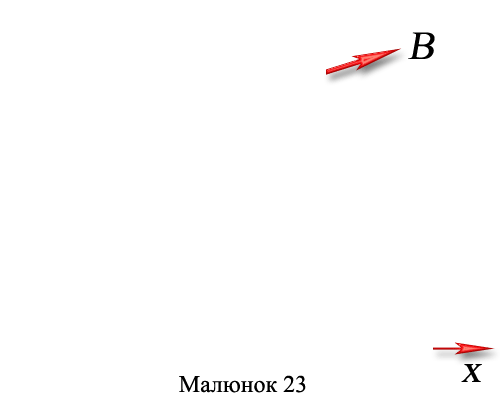
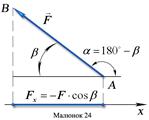
2 Сила складає з додатним напрямом осі х тупий кут α:
| |
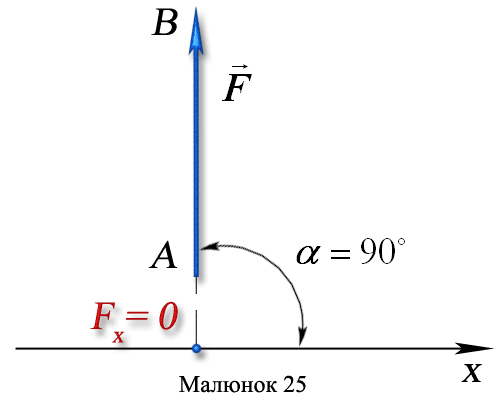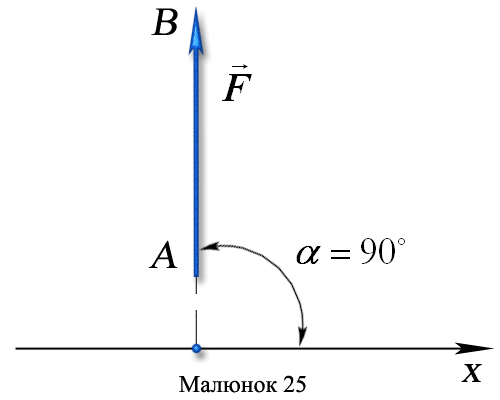
3 Сила перпендикулярна осі х:
| |
4 Сила паралельна осі х:
| |
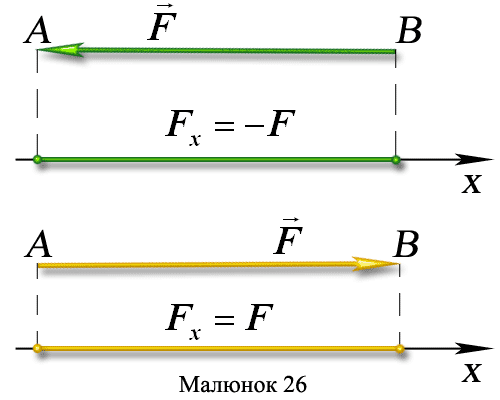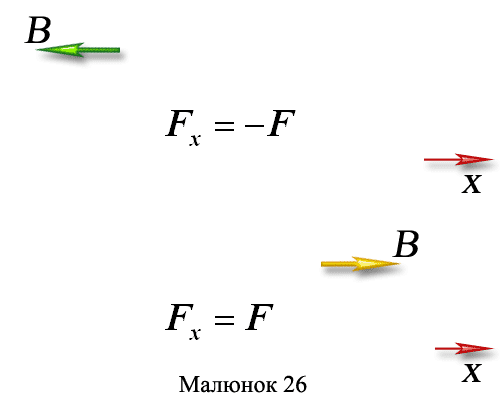
Отже, проекція сили на вісь координат рівна добутку модуля сили на косинус кута між вектором сили і додатним напрямом осі.
3 Проекція векторної суми на вісь
Проекція векторної суми або рівнодійної на будь-яку ось рівна алгебраїчної сумі проекцій складових векторів, на ту ж ось.

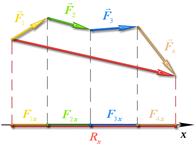
У площині геометричну суму сил можна спроектувати на дві координатні осі, а в просторі — відповідно на три.
4 Рівняння рівноваги плоскої системи збіжних сил
4.1 Геометрична умова рівноваги ПСЗС
ПСЗС знаходиться в рівновазі, якщо силовий многокутник даний сил замкнутий.
4.2 Аналітична умова рівноваги ПСЗС
ПСЗС знаходиться в рівновазі, якщо алгебраїчна сума проекцій сил цієї системи на дві взаємно перпендикулярні осі дорівнювали нулю.

де 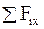 - сума проекцій всіх сил на вісь х;
- сума проекцій всіх сил на вісь х;
 - сума проекцій всіх сил на вісь у.
- сума проекцій всіх сил на вісь у.
5 Алгоритм рішення задач на плоску систему збіжних сил.
1 Виділяємо об'єкт рівноваги - точка, де сходяться лінії дії всіх сил (центр сил).
2 Відкидаємо в'язі та замінюємо їх дію реакціями в'язей.
3 Вибираємо раціональну систему координат.
4 Складаємо розрахункову схему.
5 Записуємо рівняння рівноваги та складаємо умови рівня рівноваги плоскої системи збіжних сил:

де 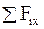 - сума проекцій всіх сил на вісь х;
- сума проекцій всіх сил на вісь х;
 - сума проекцій всіх сил на вісь у.
- сума проекцій всіх сил на вісь у.
6 Розв'язуємо отримані рівняння відносно невідомих.
7 Виконуємо перевірку(графічним методом).
8 Робимо висновок про отримані результати.
Домашнє завдання:
1Вивчити[І] § 12 - 18.
6 Контрольні запитання
6.1 Яка система називається плоскою системою збіжних сил?
6.2 Як визначити рівнодійну ПСЗС графічним методом?
6.3 Сформулювати аналітичну умову рівноваги ПСЗС?
ЛЕКЦІЯ №3 – ПАРА СИЛ(2години)
Читайте також:
- D) методу мозкового штурму.
- H) інноваційний менеджмент – це сукупність організаційно-економічних методів управління всіма стадіями інноваційного процесу.
- I Метод Шеннона-Фано
- I. Метод рiвних вiдрiзкiв.
- II. Вимоги до складання паспорта бюджетної програми
- VII. Нахождение общего решения методом характеристик
- А. науковий факт, b. гіпотеза, с. метод
- Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
- Агрегативна стійкість, коагуляція суспензій. Методи отримання.
- АгротехнІЧНИЙ метод
- Адаптовані й специфічні методи дослідження у журналістикознавстві
- Адміністративні (прямі) методи регулювання.
| <== попередня сторінка | | | наступна сторінка ==> |
| Способи утримання худоби | | | Момент пари сил |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |