• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Метод Стокса визначення коефіцієнта в’язкості рідини

Сила внутрішнього тертя виникає як під час руху рідини відносно твердого тіла, яке знаходиться в стані спокою, так і під час руху твердого тіла відносно рідини, яка знаходиться в стані спокою. Остання ситуація використовується при вимірюванні коефіцієнту в´язкості методом Стокса.

В´язкість рідини поряд з іншими чинниками (форма тіла, умови обтікання тощо) визначає силу опору, яка діє на тіло, що рухається в цій рідині.

На кульку, яка рухається у рідині, буде діяти сила опору, яка залежить від в´язкості рідини – η, радіусу кульки – r та швидкості її руху 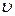. Вираз для сили опору середовища, в якому рухається кулька, вперше була отримана Стоксом і має такий вигляд:

. (4)

Важливим є те, що ця формула отримана за умови ламінарного обтікання кульки, тобто такого, при якому шари рідини можна вважати паралельними один одному. Такі умови практично виконуються при досить малих швидкостях руху кульки. Якщо ця умова не виконується, то в рідині утворюються турбулентності і тоді в´язкість, як властивість рідини, втрачає зміст. Для оцінки ламінарності існує спеціальний критерій – число Рейнольдса. За критичне значення числа Рейнольдса для руху кульки в рідині приймають Re_КР=10.

Метод Стокса для визначення в´язкості полягає у вимірюванні швидкості падіння кульки, яка встановилася сталою, в досліджуваній рідині.

Очевидно, що на кульку радіусу r (об´ємом 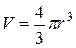), яка падає у в´язкому середовищі, діють такі сили (див. рис. 4):

сила тяжіння 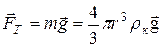;(5)

виштовхуюча сила Архімеда ; (6)

сила Стокса (сила опору рідини) 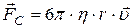. (7)

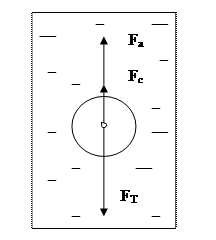
Рис.2. Сили, які діють на кульку, що падає в рідині.

Сила Стокса залежить від швидкості, тому вона буде зростати при падінні кульки, а отже, буде зростати і сила опору рідини. Цей ріст буде тривати доти, поки сила Стокса не зрівноважить суму сил тяжіння і Архімеда. У випадку такої рівноваги швидкість кульки припинить змінюватися і вона буде продовжувати рух з певною сталою швидкістю.

Отже, при усталеному русі кульки рівнодійна всіх сил, які діють на кульку, буде рівна нулю:

,

або за проекціями 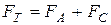. (8)

Використавши формули (5-7), співвідношення (8) перепишемо у вигляді:

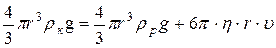. (9)

Розв´язавши (9) відносно η, отримаємо наступний вираз:

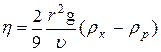. (10)

Використовуючи цю формулу, можна обчислити в´язкість рідини, якщо виміряна швидкість усталеного руху кульки.

Вираз (10) справедливий лише тоді, коли кулька падає в безмежному середовищі. Якщо кулька падає уздовж осі трубки радіуса r₀, то необхідно враховувати вплив бічних стінок. Виправлення у формулі Стокса для такого випадку теоретично обґрунтував Ладенбург. Формула для визначення коефіцієнта в'язкості з урахуванням виправлень приймає наступний вигляд:

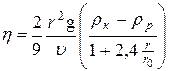. (11)

Читайте також:

1. A) Оцінка захисних споруд за ємністю – визначення коефіцієнта Квм.
2. B. Тип, структура, зміст уроку і методика його проведення.
3. CMM. Визначення моделі зрілості.
4. D) методу мозкового штурму.
5. Demo 11: Access Methods (методи доступу)
6. H) інноваційний менеджмент – це сукупність організаційно-економічних методів управління всіма стадіями інноваційного процесу.
7. I визначення впливу окремих факторів
8. I Метод Шеннона-Фано
9. I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
10. I. Метод єдиної подібності.
11. I. Метод рiвних вiдрiзкiв.
12. II. Визначення мети запровадження конкретної ВЕЗ з ураху­ванням її виду.

Переглядів: 7990