
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Тема 5: Визначення стійкості. Алгебраїчні критерії стійкості. Критерії стійкості Гурвіца і Рауса.
Теоретичні відомості
Під стійкістю системи автоматичного керування розуміютьїх здатність повертатись до вихідного усталеного режиму після короткочасної дії керуючої чи збурюючої величини, яка виводить систему з початкової рівноваги.
Динамічні властивості лінійних систем описуються неоднорідними диференційними рівняннями з постійними коефіцієнтами. Ці рівняння прийнято записувати у вигляді
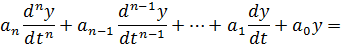
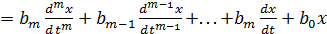 .
.
де y – регульована величина, x – вхідна дія.
Ліва частина диференціального рівняння описує вільний рух системи
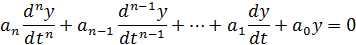
Цей рух стійкий, якщо
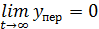
де 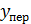 - загальний розв’язок однорідного диференціального рівняння.
- загальний розв’язок однорідного диференціального рівняння.
Розв’язок однорідного диференціального рівняння знаходять у формі
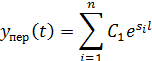
де  - сталі інтегрування,
- сталі інтегрування, 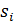 - корені характеристичного рівняння системи.
- корені характеристичного рівняння системи.
Характеристичне рівняння складається на основі диференціального рівняння системи. Разом з тим характеристичне рівняння є рівнянням для полюсів передаточної функції і може бути отримане з передаточної функції замкнутої системи, якщо знаменник передаточної функції прирівняти до нуля
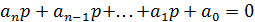 .
.
Корені характеристичного рівняння можуть бути дійсними або комплексними числами. Для довільних пари комплексних коренів можна записати 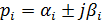
де 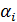 і
і  дійсна і уявна частини і кореня.
дійсна і уявна частини і кореня.
Для стійкості лінійних систем необхідно і достатньо, щоб корені характеристичного рівняння були від’ємними і комплексними числами від’ємними, дійсними частини. Загальну умову стійкості можна сформулювати інакше: система є стійкою коли корені характеристичного рівняння лежать в лівій півплощині комплексної площини коренів (рис. 7). Таким чином, уявна вісь є межею, яка ділить комплексну площину коренів на дві області – ліву стійку і праву – нестійку. Система знаходиться на межі стійкості, якщо один з коренів попадає на уявну вісь. При цьому в системі виникають автоколовання. В такому режимі лінійна система експлуатуватися не може.
jβ jβ
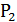

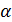 α
α
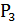
а) б)
Рис. 7 Аналіз стійкості за коренями характеристичного рівняння: а) – система стійка; б) – система нестійка.
Існують методи, що дозволяють досліджувати стійкість систем автоматичного керування без знаходження коренів характеристичного рівняння. Вони мають назву критеріїв стійкості. Критерії стійкості поділяються на алгебраїчні і частотні. До алгебраїчних належать критерії
Рауса, Гурвіна, Льєнара-Шіпара, до частотних – критерії Михайлова та Найквіста.
Найчастіше для аналізу стійкості систем невисокого порядку 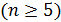 та систем, до складу яких не входять особливі ланки, використовують критерій Гурвіна, який приводить до тієї ж самої системи нерівностей, що і критерій Рауса. Тому, інколи, ці критерії називають критеріями Рауса-Гурвіна.
та систем, до складу яких не входять особливі ланки, використовують критерій Гурвіна, який приводить до тієї ж самої системи нерівностей, що і критерій Рауса. Тому, інколи, ці критерії називають критеріями Рауса-Гурвіна.
Для аналізу стійкості системиза критерієм Гурвіцаскладають визначник з коефіцієнтів характеристичного рівняння таким чином, що по головній діагоналі розташовують коефіцієнти від 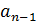 до
до 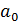 , далі місця в стовпцях над діагоналлю заповнюють коефіцієнтами в порядку зростання індексів, а знизу від діагоналі – із меншими індексами. Пусті місця заповнюють нулями.
, далі місця в стовпцях над діагоналлю заповнюють коефіцієнтами в порядку зростання індексів, а знизу від діагоналі – із меншими індексами. Пусті місця заповнюють нулями.
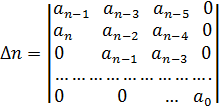
За критерієм Гурвіца замкнута система стійка, якщо при додатному знаку коефіцієнта 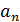 , є також додатним, головний визначник Гурвіца ∆ і всі його діагональні мінори -
, є також додатним, головний визначник Гурвіца ∆ і всі його діагональні мінори - 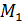 ,
, 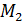 ,…,
,…, 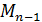 .
.
Діагональні мінори утворюють з головного визначника шляхом викреслювання відповідного числа рядків і стовпців.
Застосування критерію стійкості Гурвіца до системи першого і другого порядків показує, що вони є стійкими при додатних параметрах системи, однак системи третього і вищого порядків можуть втратити стійкість і при додатних значеннях параметрів.
Частотні критерії стійкості є досить зручними для аналізу стійкості систем високого порядку та систем із постійним запізненням.
При аналізі систем автоматичного керування важливо встановити аплив окремих параметрів системи на її стійкість та визначити область допустимих значень параметрів. Для цього можуть бути використані розглянуті вище критеріїстійкості метож D-розбиття.
Зокрема для знаходження критичного значення варійованого коефіцієнта передачі 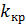 чи однієї з постійних часу
чи однієї з постійних часу 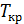 , при яких система буде знаходитись на межі області стійкості, можна скористатися критерієм стійкості Гурвіца. Для цього необхідно прирівняти до нуля головний визначник відповідні мінори визначника Гурвіца та розв’язати отримані рівняння. У випадку системи третього порядку (n=3) критичне значення параметру знаходять з розв’язку рівняння
, при яких система буде знаходитись на межі області стійкості, можна скористатися критерієм стійкості Гурвіца. Для цього необхідно прирівняти до нуля головний визначник відповідні мінори визначника Гурвіца та розв’язати отримані рівняння. У випадку системи третього порядку (n=3) критичне значення параметру знаходять з розв’язку рівняння
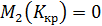
Задача №1. Проаналізувати стійкість САК. Система складається з регулятора інтегральної дії і об’єкта – двох послідовно з’єднаних аперіодичних ланок. Система замкнута.
X 
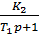
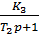 Y
Y
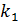 =2;
=2; 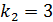 ;
; 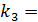 0,1;
0,1; 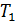 =0,5c;
=0,5c;  =0,2c.
=0,2c.
Знайдемо передаточну функцію розімкнутої системи.
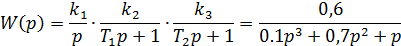
.
Передаточна функція замкнутої системи:
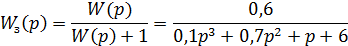
. Складаємо визначник Гурвіца:
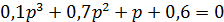 ;
;
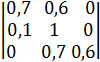
1. 0,7>0;
2. 0,64>0;
3. 0,83>;
4.  >0;
>0;
Отже система стійка.
Перевіряємо стійкість САК за критерієм Михайлова:
0,1 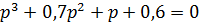 ;
;
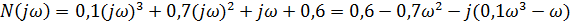 ;
;
 ;
;
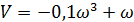 ;
;
По цим значенням будуємо таблицю.
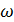 U V
U V
0 0,6 0
1 -0,1 0,9
2 -2,2 1,2
3 -5,7 2,1
4 -10,6 -2,4
∞ -∞ -∞
Для того щоб дізнатись чи є система стійкою, потрібно по даним цієї таблиці побцдцвати годограф, і пересвідчитись, що він проходить три квадранти.
Читайте також:
- A) Оцінка захисних споруд за ємністю – визначення коефіцієнта Квм.
- CMM. Визначення моделі зрілості.
- I визначення впливу окремих факторів
- II. Визначення мети запровадження конкретної ВЕЗ з урахуванням її виду.
- II. Мотивація навчальної діяльності. Визначення теми і мети уроку
- III. КРИТЕРІЇ ДОПУСКУ ДО СКЛАДАННЯ ПІДСУМКОВОГО МОДУЛЬНОГО КОНТРОЛЮ (ЕКЗАМЕНУ).
- Ocнoвнi визначення здоров'я
- S Визначення оптимального темпу роботи з урахуванням динаміки наростання втоми.
- V. ЗАХИСТ КУРСОВОЇ РОБОТИ ТА КРИТЕРІЇ ОЦІНЮВАННЯ
- V. КРИТЕРІЇ ОЦІНЮВАННЯ КУРСОВОЇ РОБОТИ
- VI. СИСТЕМА ТА КРИТЕРІЇ ОЦІНЮВАННЯ ЗНАНЬ СТУДЕНТІВ
- VІ. ЯКІСНІ КРИТЕРІЇ ОЦІНЮВАННЯ КУРСОВОЇ РОБОТИ
| <== попередня сторінка | | | наступна сторінка ==> |
| Тема 4: Амплітудні та фазові частотні характеристики елементарних ланок | | | Тема 6: Лінійна та квадратична інтегральні оцінки якості |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |