• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Розподіл напружень в ґрунтовому середовищі при різних умовах завантаження. Визначення тиску ґрунту від власної ваги та додаткового тиску в інженерній практиці.

В будь-якій точці грунтового масиву виникає система напружень, спричинена власною вагою вищележачих шарів грунту – природні напруження та прикладеного до поверхні грунтового масиву зовнішнього навантаження – додаткові напруження. Дослідженням встановлено: грунт в більшості випадків не є пружним тілом (залишкові деформації в грунті значно більші від пружних – компресійна крива рис. 4.2); грунту не властива строга лінійна залежність між напруженнями і деформаціями (компресійна крива рис. 4.2). Крім того, в більшості випадків грунт є несуцільним (дисперсним) тілом (п. 1.2). В зв‘язку з цим виникає питання, в яких випадках допустимо використовувати рішення теорії пружності, для визначення напружень в грунтах. Для вияснення цього розглянемо переміщення фундамента від дії статичного навантаження.

Напруження в грунті від дії зосередженого навантаження. Напружений стан у деякій точці простору характеризується сукупністю діючих у ній напружень. В умовах просторової задачі виділяють такі напруження (рис. 7.3).

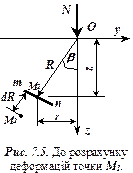
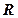Полярні координати і 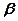. Переміщення точки 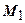у напрямку радіуса (окрім зони біля точки прикладення сили ) буде

, де (7.1)

- коефіцієнт пропорційності.

Розглянемо зараз точку , розміщену на продовженні радіуса 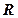на відстані 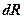від точки 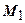. Керуючись записаним виразом (7.1), переміщення точки у напрямку радіуса 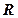становитиме

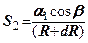
Відносна деформація грунту на відрізку 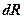буде

(7.3)

Нехтуючи величиною 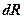(незрівнянно малою у порівнянні з 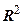) маємо

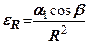(7.4)

Згідно з законом Гука, залежність між напруженнями і деформаціями має вигляд 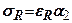( 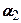- коефіцієнт пропорційності між напруженнями і деформаціями). Підставивши сюда вираз (7.3) знайдемо залежність для напружень стиснення 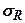, які діють на ділянки, перпендикулярні напрямку радіуса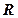

(7.5)

Для знаходження добутку коефіцієнтів 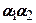виріжемо умовно частину напівпростору напів-шаровою поверхнею (рис. 7.6), яка має центр в точці і радіус 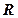, і складемо рівняння рівноваги проекцій на вісь 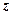всіх сил, які діють на вирізаний елемент. Отримаємо

Перейдемо до декартової системи координат. Оскільки 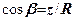(рис. 7.5), то

(7.9)

Врахувавши те, що 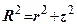і підставляємо його у вираз (7.9), матимемо

Позначимо - табличний коефіцієнт, тоді

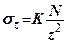(7.11)

Аналогічним чином можуть бути знайдені решта напружень .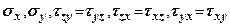

Якщо на поверхні діє декілька сил (рис.7.8), то

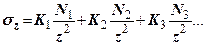(7.12)

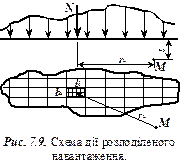Напруження в грунті від дії розподіленого навантаження. Нехай до поверхні лінійно-деформованого напівпростору в мажах площі 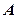прикладено розподілене навантаження змінної в плані інтенсивності (рис. 7.9). Завантажену площу можна розбити на невеличкі прямокутники із сторонами 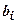, 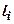і більш складні фігури в межах контуру площі 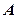. З деяким наближенням тиск, який розподілено в межах і-го прямокутника можна замінити рівнодіючою , прикладеною в центрі ваги цього тиску. Вертикальне стискуюче напруження в будь-якій точці напівпростору від зосередженої сили можна знайти по аналогії з виразом (7.11)

Визначивши величину 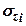від навантаження кожної з елементарних фігур, на які розбита площа 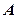і провівши сумування цих напружень, визначимо сумарне напруження

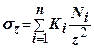(7.13)

Напруження в грунті від дії розподіленого навантаження по смузі. У попередньому пункті (п. 7.5) ми розглянули задачу, коли напруження змінюються у всіх трьох напрямках осей координат. Якщо навантаження розподілене по нескінченній смузі і величина його вздовж смуги не змінюється (рис. 7.11), то для оцінки напружено-деформованого стану масиву достатньо дослідити розподіл напружень у будь-якому поперечному перерізі масиву. Така задача має назву "плоскої". Щодо практичних випадків, то будь-яка задача може бути розглянута як плоска, якщо довжина фундаменту в 10 разів і більше перевищує його ширину.

Вирази для складових напружень при дії рівномірно розподіленого навантаження мають вигляд

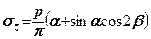(7.18)

(7.19)

, де (7.20)

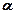- кут зору (рис. 7.11).

З (7.20) видно, що дотичні напруження відсутні, коли кут 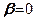, тобто коли нормаль ділянки 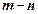співпадає з бісектрисою кута зору (під центром фундаменту). На цих ділянках діють більші головні напруження 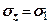, на перпендикулярних - менші 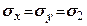(рис. 7.11). Ці напруження визначають за формулами

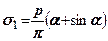(7.21)

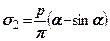(7.22)

Напруження в грунті від його власної ваги (природні). На деякій глибині 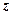від поверхні нормальні напруження 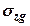від власної ваги грунту на ділянках, паралельних поверхні грунту, становитимуть (рис. 7.12)

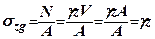, де

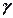- питома вага грунту; 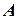- площа поперечного перерізу виділеної призми.

В тому випадку, коли питома вага змінюється з глибиною, товщу грунту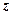

ділять на окремі шари товщиною

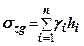, де

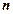- число шарів грунту; , - питома вага і товщина кожного шару: .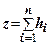

Нормальні бічні напруження 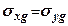(бічний тиск грунту у стані спокою) визначають за формулою

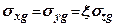, де

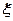- коефіцієнт бічного тиску грунту.

У шарах, розташованих нижче рівня грунтових вод, питома вага всіх водопроникних грунтів приймається з урахуванням зважуючої дії води

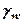, де - питома вага води.

При наявності водонепроникного шару (глина, важкі суглинки) на рівні його поверхні епюра матиме горизонтальну ділянку, яка дорівнюватиме

, де 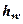- товщина шару води.

Читайте також:

1. A) Оцінка захисних споруд за ємністю – визначення коефіцієнта Квм.
2. CMM. Визначення моделі зрілості.
3. H.2 ВИСЯЧІ ЗАБИВНІ ПАЛІ ВСІХ ВИДІВ І ПАЛІ-ОБОЛОНКИ, ЩО ЗАНУРЮЮТЬ БЕЗ ВИЙМАННЯ ҐРУНТУ
4. I визначення впливу окремих факторів
5. I. Доповнення до параграфу про точкову оцінку параметрів розподілу
6. II. Визначення мети запровадження конкретної ВЕЗ з ураху­ванням її виду.
7. II. Мотивація навчальної діяльності. Визначення теми і мети уроку
8. IV. НС у природному середовищі та інших сферах життєдіяльності людини
9. IV. Розподіл нервової системи
10. O ексклюзивний розподіл на правах винятковості.
11. Ocнoвнi визначення здоров'я
12. S Визначення оптимального темпу роботи з урахуванням динаміки наростання втоми.

Переглядів: 3042