• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Визначення

Множини. Способи задания множин

Елементи множини, способи задания множин, скінченні та нескінченні множини, упорядковані множини, парадокси

В повсякденному житті та практичній діяльності часто доводиться говорити про деякі сукупності різних об'єктів: предметів, понять, чисел, символів тощо. Наприклад, сукупність деталей механізму, аксіом геометрії, чисел натурального ряду, літер абетки. На основі інтуїтивних уявлень про подібні сукупності сформувалося математичне поняття множини. Значний внесок до теорії множин зробив Георг Кантор. Згодом завдяки його дослідженням теорія множин стала цілком визначеною та обґрунтованою галуззю математики, а на сьогодні вона здобула фундаментального значення. Теорія множин є підставою для всіх розділів дискретної математики та комп'ютерних наук в цілому, є однією з основ функціонального аналізу, топології, загальної алгебри. Глибокі дослідження в самій теорії множин пов'язані з основами математики.

Теорія множин разом з іншими розділами дискретної математики має безліч корисних застосувань у програмуванні. Вона використовується для побудови систем управління базами даних, під час побудови та організації роботи комп'ютерних мереж, зокрема мережі Інтернет.

Множина є настільки загальним і водночас початковим поняттям, що її строге визначення через більш прості поняття дати важко. Тому вслід за Г. Кантором ми приймаємо інтуїтивне уявлення про множину як сукупність деяких елементів, цілком визначених у випадку кожної конкретної множини.

Множини позначають великими, а елементи множин — малими латинськими буквами або малими латинськими буквами з індексами. Елементи множин часто відокремлюються фігурними дужками. Наприклад, запис А={а, b, d, h} означає, що множина А складається з чотирьох елементів а, b, d, h. В загальному вигляді твердження, що скінчена множина А складається з п елементів, записується так: А = {а₁, а₂, ..., а_n}.Належність елемента множині позначається символом Î: а Î А (читають: елемент а належить множині А). В протилежному випадку позначають аÏ А (читають: елемент ане належить множині А).

Далі використовуються такі загальноприйняті позначення основних числових множин.

N— множина натуральних чисел, N = {1, 2, 3 ...}.

Z— множина цілих чисел, Z ={..., -3 -2, -1, 0, 1,2,3,...}.

Q— множина раціональних чисел. Будь-яке раціональне число можна зобразити у вигляді дробу: а/b де а, b Î Z,b¹ 0.

R— множина дійсних чисел. Будь-яке дійсне число можна зобразити у вигляді нескінченного десяткового дробу a, b₁b₂b₃ ... b_n ... із цілою частиною а Î Z і b_k Î {0, ..., 9}. Множині дійсних чисел відповідає множина точок на числовій прямій.

Елементами множин можуть бути інші множини, тоді ці елементи позначатимуться великими буквами.

Приклад.А = {D, С}, D = {a, b}, C = {c, d, e}. При цьому D Î А, С Î А, але a Ï А і с Ï А.

Приклад.Е = {{1, 2}, 3}. Цей запис означає, що множина Е містить два елементи: множину {1, 2} і елемент 3.

Множина називається скінченною, якщо вона містить скінченне число елементів, і нескінченною,якщо вона містить необмежене число елементів.

Приклад.Множина А = {1, 2, 3, 4, 5, 6, 7, 8, 9, 0} цифр в десятковій системі числення скінченна, а множина точок кола нескінченна.

Упорядкованоювважається така множина, в якій важливі не тільки її елементи, але і порядок їх наступності у множині. Наприклад, упорядкованою є множина, в якій кожний елемент має свій порядковий номер. Позначають упорядковану множину, як правило, або круглими, або трикутними дужками. Наприклад,

А=<1, 2, 3>,

А = <а₁ а₂, ..., а_n >, п Î N;

В = (а, b, с).

Приклад.Розглянемо упорядковану множину А = (х, у)географічних координат довготи х та широти у. Якщо довготу і широту поміняти місцями, в результаті можна потрапити віншу точку всесвіту.

Вказати порядковий номер для всякого дійсного числа на множині R неможливо, і порядок у R задається за допомогою порівнянь < і £. Тому загальне визначення упорядкованої множини X припускає, що для всіх пар елементів зX визначено відношення порядку (див. п. 2.4)

Способи задания множин

1. Множину можна задати простим переліком елементів

А = {а₁, а₂, ..., а_n}.

Приклад.Множину відмінників у групі позначимо O і задамо її переліком: О = {Іванов, Петров, Сидоров, Кукушкіна}.

Спосіб задания множини переліком її елементів не придатний для задания нескінченних множин, а у випадку скінченних множин його практично часто не можна реалізувати. Так, не можна перелічити множину риб у Тихому океані, хоча їхнє число скінченне.

2. Інший спосіб задания множини складається з опису елементів визначеною властивістю: X = {х | Р(х)},де Р(х)означає, що елемент х має властивість Р(х).

Приклад.Множину N₁₀всіх натуральних чисел, менших за 10, можна задати так: N₁₀ = {x | х Î N, х < 10}.

Властивості елементів можуть бути задані не формально, а за допомогою опису на природній мові.

Приклад.Множина S студентів групи ПМ-04-1, які одержують стипендію.

Приклад.У геометрії часто доводиться мати справу з множинами, що задані своїми характеристичними властивостями. Так, коло — геометричне місце точок площини, що рівновіддалені від центра даної точки цієї площини.

3. Множина може бути задана рекурсивно вказівкою способу послідовного породження її елементів.

Приклад.Множина значень рекурсивної функції є рекурсивно-заданою множиною , де ф, є 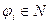, і=1,2,3,.... Нехай φ₁ = 1, φ₂ = 2, а кожне наступне число залежить від двох попередніх таким чином:

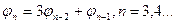
Тоді

;

і т. д.

При заданні множин можуть виникати помилки та протиріччя. Множина задана коректно, якщо для будь-якого елемента можна визначити, належить він множині чи ні.

Приклад.Визначення множини А як множини, що містить будь-які п'ять натуральних чисел, не є коректним, оскільки неможливо визначити точно елементи А. Множина всіх простих чисел визначена коректно. Для будь-якого натурального числа можна перевірити, чи є воно простим, хоча практично на це може знадобитися дуже багато часу.

Приклад.Множина всіх динозаврів, що жили на Землі, є множиною, що задана правильно. Хоча практично неможливо визначити елементи цієї множини, але теоретично ясно, що якщо тварина, яка будь-коли жила на Землі, є динозавром, то вона належить до цієї множини, у протилежному випадку — ні.

Некоректність задания множини часто пов'язана з протиріччям при перевірці належності деякого елемента множині. Наведемо два класичних приклади.

Приклад.Визначимо множину G як множину всіх множин, які не є елементами самих себе. Але тоді не можна з'ясувати, чи є сама множина G елементом множини G. Якщо так, то приходимо до протиріччя, оскільки G містить як елементи тільки множини, які не є елементами самих себе. Якщо множина G не є елементом самої себе, то тоді, за визначенням, вона повинна бути елементом множини G, що є протиріччям.

Приклад.Єдиний перукар у місті N визначає множину К мешканців, яких він повинен голити, як сукупність всіх тих мешканців N, які не голяться самі. Але тоді для самого перукаря виходить протиріччя і при включенні його до множини К, і при віднесенні його до мешканців, які голяться самі.

Такі протиріччя називаються логічними парадоксами і вивчаються в математичній логіці.

Читайте також:

1. I визначення впливу окремих факторів
2. II. Визначення мети запровадження конкретної ВЕЗ з ураху­ванням її виду.
3. II. Мотивація навчальної діяльності. Визначення теми і мети уроку
4. Ocнoвнi визначення здоров'я
5. Алгебраїчний спосіб визначення точки беззбитковості
6. Аналіз службового призначення деталей та конструктивних елементів обладнання харчових виробництві, визначення технічних вимог і норм точності при їх виготовленні
7. Аналіз стратегічних альтернатив та визначення оптимальної стратегії формування фінансових ресурсів
8. Аналіз ступеня вільності механізму. Наведемо визначення механізму, враховуючи нові поняття.
9. Балансова теорія визначення статі. Диференціація статі і роль гормонів у цьому процесі.
10. Безстатеве розмноження, його визначення та загальна характеристика. Спори — клітини безстатевого розмноження, способи утворення і типи спор.
11. Біостратиграфічні методи визначення віку порід
12. Біуретовий метод визначення білків

Переглядів: 776