Визначення

Визначення

Взаємно однозначною називається така відповідністьміж множинами А і В, при якій кожному елементу а Î А відповідає один і тільки один елемент b Î В, і кожному елементу b Î В відповідає один і тільки один елемент а Î А. Функція, що визначає взаємно однозначну відповідність, називається бієктивною функцією або бієкцією.

Множини А і В називаються еквівалентнимиабо рівно-потужними(А ~ В),якщо між ними можна встановити взаємно однозначну відповідність.

У прикладі із заповненим залом для глядачів множина глядачів еквівалентна множині крісел. Таким чином, еквівалентними одна одній виявляються всі скінченні множини з однаковим числом елементів п,і число п вважається потужністюцих множин.

Для нескінченної множини строге поняття потужності не вводиться, але сам термін «потужність»використовується для позначення властивості, загальної для всіх еквівалентних множин. Якщо дві нескінченні множини А і В еквівалентні (А ~ В),то рівність їх потужностей формально записується як |А| = |В|.
Множина А називається зчисленною,якщо вона еквівалентна натуральному ряду N (А ~ N). Термін «зчисленність»є точним замінником інтуїтивного поняття — «дискретність».

За допомогою бієкції φ = N → А можна «перелічити» всі елементи а з А,привласнивши їм індекси за правилом φ(n) = а_п. Можна записати, що А = {а_п, п=1, 2, ...}. Множини парних натуральних чисел N₄ = {2, 4, ..., т, ...}, всіх натуральних чисел N = {1, 2, ..., п, ...}, цілих чисел Z і раціональних чисел Q послідовно вкладені: N_чÌ N Ì Z Ì Q. Хоча для будь-яких двох з цих множин немає рівності, вони еквівалентні одна одній,тобто мають однакову потужність і є зчисленними: |N_ч| = |N| = |Z| = |Q|. Тому відповідно до наших угод множини N_ч, N, Z, Q є дискретними.

Дійсно, еквівалентність N ~ N_чаргументується за допомогою бієкції φ(n) = 2п : 2п = т. Множину цілих чисел Z можна «перелічити» (тобто присвоїти його елементам натуральні індекси) за правилом:

m n …

1/1 2/1 3/1 4/1 …

1/2 2/2 3/2 4/2 …

1/3 2/3 3/3 4/3 …

1/4 2/4 3/4 4/4 …

… … … … … …

Рис. 1.14. Таблиця множини Q₊

0 = z₁; 1 = z₂; -1 = z₃;

2 = z₄; -2 = z₅; 3 = z_6;…

Отже Z ~ N.

Для доведення еквівалентності множин Q і N достатньо вказати правило нумерації множини Q₊ додатних раціональних чисел, що утворяться діленням т/п натуральних чисел т і п.

Пронумеруємо стовпці та рядки нескінченної таблиці індексами т і п відповідно (рис. 1.14).

Будемо нумерувати послідовно числа п/т вздовж пунктирних похилих стрілок, починаючи з лівого верхнього кута таблиці і переходячи після проходження кожної стрілки до сусідньої, більш довгої. При цьому пропускаються відношення т/п, чисельні значення яких зустрічалися раніше:

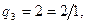
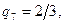
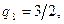
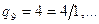
Таким чином, множина Q раціональних чисел зчисленна:

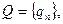
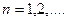
Звичайно, існують нескінченні незчисленнімножини, та їх потужність природно вважати більшою за |N|. Так, множина точок відрізка [0, 1] = {х Î R;0 £ х £1} не є зчисленною (теорема Г. Кантора). її потужність називається континуумі позначається малою буквою с: |[0, 1]| = с. Сама множина [0, 1] і будь-яка еквівалентна їй множина називаються континуальними.

Виявляється, що на дійсній вісі R континуальними (тобто еквівалентними одна одній і відрізку [0, 1]) є, наприклад, множини [а, b], (а, b),при будь-якому а < b; (0, +¥); множина (- ¥, +¥), що дорівнює R.

Континуальні також множини точок будь-якого квадрату та кругу на площині R², паралелепіпеду та кулі у просторі R³і самого простору R³: |R| = |R²| = |R³| = с.
Читайте також:
I визначення впливу окремих факторів
II. Визначення мети запровадження конкретної ВЕЗ з урахуванням її виду.
II. Мотивація навчальної діяльності. Визначення теми і мети уроку
Ocнoвнi визначення здоров'я
Алгебраїчний спосіб визначення точки беззбитковості
Аналіз службового призначення деталей та конструктивних елементів обладнання харчових виробництві, визначення технічних вимог і норм точності при їх виготовленні
Аналіз стратегічних альтернатив та визначення оптимальної стратегії формування фінансових ресурсів
Аналіз ступеня вільності механізму. Наведемо визначення механізму, враховуючи нові поняття.
Балансова теорія визначення статі. Диференціація статі і роль гормонів у цьому процесі.
Безстатеве розмноження, його визначення та загальна характеристика. Спори — клітини безстатевого розмноження, способи утворення і типи спор.
Біостратиграфічні методи визначення віку порід
Біуретовий метод визначення білків

Переглядів: 512

<== попередня сторінка | наступна сторінка ==>

Завдання | Основні типи фізичних кабінетів

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.006 сек.