• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Властивості функції розподілу

Властивість 1. Значення функції розподілу належать відрізку [0, 1]:

.

Доведення. Властивість витікає з визначення функції розподілу як ймовірності: ймовірність завжди є невід’ємне число, що не перевищує одиниці.

Властивість 2. F(х) - не спадна функція, тобто

, якщо .

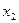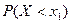Доведення. Хай . Подію, що полягає в тому, що Х прийме значення, менше , можна підрозділити на наступні дві несумісні події: 1) Х прийме значення, менше , з імовірністю ; 2) Х прийме значення, що задовольняє нерівність , з імовірністю . За теоремою додавання маємо

.

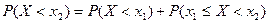Звідси

.

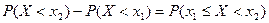або

. (*)

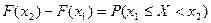Оскільки. будь-яка ймовірність є число невід’ємне, т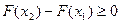о , або , що і вимагалося довести.

Наслідок 1. Імовірність того, що випадкова величина прийме значення, укладене в інтервалі (а, b), рівна приросту функції розподілу на цьому інтервалі:

. (**)

Цей важливий наслідок витікає з формули (*), якщо покласти x₁=a і х₂=b.

Наслідок 2. Імовірність того, що безперервна випадкова величина Х прийме одне певне значення, рівна нулю.

Дійсно, поклавши у формулі (**) а=x₁, b=x₁+Dx, маємо

.

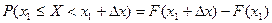Спрямуємо Dx до нуля. Оскільки Х - безперервна випадкова величина, то функція F(х) безперервна. Через неперервність F(х) в точці х₁ різниця 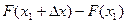також прагне до нуля; отже, Р (Х=х₁)=0. Використовуючи це положення, легко переконатися в справедливі рівностей

. (***)

Наприклад, рівність доводиться так: .

Таким чином, не представляє інтересу говорити про імовірність того, що безперервна випадкова величина прийме одне певне значення, але має сенс розглядати імовірність попадання її до інтервалу, хай навіть скільки завгодно малого. Цей факт повністю відповідає вимогам практичних задач. Наприклад, цікавляться імовірністю того, що розміри деталей не виходять за дозволені границі, але не ставлять питання імовірності їх співпадіння з проектним розміром.

Відмітимо, що було б неправильним думати, що рівність нулю імовірності Р(Х=х₁) означає, що подія Х=x_l неможлива (якщо, звичайно, не обмежуватися класичним визначенням імовірності). Дійсно, результаті випробування випадкова величина обов’язково прийме одне з можливих значень; зокрема, це значення може виявитися рівним х₁.

Властивість 3. Якщо можливі значення випадкової величини належать інтервалу (а, b), то: 1) F(x)=0 при 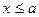; 2) F(x)=l при .

Доведення. 1) Хай . Тоді подія Х<х₁ неможлива (оскільки значень, менших х₁, величина Х за умовою не приймає) і, отже, імовірність її рівна нулю.

2) Хай . Тоді подія Х<x₂ достовірна (оскільки всі можливі значення Х менші х₂) і, отже, імовірність її рівна одиниці. Г

Наслідок. Якщо можливі значення безперервної випадкової величини розташовані на всій осі х, та справедливі наступні граничні співвідношення:

; .

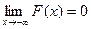Читайте також:

1. I. Доповнення до параграфу про точкову оцінку параметрів розподілу
2. Авоматизація водорозподілу регулювання за нижнім б'єфом з обмеженням рівнів верхнього б'єфі
3. Автоматизація водорозподілу з комбінованим регулюванням
4. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
5. Автоматизація водорозподілу регулювання зі сталими перепадами
6. Автоматизація водорозподілу регулюванням з перетікаючими об’ємами
7. Автоматизація водорозподілу регулюванням за верхнім б'єфом
8. Автоматизація водорозподілу регулюванням за нижнім б'єфом
9. Адвокатура в Україні: основні завдання і функції
10. Аеродинамічні властивості колісної машини
11. Алгоритм знаходження ДДНФ (ДКНФ) для даної булевої функції
12. Але відмінні від значення функції в точці або значення не існує, то точка називається точкою усувного розриву функції .

Переглядів: 1189