• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Рівняння поверхні та лінії в просторі

Рівнянням поверхні в заданій системі координат 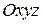називається таке рівняння з трьома змінними, якому задовольняють координати довільної точки поверхні і не задовольняють координати точок, що не лежать на ній.

Координати , і довільної точки, що входять в рівняння поверхні, називаються поточними координатами.

Приклад 7.3.Скласти рівняння сфери радіуса з центром в початку координат.

Розв’язок. Як відомо, сфера – це множина точок простору, рівновіддалених від даної точки, яку називають центром. Візьмемо на сфері довільну точку . Відстань від цієї точки до центра кола рівна , тобто або . Отриманому рівнянню задовольняють координати довільної точки сфери і не задовольняють координати точок, що не лежать на ній, так як для точок, що лежать всередині сфери, 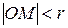, а для точок, що лежать зовні – . t

Приклад 7.4.Скласти рівняння координатної площини .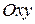

Розв’язок. Рівнянню 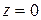задовольняють координати довільної точки площини 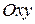і не задовольняють координати точок, що не лежать на ній. t

Лінія в просторі задається як лінія перетину двох поверхонь.

Нехай дано рівняння поверхонь , , 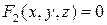які перетинають по лінії .

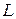Систему рівнянь

якій задовольняють координати довільної точки лінії 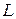і не задовольняють координати точок, що не лежать на ній, називають рівняннями лінії в просторі.

Приклад 7.5.В системі координат 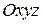скласти рівняння кола, що лежить в площині 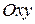, радіуса з центром в початку координат.

Розв’язок. Дане коло можна розглядати як лінію перетину площини 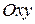і сфери радіуса з центром в початку координат:

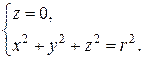t

Теоретичні питання

7.1. Що називається рівнянням лінії на площині?

7.2. Що називається рівнянням поверхні?

7.3. Що називається рівняннями лінії в просторі?

Задачі та вправи

7.1. Скласти рівняння множини точок площини, рівновіддалених від точок і .

7.2. Вияснити, які з точок , , 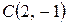лежать на колі .

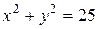7.3. Лінії задані рівняннями: а) 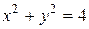; б) ;

в) ; г) .

Вияснити, які з них проходять через початок координат.

7.4. Скласти рівняння сфери радіуса з центром в точці .

7.5. Скласти рівняння сфери з центром в точці 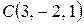, що проходить через точку .

Читайте також:

1. V Процес інтеріоризації забезпечують механізми ідентифікації, відчуження та порівняння.
2. Алгоритм розрахунку температури поверхні чипу ІМС процесора
3. Анатомія параректальних просторів
4. Асимптотичний підхід до порівняння оцінок
5. Білінійні і квадратичні форми в евклідовому просторі
6. Бюджетний контроль - це порівняння показників бюджету зі звітом за від­повідний період часу.
7. Бюджетні множини й лінії бюджетного обмеження
8. В обох випадках основним розрахунковим рівнянням є рівняння теплопередачі і теплового балансу
9. В українському інформаційному просторі аналітична журналістика також повинна відіграти вже зараз видатну роль: збудувати духовну будівлю українського національного світу.
10. Вивід основного рівняння фільтрації
11. Визначення довжини лінії
12. Визначення температури на поверхні ізоляції принадземномупрокладанні та при прокладанні трубопроводів в приміщенні.

Переглядів: 1489