• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Позначення та приклади

РВВ ДНУ

А.В. Тушев

„ЕЛЕМЕНТИ ЗАГАЛЬНОЇ ТОПОЛОГІЇ”

(Опорний конспект лекцій)

Дніпропетровськ

ЗМІСТ

ЗМІСТ

1. Метричні простори.

2. Відкриті множини метричних просторів та їх властивості.

3. Топологія. Топологічні простори. Приклади.

4. Замкнені підмножини топологічного простору.

5. Внутрішні точки. Внутрішність підмножини топологічного простору.

6. Точки дотику. Замикання підмножин топологічного простору.

7. Ізольовані, граничні, межові точки.

8. База топологічного простору. Введення топології за допомогою бази .

9. Неперервне відображення топологічних просторів. Гомеоморфізми.

10. Компактні топологічні простори.

Список використаної літератури.

§1. Метричні простори.

Нехай М – множина. Метрикою, заданою на М, називається закон (правило), який кожній упорядкованій парі елементів із М (М) ставить у відповідність деяке дійсне, невід’ємне число , причому так, що виконуються наступні аксіоми:

М1. Аксіома тотожності:

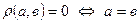
М2. Аксіома симетричності:

М3. Аксіома трикутника:

Таким чином, метрика 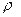на М – це відображення 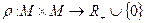, яке задовольняє аксіомам М1 – М3.

Якщо на М задана метрика , то пару 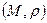називають метричним простором з метрикою .

Елементи простору М називають його точками, а величину - відстанню між точками а і в.

Зазначимо, що поняття метрики узагальнює поняття відстані з Евклідової геометрії, оскільки ця відстань задовольняє означенню метрики.

Приклади:

1. На множині R введемо метрику за правилом: =|a - в|.

Аксіоми М1, М2 – очевидні. А оскільки

,

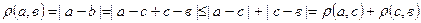то отримали аксіому М3. Таку метрику називають природною.

1. Дискретна метрика.

Нехай М – довільна множина, введемо на М метрику наступним чином:

Аксіоми М1, М2 – очевидні з означення цієї метрики. 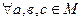розглянемо усі можливі значення метрик із співвідношення:

(*)

Якщо =0, то співвідношення (*) виконується незалежно від значень метрик у його правій частині. Якщо ж =1, то

Таким чином, - метрика на М, яку називаютьдискретною метрикою на М.

1. Нехай Е – п-вимірний Евклідовий простір, тобто Е – п-вимірний векторний простір над полем R, на якому введений скалярний добуток (<a,в>). За допомогою скалярного добутку вводиться довжина вектору евклідового простору

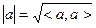
4. 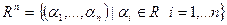- множина усіх можливих рядків довжини п з дійсними коефіцієнтами 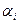. Відомо, що - векторний простір над полем R.

Якщо операцію додавання і зовнішнього множення ввести по-координатно, крім того є векторним простором і скалярний добуток ввести за формулою:

Тоді згідно приклада 3: - метричний простір, на якому метрика задається за формулою:

(1)

Метрику на , введену за формулою (1), називають Евклідовою.

5. Окрім Евклідової метрики, що була введена на за формулою (1), на цій множині можна ввести й інші метрики:

Перевіримо аксіоми метрики для :

М1: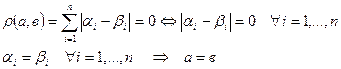

М2:

М3:

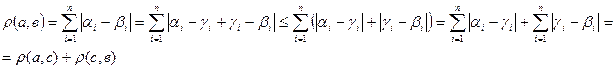Крім того, на можна ввести ще метрику 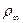за формулою:

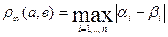
М1:

М2:

М3: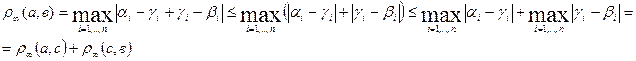

Таким чином, на одній і тій же множині М, у загальному випадку, можна ввести багато метрик, тому позначення метрик у позначенні метричного простору відіграє суттєву роль: різні метричні простори. Але якщо заздалегідь відомо, про яку метрику йде мова, то метричний простір можна позначити лише символом, що позначає множину, на якій задана метрика.

6. Нехай - множина неперервних на відрізку функцій.

На цій множині можна ввести метрики, наприклад за формулою

.

Але на можна ввести й інші метрики, наприклад за такою формулою:

§2. Відкриті множини метричних просторів та їх властивості

Нехай 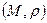- метричний простір, 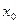- елемент простору, .

Множина 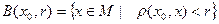називається відкритою кулею з центром у точці 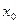і радіусом .

Множина називається замкненою кулею з центром у точці 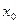і радіусом .

Множина 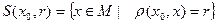називається сферою з центром 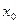і радіусом .

Множину називають 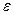-околом точки .

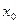В метричному просторі можна ввести означення відстані між його підмножинами,а саме, якщо , то .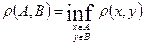

Означення відстані між підмножинами дозволяє ввести означення 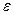-околу підмножини А метричного простору. А саме, якщо 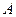міститься в М, то

Нехай М - метричний простір, U – підпростір простору М, називають відкритою множиною, якщо або U – пуста множина, або будь-яка точка з U входить в U разом з деяким своїм 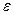-околом. Тобто

Твердження 1:Нехай М – метричний простір, , тоді:

1. Відкрита куля - відкрита множина.
2. - відкрита множина.

Теорема 2 (властивості відкритих множин метричного простору):

Нехай М – метричний простір, тоді сукупність усіх відкритих множин простору М задовольняє наступним властивостям:

1. Пуста підмножина та вся множина М є відкритими.
2. Об’єднання будь-якої кількості відкритих підмножин простору М є множиною відкритою.
3. Перетин будь-якої скінченної сукупності відкритих підмножин з М – відкрита множина в М.

Зауваження: Перетин нескінченної сукупності відкритих підмножин метричного простору може бути відкритим.

Розглянемо відкриті підмножини:

не є відкритою підмножиною, оскільки ніякий окіл числа 1 не попадає в множину (0,1].

Твердження 2: Підмножина U множини М є відкритою тоді і тільки тоді, коли U є об’єднанням деякої сукупності відкритих куль з М.

§3. Топологія. Топологічні простори. Приклади

Нехай Т – деяка множина, тоді булеан - сукупність усіх підмножин.

Деяка сукупність підмножин множини називається топологією на множині Т, якщо задовольняє наступним аксіомам (аксіомам топології)

Т1: пуста множина, сама множина Т містяться в .

Т2:

Об’єднання будь-якої сукупності підмножин з також належить до .

Т3:

Перетин скінченної сукупності підмножин з належить до .

Якщо на множині Т задана деяка топологія , то пару (Т, ) називають топологічним простором. При цьому елементи множини Т називаються точкамицього простору. А підмножини з називаються відкритими підмножинами з цього простору.

Якщо заздалегідь невідомо, про яку топологію на Т йде мова, то для позначення топологічного простору можна використовувати лише позначення множини Т.

Приклад 1: (М, ) – деякий метричний простір.

Нехай - сукупність всіх відкритих підмножин цього простору. За теоремою задовольняє всім аксіомам топології, тоді (М, ) є топологічним простором. Цю топологію називають топологією на М, індукованою метрикою , і позначається .

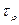Таким чином, поняття топологічного простору є деяким узагальненням метричного простору.

Нехай (Т, ) – деякий топологічний простір. Якщо на множині Т можна задати метрику , так що (Т, )=(Т, ), то кажуть, що топологія є метризованою.

Зазначимо, що далеко не всі топології є метризованими.

Приклад 2: Нехай Т – множина. =, тоді - топологія на Т, яку називають дискретною. Зазначимо, що дискретна топологія індукована дискретною метрикою. У цій топології усі підмножини з Т є відкритими. І зокрема, точки дискретного простору є відкритими підмножинами.

Приклад 3: Нехай Т – множина. 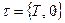, задовольняє всім аксіомам топології. Цю топологію називають тривіальною топологією на Т.

Приклад 4: Нехай Т – нескінченна множина, покладемо:

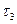є топологією на Т, яку називають топологією скінченних доповнень (топологією Заріського).

Приклад 5: Нехай (Т, ) – топологічний простір і нехай

Покажемо, що є топологією на множині А.

Таким чином, - топологія на підмножині А, яку називають топологією, індукованою на А топологією 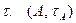називають підгрупою простору .

Таким чином, всяку підмножину простору Т можна розглядати як його підпростір з індукованою топологією.

Якщо , то 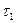- слабкіша, 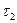- сильніша. Найслабкіша – тривіальна 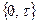, найсильніша – дискретна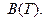

§4. Замкнені підмножини топологічного простору

- топологічний простір, називається замкненою, якщо 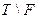- відкрита множина.

Приклад 1:

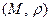- метричний простір, як було доведено раніше і - відкриті множини, тому множини 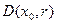та 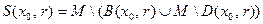є множинами замкненими

.

Приклад 2:

У дискретній топології замкненими будуть усі підмножини, оскільки в ній всі підмножини відкриті.

Приклад 3:

У топології скінченних доповнень, задані на нескінченній множині Т (топології Заріського) замкненими будуть 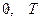та усі скінченні підмножини з Т.

Теорема 1 (властивості замкнених підмножин):

Нехай - топологічний простір. 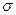-сукупність усіх замкнених підмножин цього простору, тоді 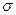має наступні властивості:

1.

2. Перетин будь-якої сукупності замкнених підмножин з Т є підмножина замкнена.

3. Об’єднання будь-якої скінченної сукупності замкнених підмножин з Т є підмножина замкнена.

підмножиною, оскільки її доповнення не є відкритою.

Теорема 2 (про введення топології за допомогою системи замкнених підмножин):

Нехай Т – деяка множина, 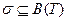, що задовольняє вимогам (1)-(3) попередньої теореми, тоді на множині Т існує топологія , для якої 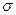є системою замкнених підмножин.

§5. Внутрішні точки.

Внутрішність підмножини топологічного

Читайте також:

1. В чому полягає явище тунелювання через потенціальний бар’єр, наведіть приклади.
2. Визначення і приклади
3. Графічне позначення матеріалу в перерізах і на виді - штрихування, що виконується тонкими суцільними лініями.
4. Деякі приклади застосування ППП
5. Загальне формулювання і приклади задач лінійного програмування
6. Загальні вимоги до оформлення геологічних карт. Умовні позначення на геологічній графіці.
7. Класифікація і позначення світлофорів
8. Класифікація, умовні позначення та маркування
9. Конст-правовий звичай як джерело конст права в ЗК,поняття та ознаки,приклади.
10. Маркування базового позначення
11. Мови як знакові системи. Природні та формальні мови. Алгоритмічні мови та мови програмування як приклади формальних мов.
12. НА ПОЗНАЧЕННЯ ІСТОТ / НЕІСТОТ

Переглядів: 1840