
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Поперечного перерізу
Напруження і деформації в стержнях некруглого
Розрахунки на міцність і жорсткість
Епюри крутних моментів
Для розрахунку бруса на кручення (формули 7.7-7.12) необхідно знати величину крутного моменту Мх в будь-якому поперечному перерізі бруса. Закон зміни крутних моментів по довжині бруса Мх(х) називають епюрою крутних моментів. Епюра дає наочне зображення розподілу крутних моментів вздовж осі бруса. Величину Мх знаходять із умови рівноваги будь-якої частини бруса, розміщеної з одного боку від перерізу. Із рівняння рівноваги (1.7) випливає, що крутний момент у будь-якому поперечному перерізі чисельно дорівнює алгебраїчній сумі зовнішніх моментів, прикладених до бруса справа або зліва від перерізу.
Епюри крутних моментів дають змогу визначити небезпечні перерізи, зокрема, якщо брус має сталий поперечний переріз, то небезпечними будуть перерізи на ділянці, де виникає найбільший крутний момент.
Крутний момент вважають додатним, якщо результувальний момент зовнішніх пар, прикладених до розглядуваної частини бруса буде
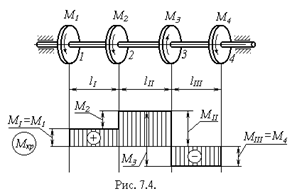
| напрямлений за стрілкою годинника, коли дивитися в торець перерізу, і навпаки. Користуючись принципом пом’якшених граничних умов, вважатимемо, що у поперечному перерізі, де прикладений скручувальний момент, значення крутного моменту змінюється стрибкоподібно. При побудові епюри крутних моментів їх величини відкладають |
перпендикулярно прямій, паралельній осі бруса (базі епюри). На рисунку 7.4 приведений приклад побудови епюри крутних моментів.
Для нормальної роботи стержнів на кручення необхідно задовольнити:
умову міцності
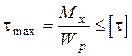 (7.13)
(7.13)
умову жорсткості
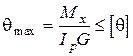 (7.14)
(7.14)
де [t] - допустиме напруження кручення, яке вибирають залежно від допустимого напруження на розтяг, умов роботи конструкції та інше. Наприклад:
для сталей
[t]=(0,55...0,60)[s]р,
для чавунів
[t]=(1,0...1,2)[s]р.
В формулі (7.14) [q] - допустимий кут закручування, нормований технічними умовами.
Для вала суцільного поперечного перерізу
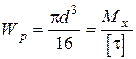 , звідки
, звідки
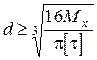 .
.
Для трубчастого вала
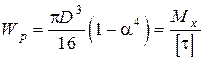 , звідки
, звідки
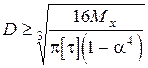
де a=d/D.
При розрахунках на жорсткість, враховуючи (7.14) і значення Ip для суцільного вала 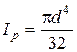 ,
,
для трубчастого вала 
знаходимо:
для суцільного вала
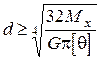
для трубчастого вала

Таким чином діаметр вала визначають з умови міцності (7.13) та умови жорсткості (7.14). За кінцевий розмір беруть більший діаметр.
Часто скручувальні моменти визначають за потужністю N, що передається на вал або знімається з нього і за його кутовою швидкістю w. У такому випадку скручувальний момент визначають за формулою
 . (7.15)
. (7.15)
Якщо N взяти в ватах, а w - у радіанах за секунду, то Мк буде в Нм.
В теорії кручення брусів некруглого поперечного перерізу гіпотеза плоских перерізів не виконується, оскільки в процесі деформації
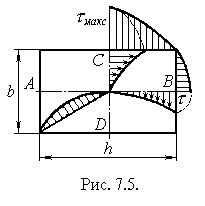
| поперечні перерізи таких брусів не залишаються плоскими і викривляються, приймаючи форму криволінійної поверхні. В зв’язку з цим задача з визначення напружень і деформацій не може бути розв’язана методами опору матеріалів. На рисунку 7.5 показана епюра розподілу напружень по прямокутному перерізі, при крученні, отримана методами теорії пружності. Як видно із рисунку 7.5 найбільші напруження |
будуть в точках А, А1, розміщених по середині довгих сторін. Їх можна визначити за формулою
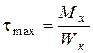 , (7.16)
, (7.16)
де
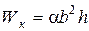 . (7.17)
. (7.17)
В точках В і В1 напруження
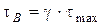 . (7.18)
. (7.18)
Кут закручування стержня
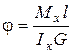 , (7.19)
, (7.19)
де 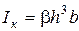 . (7.20)
. (7.20)
Коефіцієнти a, b, g залежать від відношення h/b і приводяться в таблиці
| h/b | 1.0 | 1.5 | 1.75 | 2.0 | 2.5 | |||||
| a | 0.208 | 0.231 | 0.239 | 0.246 | 0.258 | 0.267 | 0.282 | 0.299 | 0.307 | 0.313 |
| b | 0.141 | 0.196 | 0.214 | 0.229 | 0.249 | 0.263 | 0.281 | 0.299 | 0.307 | 0.313 |
| g | 0.859 | 0.820 | 0.795 | 0.766 | 0.753 | 0.745 | 0.743 | 0.742 | 0.742 |
Iк ,Wк - називають моментом інерції і моментом опору при крученні.
Запишемо умови міцності та жорсткості для прямокутного перерізу:
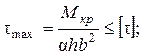
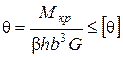
Якщо має місце кручення стержня складного перерізу, який можна розбити на частини із прямокутних елементів, то для нього
 ,
,
де і = 1, 2, 3, …, n - номери елементарних частин, на які розбитий переріз.
Оскільки кут закручування для всього перерізу і всіх його частин однаковий, то крутний момент розподіляється між окремими частинами перерізу пропорційно їх жорсткостям. Найбільшого значення напруження t досягає для того елемента, в якого  буде максимальне
буде максимальне
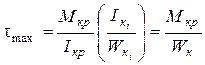 ,
,
де 
Читайте також:
- Вибір перерізу провідників у мережах напругою до 1000 В з урахуванням плавких запобіжників
- Вибір перерізу провідників у мережах напругою до 1000В з урахуванням автоматичних вимикачів і теплових реле
- Визначення потрібної площі перерізу стояка.
- Геометричні характеристики поперечного перерізу
- Головні осі інерції та головні моменти інерції перерізу
- Головні осі інерції та головні моменти інерції перерізу
- Елементи поперечного профілю та їхнє призначення
- Заклепка – стержень круглого поперечного перерізу з голівкою на кінці.
- Круглого поперечного перерізу
- Круглого поперечного перерізу
- Моменти інерції перерізу
- Основні параметри поперечного профілю доріг
| <== попередня сторінка | | | наступна сторінка ==> |
| Круглого поперечного перерізу | | | Основні поняття |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |