• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Приклади

14. У люстрі три лампи. Ймовірність виходу з ладу про­тягом року для кожної лампи дорівнює 0,2. Яка ймовір­ність того, що протягом року доведеться замінити не мен­ше двох ламп?

Скористаємось формулою (17). Ймовірність того, що про­тягом року вийде з ладу три лампи, дорівнює 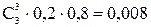дві лампи — .За теоремою додавання для несумісних подій шукана ймовір­ність дорівнює Р₃ (2) + P₃ (3)= 0,096 + 0,008 = 0,104.

15. Знайти ймовірність того, що з 500 висіяних насінин не зійде 130, якщо схожість насіння оцінюється ймовірніс­тю 0,75.

Маємо р = 0,25, q = 0,75, n = 500, k = 130. Зручно скористатися формулою Лапласа. Отже, , .

За таблицею значень функції j(x) знаходимо j(0,52) = 0,3485. Тоді за формулою (19) дістаємо P₅₀₀ (130)»0,036.

16. При виготовленні деякої масової продукції ймовір­ність появи одного нестандартного виробу дорівнює 0,01. Яка ймовірність того, що в партії із 100 виробів 4 будуть нестандартними?

У даному випадку ймовірність р = 0,01 мала, а число n = 100 велике, причому λ= nр= =100 × 0,01 = 1. Ко­ристуючись формулою Пуассона (21), дістаємо

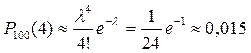
Читайте також:

1. В чому полягає явище тунелювання через потенціальний бар’єр, наведіть приклади.
2. Визначення і приклади
3. Деякі приклади застосування ППП
4. Загальне формулювання і приклади задач лінійного програмування
5. Конст-правовий звичай як джерело конст права в ЗК,поняття та ознаки,приклади.
6. Мови як знакові системи. Природні та формальні мови. Алгоритмічні мови та мови програмування як приклади формальних мов.
7. Наведіть приклади переслідування української мови царизмом у ХІХ ст.
8. Наведіть приклади різних класифікацій жанрів. Яке місце в них відведено сатиричним жанрам?
9. Наведіть приклади різних класифікацій жанрів. Яке місце в них відведено сатиричним жанрам?
10. Наведіть приклади українського національного відродження в першій половині ХІХ ст.
11. Нижче наведені приклади програмних завдань для трьох рівнів результатів.
12. ОСНОВНІ РІЗНОВИДИ АПАРАТІВ КЕРУВАННЯ І ПРИКЛАДИ ЇХНЬОГО ЗАСТОСУВАННЯ

Переглядів: 1047