Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

І. Модель Леонтьєва багатогалузевої економіки

Лінійні економічні моделі

Граничні норми підіймання та переміщення важких предметів неповнолітніми

Забороняється також залучати неповнолітніх до підіймання і переміщення речей, маса яких перевищує встановлені для них граничні норми.

Вік неповнолітніх,

у роках Граничні норми ваги вантажу, кг

Короткочасова робота Тривала робота

Юнаки Дівчата Юнаки Дівчата

14 5 2,5 — —

15 12 6 8,4 4,2

16 14 7 11,2 5,6

17 16 8 12,6 6,3

Усі особи, молодші вісімнадцяти років, приймаються на роботу лише після попереднього медичного огляду й у подальшому, до досягнення 21 року, щороку підлягають обов’язковому медичному огляду.

За згодою батьків або опікунів можуть, як виняток, прийматись на роботу особи, які досягли п’ятнадцяти років.

Забороняється залучати неповнолітніх до нічних, надурочних робіт та робіт у вихідні дні (ст. 192 КЗпП).

Тривалість робочого часу для неповнолітніх працівників:

- віком від 16 до 18 років - 36 годин на тиждень;

- віком від 15 до 16 років – 24 години на тиждень.

Щорічна відпустка неповнолітнім надається в літній час або, за їх бажанням, у будь-яку пору року.

Звільнення неповнолітніх з ініціативи власника або уповноваженого ним органу, крім дотримання загального порядку звільнення, здійснюється тільки за згодою районної (міської) комісії у справах неповнолітніх (ст. 198 КЗпП).

( балансовий аналіз )

Розглянемо спрощену економіко-математичну модель міжгалузевого балансу. Зв’язок між галузями зазвичай відображають у таблицях міжгалузевого балансу, а математичну модель, яка дає змогу аналізувати їх, розроблено в 1936 р. Американським економістом В.Леонтьєвим.

Припустимо, що весь виробничий комплекс поділено на n „чистих” галузей. Чисті галузі є економічною абстракцією, тобто це умовні галузі, кожна з яких об’єднує все виробництво даного виду продукції. Вважатимемо, що кожна з галузей випускає лише один певний вид продукції (тобто різні галузі випускають різну продукцію). В процесі виробництва кожна з галузей потребує продукції, виробленої в інших галузях.

Мета балансового аналізу – відповісти на запитання, яке постає в макроекономіці й пов’язане з ефективністю ведення багатогалузевого господарства: яким має бути обсяг виробництва кожної з галузей, щоб задовольнити всі потреби в продукції цієї галузі? При цьому кожна галузь виступає, з одного боку, як виробник даної продукції, а з іншого – як споживач і своєї, і виробленої іншими галузями продукції.

Основні припущення моделі, яку надалі називатимемо моделлю Леонтьєва, такі:

1) в економічній системі виробляються, купуються, споживаються і інвестуються n видів продукції, які позначимо індексами

2) кожна галузь виробляє лише один вид продукції, отже, спільне виробництво різних товарів виключається. Різні галузі виробляють різні товари, й тому галузь, що виробляє продукцію виду i, позначатимемо тим самим індексом;

3) під виробничим процесом у кожній галузі розумітимемо перетворення деяких (можливо всіх) видів продукції, взятих у певних обсягах, на деякий обсяг продукції того чи іншого виду. При цьому припускається, що співвідношення витраченої й випущеної продукції є сталим.

Нехай економіко-виробнича система складається з n галузей, тобто виробляє n видів продукції. Схему міжгалузевого балансу виробництва й розподілу продукції подано в табл. 1, де зазначено основні показники та зв’язки виробництва за певний період часу ( зазвичай за рік ).

Введемо позначення: X_i – обсяг валової продукції і-ої галузі (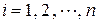) за одиницю часу, наприклад за рік; x_i _j – обсяг продукції і-ої галузі, що потребує j-та галузь у процесі виробництва (); Y_i – обсяг кінцевої продукції і-ої галузі, призначеної для невиробничого споживання.

Таблиця 1.

Галузь вироб- ництва	Розподіл випуску продукції в галузях виробництва	Обсяг кінце- вої про- дукції	Обсяг вало- вої про- дукції
		...	j	…	n	Всього
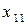
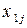
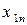
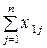
			…		…			Y₁	X₁
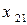
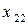
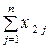
			…		…			Y₂	X₂
…	…	…	…	…	…	…	…	…	…
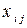
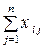
i			…		…			Y_i	X_i
…	…	…	…	…	…	…	…	…	…
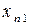
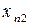
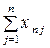
n			…		…			Y_n	X_n
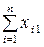
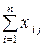
Всього			…		…			Y	X

Використовуючи дані табл. 1, запишемо квадратну матрицю п-ого порядку ( за умови рівності поданих у балансі галузей виробництва та споживачів продукції). Кожен елемент матриці x_i _j, i=1, 2,…,n; j=1, 2,…,n характеризує обсяг поставки продукції з і-ої галузі, що йде на виробниче споживання в j-ій галузі. Взявши суму міжгалузевих поставок продукції і-ої галузі в усіх галузях-споживачах, дістанемо загальний обсяг проміжної продукції і-ої галузі: i=1, 2,…,n.

Сума обсягів проміжної продукції всіх галузей виробництва становить загальний обсяг проміжної продукції .

За економічним змістом обсяг проміжної продукції – частина обсягу валової продукції, яка залишається після вилучення кінцевого продукту й спрямовується для відшкодування поточних матеріальних витрат у межах розглядуваного періоду часу. Оскільки обсяг валової продукції будь-якої і-ої галузі дорівнює сукупному обсягові продукції, що споживається п галузями, та кінцевої продукції, то запишемо систему

(1)

або а скороченій формі:

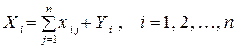. (2)

Рівняння (1) наз. співвідношеннями балансу.

Розглянемо міжгалузевий баланс у вартісній формі, тобто коли всі величини, що входять у систему (1), виражають вартість.

Особливість системи (1) полягає в тому, що змінні в ній містяться в першому степені, тому залежність між обсягом валової продукції та розподілом продукції кожної галузі лінійна.

Зауважимо, що величини можуть виражатись в натуральних одиницях (штуках, тоннах, літрах тощо). Тоді йдеться про міжгалузевий баланс у натуральній формі.

Під час побудови й практичних застосувань економіко-математичної моделі міжгалузевого балансу використовують коефіцієнти прямих матеріальних витрат. Якщо обсяг міжгалузевих поставок і-ої галузі в j-ту поділити на обсяг валової продукції j-ої галузі, дістанемо шуканий норматив:

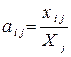, , (3)

де 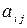- коефіцієнт прямих витрат продукції і-ої галузі на одиницю обсягу валової продукції j-ої галузі.

Ці коефіцієнти утворюють квадратну матрицю коефіцієнтів прямих витрат

,

яку іноді називають матрицею технологічних коефіцієнтів (технологічною матрицею).

Матриця А містить інформацію про структуру міжгалузевих зв’язків, про технологію виробництва даної економіко-виробничої системи. З рівності (3) випливає, що

. (4)

Підставивши (4) в ( 3), дістанемо систему

, . (5)

Запишемо її в матричній формі

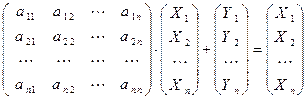, або

X=AX+Y (6)

Співвідношення (6) називаються рівнянням лінійного міжгалузевого балансу, або моделлю Леонтьєва.

Основна задача міжгалузевого балансу полягає у відшуканні такої матриці обсягів валової продукції Х, яка за відомої матриці прямих витрат А забезпечує задану матрицю обсягів кінцевої продукції Y.

Перепишемо рівняння (6) так:

(E-A)X=Y. (7)

Якщо матриця (Е-А) невироджена, то його можна подати у вигляді

X=(E-A)^-1Y. (8)

Матрицю В=(Е – А ) ^{- 1} називають матрицею повних витрат.

Економічний зміст елементів матриці В такий: кожен елемент b_i _j матриці Вє обсягом валової продукції і-ої галузі необхідної для забезпечення випуску одиниці кінцевої продукції j-ої галузі( i, j=1,2,…,n).

За економічним змістом задачі величини X_i мають бути невід’ємними, оскільки Y_i ≥ 0 i a_i _j ≥ 0, де i, j=1,2,…,n.

З математичного погляду питання про сумісність системи (6) зводиться до питання про існування оберненої матриці (Е – А ) ^{– 1}, складеної з невід’ємних елементів.

Рівняння міжгалузевого балансу можна використовувати у двох випадках. У першому (простішому) випадку, коли відома матриця обсягів валової продукції X, потрібно обчислити матрицю обсягів кінцевої продукції Y.

Приклад. Нехай матриця обсягів валової продукції галузі й матриця коефіцієнтів прямих витрат мають вигляд:

, .

Використовуючи формулу (7) і правило множення матриць, дістанемо матрицю обсягів кінцевої продукції, що призначена до реалізації:

.

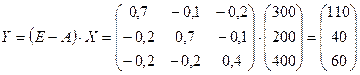У другому випадку рівняння міжгалузевого балансу використовується для планування.

Матрицю А, всі елементи якої невід’ємні, називають продуктивною, якщо для довільної матриці Y із невід’ємними елементами існує розв’язок рівняння (6) – матриця X, усі елементи якої невід’ємні. В цьому разі модель Леонтьєва називається продуктивною.

Є кілька критеріїв продуктивності матриці А. ми будемо користуватися таким: матриця А з невід’ємними елементами продуктивна, якщо максимум сум елементів її стовпців не перевищує одиниці, причому хоча б для одного із стовпців сума елементів строго менша за одиницю. Тобто матриця Апродуктивна, якщо

1. a_i _j ≥ 0, для довільних i, j=1,2,…,n;

2. , i, j=1,2,…,n;

3. існує номер j такий, що , j=1,2,…,n.

Приклад. Розглянемо умовну виробничу систему, яка складається з трьох галузей. Коефіцієнти прямих витрат одиниць продукції і-ої галузі, що використовуються для випуску одиниць продукції j-ої галузі, та обсяги кінцевої продукції (у вартісній формі) наведено в таблиці.

Галузь виробництва Прямі витрати галузей Обсяг кінцевої продукції

0,2

0,2 0,1

0,1 0,2

Визначити: коефіцієнти повних витрат; матрицю обсягів валової продукції X та план кожної галузі; коефіцієнт непрямих (посередницьких) витрат.

Позначимо матрицю обсягів валової продукції, яка визначає виробничу програму галузей, так

,

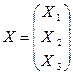де Х₁, Х₂, Х₃, - планові обсяги валової продукції галузей. У розглядуваному прикладі матрицями технологічних коефіцієнтів та обсягів кінцевої продукції є відповідно

, .

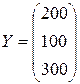Виробничі зв’язки галузей задовольняють умови

; .

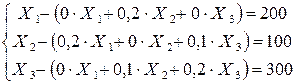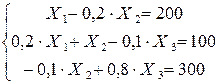Запишемо систему в матричному вигляді:

( E – A )X = Y.

Тоді

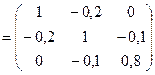
знайдемо обернену матрицю B = ( E – A ) ^-1.

Визначник матриці ( Е – А ):

.

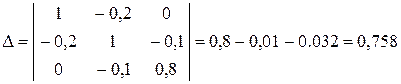Знайдемо алгебраїчні доповнення елементів матриці ( Е – А ):

B_{1 1}= 0,79; B_{2 1} = 0,16; B_{3 1} = 0,02;

B_{1 2}= 0,16; B_{2 2} = 0,8; B_{3 2} = 0,1;

B_{1 3}= 0,02; B_{2 3} = 0,1; B_{3 3} = 0,96.

Обернена матриця має вигляд:

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Конституція України (ст. 24) на вищому законодавчому рівні закріпила рівність прав жінок і чоловіків.	\|	Порядок розслідування нещасних випадків.

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.009 сек.