• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Приклади розв’язання типових задач.

План

Визначений інтеграл.

1.Визначений інтеграл.

2.Формула Ньютона-Лейбніца.

3. Основні методи обчислення визначеного інтеграла.

4. Геометричне застосування визначеного інтеграла.

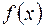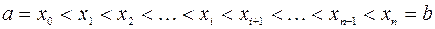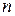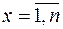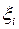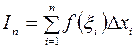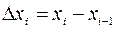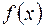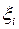1. Нехай функція визначена на відрізку і - довільне розбиття цього відрізка на частинних відрізків , . На кожному з них виберемо довільну точку і складемо суму , . Число називається інтегральною сумою функції , що відповідає даному розбиттю відрізка і вибору точок . Позначимо , .

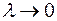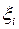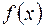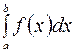Означення. Якщо існує границя інтегральної суми при , що не залежить ні від способу розбиття відрізка , ні від вибору точок , то ця границя називається визначеним інтегралом від функції на відрізку і позначається , тобто

.

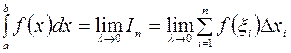Число 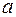називають нижньою, число - верхньою межею визначеного інтеграла.

2. Якщо 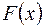- первісна для 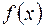, тобто 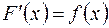на , то (формула Ньютона-Лейбніца). Різницю записують також у вигляді .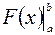

3Інтегрування частинами.Якщо 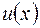і 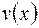- неперервно диференційовні функції на , то справедлива формула інтегрування частинами

.

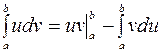Заміна змінної у визначеному інтегралі:

, де 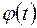- функція, неперервна разом зі своєю похідною 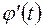на відрізку 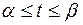; , , - функція неперервна на .

Важливо те, що заміняючи змінну у визначеному інтегралі, знаходять також нові межі інтегрування, і надалі вже не повертаються до початкової змінної.

4. Площа фігури, обмеженої кривими 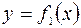і 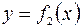та прямими 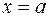і знаходиться за формулою .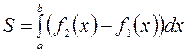

Довжина дуги кривої , 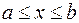знаходиться за формулою .

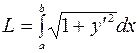Об’єм тіла, утвореного обертанням криволінійної трапеції, обмеженої лініями , , 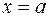, , 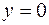навколо осі .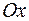

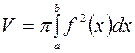За допомогою визначеного інтеграла обчислюють також статичні моменти і моменти інерції плоских фігур, знаходять координати центра мас плоскої фігури, роботу, тиск та інші величини.

Приклад 1. Обчислити .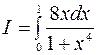

.

Приклад 2. Обчислити інтеграл .

.

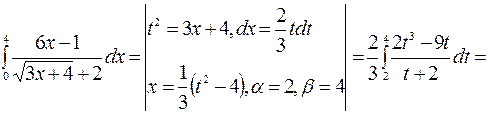
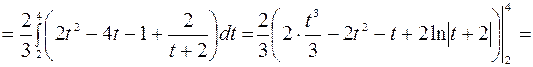
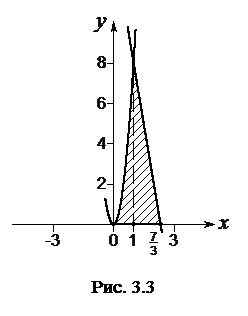
Приклад 3. Обчислити площу фігури, обмеженої заданими параболами

Знайдемо абсциси точок перетину заданих парабол. Для цього прирівняємо праві частини цих рівнянь:

Звідси

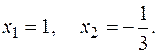
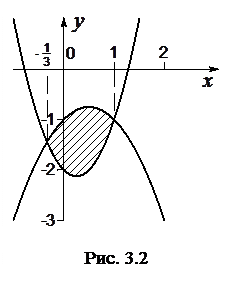Площу фігури обчислюємо за формулою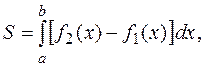

де – криві, які обмежують фігуру .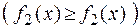

В нашому випадку маємо

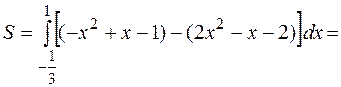
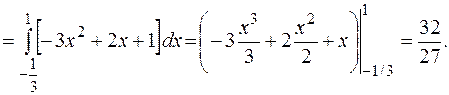
Приклад 4. Знайти об’єм тіла, утвореного обертанням навколо осі Ох фігури, розташованої в першій координатній чверті і обмеженої параболою 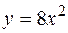, прямою і віссю Ох.

Знайдемо абсцису точки перетину параболи і прямої в першій координатній чверті. Для цього розв’яжемо рівняння

або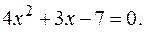

Знаходимо, що Першій координатній чверті відповідає корінь

Абсцису точки перетину прямої з віссю Ох знайдемо, розв’язавши рівняння 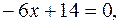звідки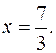

Таким чином, можемо вважати, що тіло обертання обмежене при 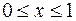поверхнею, яка утворена обертанням параболи 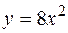навколо вісі Ох, а при – обертанням прямої .

Читайте також:

1. IV. Перевірка розв’язання і відповідь
2. Алгоритм розв’язання задачі
3. Алгоритм розв’язання розподільної задачі
4. Аналітичний розрахунок сумарного завантаження типових перетинань
5. Б. Англо-український глосарій типових конструкцій з військового перекладу 1 страница
6. Б. Англо-український глосарій типових конструкцій з військового перекладу 2 страница
7. Б. Англо-український глосарій типових конструкцій з військового перекладу 3 страница
8. Будова типових кондуктометричних чарунок
9. В чому полягає явище тунелювання через потенціальний бар’єр, наведіть приклади.
10. Визначення і приклади
11. Визначення оптимального варіанта розв’язання проблеми на основі порівняльного аналізу можливих варіантів
12. Визначення проблеми, на розв’язання якої спрямована Програма

Переглядів: 1826