
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Теорема множення ймовірностей для залежних подій
Подія В називається залежною від події А, якщо ймовірність події В залежить від того, відбулась чи ні подія А. Умовна ймовірність події В при умові, що подія А відбулась, позначається Р(В/А).
Ймовірність спільної появи (добутку) двох залежних подій А і В дорівнює добутку ймовірності однієї із них на умовну ймовірність іншої при умові, що перша подія відбулась, тобто
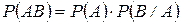 .
.
З іншої сторони

Так як

то

Повторні незалежні випробування.
При повторних незалежних випробуваннях, в яких ймовірність появи події А залишається сталою, користуються формулою Бернуллі.
Ймовірність того, що в n незалежних повторних випробуванях подія А буде мати місце m разів (m £ n), визначається формулою Бернуллі:
 ( закон Бернуллі),
( закон Бернуллі),
де 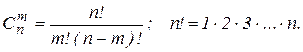
p – ймовірність появи події А в одному випробуванні;
q = 1 – р.
При великій кількості повторних випробувань користуватись формулою Бернуллі не зручно, так як розрахунки стають громіздкими. В таких випадках користуються асимптотичними формулами, які дають достатньо точні результати.
За теоремою Муавра-Лапласа для великої кількості незалежних повторних випробувань:

де

Функцїя φ (х) парна, тобто φ (-х) = φ(х) .
Значення функції φ(х) для додатніх значень аргумента х приведені в таблиці (Лобоцька , додаток 1).
При великих n (n~102–103) і малих p (р<<1) користуються асимптотичною формулою Пуасcона:
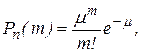
де µ = np і повинно бути меншим або рівним 10.
Дане співвідношення в літературі часто називають законом Пуасcона або законом рідкісних подій.
Для великих значень µ рекомендується користуватись теоремою Муавра-Лапласа.
Випадковою величиною називають змінну величину, яка може приймати, в залежності від випадкового збігу обставин, ті чи інші числові значення з певними ймовірностями.
Випадкова величина в результаті одного випробування (спостереження, вимірювання) прийме одне із можливих значень.
Приклади випадкових величин є: тривалість життя людини, кількість хворих на диспансерному обліку, вміст гемоглобіну в крові хворого та багато інших показників.
Випадкові величини позначають великими буквами латинського алфавіту X , Y , Z , … , а їх можливі значення x, y, z, … або х1 , х2 , … .
Ймовірність значень випадкової величини позначають:
Р (Х = х1) = Р (х1) = p1 і т.д.
Всі випадкові велчини поділяють на дискретні і неперервні.
Дискретною називають випадкову величину, яка приймає окремі можливі значення (значення, які можна пронумерувати) з певними ймовірностями.
Число можливих значень випадкової дискретної величини може бути скінченим або нескінченим.
Дискретні випадкові величини можуть мати чисельні значення, як цілі так і дробові, як додатні так і від’ємні. На практиці часто приходиться мати справу з дискретними випадковими величинами, які приймають лише цілі додатні значення. Наприклад, кількість хворих в районній лікарні з тим або іншим захворюванням, кількість викликів швидкої допомоги за добу і т.п.
Неперервною називають випадкову величину, яка може приймати довільні значення із деякого скінченого або нескінченого інтервалу.
Число можливих значень неперервної випадкової величини завжди нескінчене, її значення неможливо пронумерувати.
Наприклад, температура тіла людини під час інфекційного захворювання, маса людини в тому чи іншому віці і т.т.
Характеристики дискретної випадкової величини
Дискретна випадкова величина Х вважається заданою, якщо вказані всі її можливі значення і ймовірності, з якими вона може приймати дані значення.
Законом розподілу дискретної величини називають відповідність між її можливими значеннями і їх ймовірностями.
Таку відповідність задають у вигляді таблиці.
| Х | х1 | х2 | … | хі | … | хn |
| p | p1 | p2 | … | pі | … | pn |
Так як в результаті одного випробування випадкова величина Х завжди приймає одне із всіх можливих значень х1 , х2 , … , хn , то випадкові події Х = х1 , Х = х2 , … , Х = хn утворюють повну групу подій і :
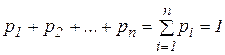 (умова нормування закону розподілу)
(умова нормування закону розподілу)
Поряд із законом розподілу випадкову величину описують числовими характеристиками: 1) математичним сподіванням; 2) модою; 3) дисперсією;
4) середнім квадратичним відхиленням.
Математичним сподіванням дискретної випадкової величини Х називають суму добутків всіх можливих значень величини Х на їх ймовірності.
Математичне сподівання позначають М (Х) або µ :

Математичне сподівання наближено рівне середньому арифметичному значенню випадкової величини визначається за результатами серії випробувань:
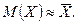
Причому, така рівність тим точніша, чим більше число n проведених випробувань, спостережень або вимірювань.
В граничному випадку виконується рівність:

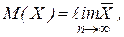 де n кількість випробувань.
де n кількість випробувань.
Математичне сподівання випадкової величини Х називають центром розподілу.
Близькою до математичного сподівання є мода як числова характеристика випадкової величини.
Модою Мо дискретної випадкової величини називають таке значення xm випадкової величини, що попереднє і наступне за ним значення мають ймовірності, менші від Р(xm).
Розподіли випадкових величин можуть мати одну, дві або більше мод.
В медико-біологічних дослідженнях часто знаходять не математичне сподівання, а моду. В медицині, наприклад, знання середнього віку дітей, що хворіють ангіною, менше цікаве, ніж знання віку, в якому частіше всього спостерігається захворювання.
Розсіювання відхилень значень випадкової величини відносно математичного сподівання характеризують дисперсія і середнє квадратичне відхилення.
Дисперсією дискретної випадкової величини називають математичне сподівання квадрату різниці значення випадкової величини Х і її математичного сподівання μ.
Дисперсію позначають D(X):
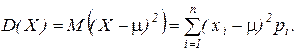
Використовуючи властивості математичного сподівання можна показати, що:

Дисперсія має розмірність квадрату випадкової величини.
Середнім квадратичним відхиленням випадкової величини називають корень квадратний із її дисперсії:

Приклад розрахунку числових характеристик дискретної випадкової величини, заданої законом розподілу:
| Х | 1 | 2 | 3 | 4 | 5 |
| р | 0,15 | 0,3 | 0,4 | 0,1 | 0,05 |
Умова нормування: 


1. Математичне сподівання:
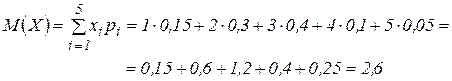
2. Мода: М0(Х) = 3.
3. Дисперсія:

4. Середнє квадратичне відхилення:

Якщо дискретна випадкова величина Х – число появи події А в n незалежних повторних випробуваннях. Причому в кожному випробуванні 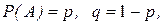 то величина Х підлягає розподілу Бернуллі
то величина Х підлягає розподілу Бернуллі

Числові характеристики величини Х: 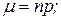
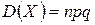
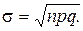
Якщо число незалежних повторних випробувань n велике, а p<<1, q =
=1 - p ≈ 1, то користуються розподілом Пуассона
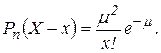
При цьому числові характеристики величини Х визначаються за формулами:
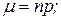


Характеристики неперервної випадкової величини.
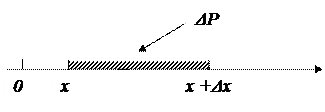
Ймовірність ΔР того, що неперервна випадкова величина Х приймає значення в інтервалі (х, х +Δх) прямо пропорційна ширині інтервалу Δх:
ΔP = ƒ(x)Δx,
 |
|
де f(x) – коефіцієнт пропорційності, який називають функцією щільності густини розподілу ймовірності або щільністю густиною ймовірності:
 .
.
Для безмежно малого інтервалу: 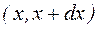
dP= ƒ (x)dx; 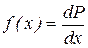 .
.
Функція щільності густини ймовірності значень неперервної випадкової величини є аналогом закону розподілу для дискретної випадкової величини.
Функція щільності густини ймовірності має властивості:
1. ƒ(x) ≥ 0 при - ∞ < x < +∞, ƒ (- ∞) = 0, ƒ (+ ∞) = 0.
2.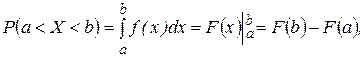
де 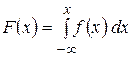 - функція розподілу випадкової величини Х.
- функція розподілу випадкової величини Х.
F(x) = P(X<x). Так як 0 ≤ Р ≤ 1, то 0 ≤ F(х) ≤1.
 |
 |
3. Умова нормування для щільності густини ймовірності як наслідок властивості №2.
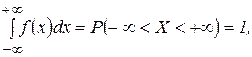

Площа під графіком функції f(x) повинна дорівнювати одиниці.
Числові характеристики неперервної випадкової величини Х
Математичне сподівання неперервної випадкової величини Х:
 де f(x) – густина ймовірності.
де f(x) – густина ймовірності.
Дисперсія неперервної випадкової величини Х:

Середнє квадратичне відхилення:

Більшість неперервних випадкових величин в природі розподілені за так званим нормальним законом розподілу (законом Гауса).
Закон розподілу неперервної випадкової величини Х вважається нормальним, якщо густина ймовірності її значень має вигляд:

де х – значення випадкової величини;
σ - середнє квадратичне відхилення;
μ - математичне сподівання або центр розподілу. 
Графік функції f(x) називають нормальною кривою розподілу або кривою Гауса.
В точці А, в якій х = μ, функція має максимум:

Точки В і С, для яких х = μ –σ і х = μ +σ відповідно , є точками перегину.



Нормальний розподіл залежить від параметрів μ і σ .
Нормальний розподіл з параметрами: μ=0 і σ=1, називають нормованими або стандартними.
При цьому:


Функція розподілу для нормально розподіленої випадкової величини Х:
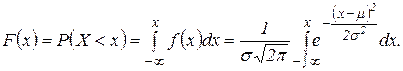
Функція розподілу для нормованої випадкової величини: 
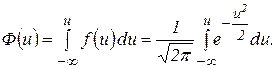
Функції F(x) і Ф(u) є тотожніми, тобто
F(x) = Ф(u).
Функція Ф(u) має таку властивість:
Ф(u)+Ф(-u) = 1,
звідки 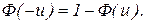
Для додатніх значень u складена таблиця значень функції розподілу Ф(u).
Ймовірність попадання нормально розподіленої випадкової вклични Х в заданий інтервал (х1 , х2) визначаеться співвідношенням :
P(x1<X<x2) = Ф(u2)-Ф(u1),
де 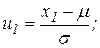
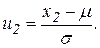
Підрахуємо ймовірність попадання нормально розподіленої випадкової величини Х в інтервали:
1) (μ – σ , μ +σ) ;
2) (μ - 2σ , μ + 2σ) ;
3) (μ - 3σ , μ + 3σ) .
Користуючись попередніми співвідношеннями і таблицею значень функції
Ф(u), отримаємо:
1) 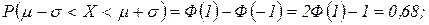
2) 
3)
Тобто, ймовірність попадання нормально розподіленої неперервної випадкової величини в інтервалі відповідно дорівнюють:
1) μ 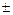 σ, Р1 = 0,68;
σ, Р1 = 0,68;
2) μ 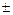 2σ, Р2 = 0,95;
2σ, Р2 = 0,95;
3) μ 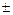 3σ, Р3 = 0,997;
3σ, Р3 = 0,997;
З останнього випливає, що неперервна випадкова величина Х, яка розподілена за нормальним законом, з ймовірністю Р = 0,997 приймає значення в інтервалі μ±3σ, тобто значення випадкової величини практично не виходять за інтервал μ±3σ. (Правило “3σ”) . Графічно це означає:
 |
Інші закони розподілу неперервних величин
Розподіл Максвелла визначає густину ймовірності для модуля швидкості v молекул газу.

де m0 – маса молекули; k– стала Больцмана; Т – абсолютна температура газу.
Розподіл Больцмана визначає густину ймовірності знаходження молекули газу в однорідному гравітаційному полі.

Іноді розподілом Больцмана називають залежність концентрації молекул газу (повітря) від висоти h.
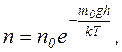
де n0 – концентрація молекул газу на висоті h = 0.
Читайте також:
- Аксіоми додавання і множення
- Алгебра випадкових подій
- Алгебра подій
- Безвілля, його заподій і переборення.
- Безстатеве розмноження та його біологічне значення
- Безстатеве розмноження, його визначення та загальна характеристика. Спори — клітини безстатевого розмноження, способи утворення і типи спор.
- В. Друга теорема про розклад.
- Види випадкових подій
- Визначення базисних подій. Ідентифікація ризику.
- Визначення добутку на множині цілих невід’ємних чисел, його існування та єдиність. Операція множення та її основні властивості (закони).
- Виникнення Народного Руху України за перебудову. Роль цієї організації у розвиткові політичних подій в республіці протягом 1989-1991 р.
- Випадок непов’язаних(незалежних) вибірок
| <== попередня сторінка | | | наступна сторінка ==> |
| Властивості ймовірностей | | | Робота в малих групах |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |