Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Інтерполяційна формула Лагранжа.

Постановка задачі

Задача апроксимації (наближення) функції f(x) на відрізку [a, b] полягає у заміні цієї функції іншою функцією g(x), яка наближено (у певному розумінні) дорівнює f(x) на відрізку, що розглядається. У цьому випадку g(x) називається апроксимуючою функцією.

Уточнимо:

Апроксимуюча функція g(x ) може належати, наприклад,
класу алгебраїчних многочленів: ,
Класу тригонометричних поліномів:

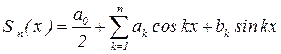
Уточнимо, що розуміється під“найкращим наближенням”, наприклад,

1)якщо g(x) співпадає з f(x) на заданій системі точок 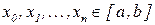, тобто
,
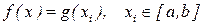то це задача інтерполювання;

2)якщо середнє квадратичне відхилення значення g(x) від значення f(x) є мінімальним
на заданій системі точок ,
або на всьому відрізку ,
- то це задача квадратичної апроксимації;

3)Якщо 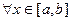функція g(x) відрізняється f(x) на величину, абсолютне значення якої не перевищує заданого числа :,
- то це задача рівномірного наближення функції.

2. Задача інтерполювання алгебраїчними многочленами.

Нехай значення 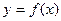задані в точках 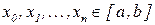і

Розглядається наступна інтерполяційна задача:

побудувати такий многочлен 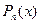(степеня не вище за n), значення якого в точках 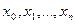, що називаються вузлами інтерполяції, співпадали би із значеннями в них функції f(x).

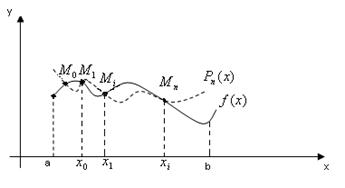
Геометричний зміст: знаходиться такий многочлен 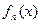, графік якого проходив би через точки , що лежать на графіку функції 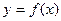, абсциси яких відповідно . Наближення функції f(x) інтерполяційним многочленом 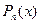на практиці застосовують не тільки тоді коли значення функції f(x) відомі лише в деяких точках, але й тоді, коли відома в кожній точці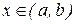, і її аналітичний вираз настільки складний, що викликає значні труднощі при розв’язуванні конкретної задачі, де приймає участь функція . В цьому випадку часто буває доцільним замінити її інтерполяційним многочленом, що співпадає з тільки на деякій системі точок, а інших точках 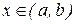лише наближено дорівнює .

Теоретичною базою можливості побудови многочлена 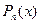при достатньо великій кількості вузлів інтерполяцій (а отже і степені многочлена) так, щоб точність наближення була як завгодно високою є

Теорема Вейєрштрассе. Якщо неперервна на відрізку [a,b], то 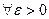знайдеться такий поліном 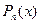достатньо великого степеня n , що

Відмітимо, що з цієї теореми відразу випливає і можливість рівномірного наближення функцій в класі алгебраїчних многочленів.

Отже маємо побудувати многочлен (1)

що задовольняє умовам

(2)

Очевидно, що невідомі коефіцієнти многочленна (1) можна знайти з системи рівнянь

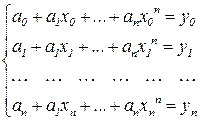
Визначником цієї системи є

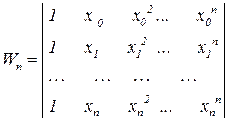визначник Вандермонда

Цей визначник, якщо тільки ніколи не дорівнює 0. Тому СЛАР має єдиний розв’язок. І знайшовши невідомі коефіцієнти , можна записати інтерполяційний поліном.

Але така побудова інтерполяційного полінома при великому числі вузлів інтерполяції викликає значні труднощі, так як потрібно розв’язувати СЛАР великого порядку.

Далі розглянемо більш прості в практичній реалізації методи побудови .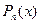

Безпосередньою перевіркою можна переконатися що многочлен

(3)

розв’язує поставлену інтерполяційну задачу, так як на даній системі точок

приймає значення відповідно . Формула (3) має назву інтерполяційної формули Лагранжа, а побудований многочлен – многочленом Лагранжа , часто він позначається . Можна показати, що є єдиним многочленом, 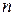-го степеня що задовольняє умові (2)

Різниця називається похибкою інтерполювання.

Доведено, що де .

Для запису інтерполяційного многочленна Лагранжа зручно користуватися таблицею

… … … … … … … … … ... ... …

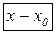
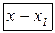
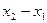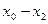
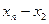
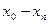
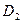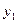
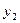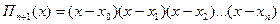
Тут - добуток елементів і - го рядка, 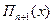- добуток елементів головної діагоналі.

Тоді многочлен Лагранжа може бути записаний так:

(4)

Приклад1. Побудувати многочлен Лагранжа 3-го степеня для функції y=f(x)

заданою таблицею. Обчислити f(2.5)

i 0 1 2 3

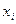
2 3 4 5

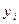
7 5 8 7

Розв’язання. Побудуємо таблицю

x-2 -1 -2 -3 -6(x-2) 7

1 x-3 -1 -2 2(x-3) 5

2 1 x-4 -1 -2(x-4) 8

3 2 1 x-5 6(x-5) 7

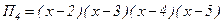
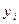
1) За формулою (4)отримаємо

2) Обчислимо значення функції

Читайте також:
Абсолютні й відносні посилання у формулах
Барометрична формула
Барометрична формула. Розподіл Больцмана частинок у зовнішньому потенціальному полі
Втрати енергії вздовж круглого трубопроводу. Формула Пуазейля і коефіцієнт Дарсі.
Загальна формула для визначення переміщень. Метод Мора
Загальна формула руху капіталу
Іякщо функція (4.24) є розв'язною відносно диференційого рівняння (4.2) при всіхзначеннях c1,…,cn, які визначяються формулами (4.26), коли т.(x,y,y`,…,y(n-1)).
Ламінарна течія рідин та газів по трубах. Формула Пуазейля
Лейкоцитарна формула у здорових людей
Лейкоцити, кількість, види.Лейкоцитарна формула
Лекція 3 Формула повної ймовірності. Формули Байєса

Переглядів: 1883

<== попередня сторінка | наступна сторінка ==>

Характеристика об’єктивної сторони адміністративного правопорушення | Інтерполяційні многочлени Ньютона.

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.007 сек.