• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Приклад 2.

Знайти мінімальне значення функції:

,

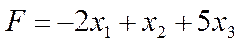за умов:

.

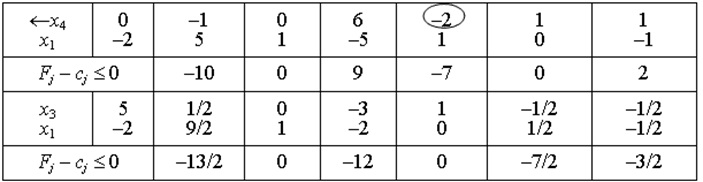
Розв’язання:

Помножимо другу нерівність на (– 1) і введемо додаткові змінні.

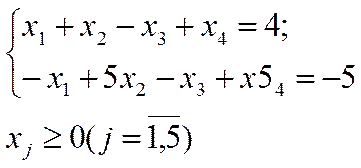
Початковий базис: вектори А₄ та А₅.

Псевдоплан: .

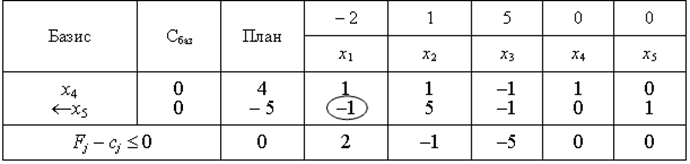
- тому виведемо вектор А₅ і змінну х₅.

Введемо – на основі розрахунку значення :

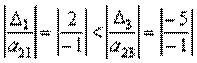, = ввести вектор А1. Розв’язувальним елементом буде а₂₁ (–1).

Оптимальний план початкової задачі:

,

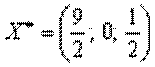та оптимальний план двоїстої задачі:

, .

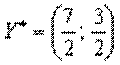3. Метод відтинаючих площин (метод Гоморі)

варіанти:

1. Перший алгоритм Гоморі для рішення повністю цілочисельних задач.

2. Другий алгоритм Гоморі для рішення частково цілочисельних задач.

Ідея розрахунків методом відтинаючих площин для розв’язання повністю цілочисельних задач (1-й метод Гоморі) полягає у такому підході:

1) лінійна задача (1)

(1)

Опорний план, який має канонічний вигляд:

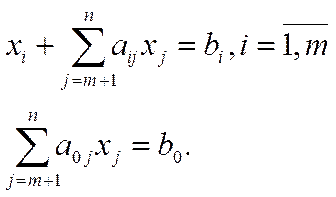(2)

2) якщо серед рівнянь-обмежень (2) є дробові значення базисних змінних x_i = b_i, то обирають серед них таке значення, яке має найбільшу дробову частину. Це рівняння

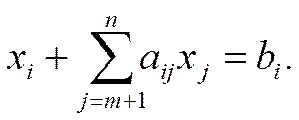
Перетворюють у додаткову нерівність:

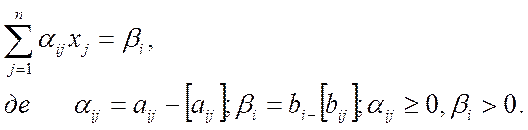(3)

Правила обрання чисел [a_ij] та [b_i]:

1. Якщо дробові числа a_ij або b_i є додатними числами, то [a_ij] та [b_i] є цілими додатними числами і дорівнюють цілій частині числа a_ij або b_i. Наприклад:

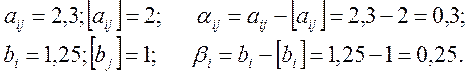
2. Якщо дрібне число a_ij або b_i є від’ємним числом, то [a_ij] та [b_i] є від’ємним цілим числом, яке за абсолютним значенням на “1” більше за абсолютне значення цілої частини числа a_ij або b_i. Наприклад:

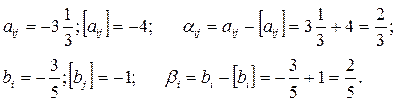
Якщо a_ij або b_i є цілими числами, то α_ij =0, β_i =0.

3. Додаткова нерівність (3) має лише додатні коефіцієнти. Вона множенням на «-1» спочатку приводиться до вигляду, який повинна мати нерівність у симплекс-методі згідно зі стандартною формою () , а потім за допомогою додаткової змінної 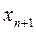перетворюється у рівняння , яке додається до оптимального опорного плану – системи (2) і разом із ним створює псевдоплан (має одне від’ємне значення ).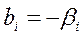

Якщо в новому оптимальному опорному плані існують базисні змінні 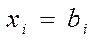, які мають дробові значення, то знов додають одне додаткове обмеження, і процес розрахунків повторюється до отримання цілочисельних значень базисних змінних.

Ознакою відсутності розв’язку задачі є наявність у таблиці хоча б одного рядка з цілими величинами a_ij та вільним дробовим членом b_i, що вказує на відсутність розв’язку в цілих числах (наприклад, ) .

Часткові цілочислові задачі (в них вимоги щодо цілочисельності ставляться лише до окремих змінних) розв’язуються так само, як попередні, за рахунок введення додаткового обмеження

,

де 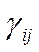- визначається з відношень:

1) для нецілочислових значень змінних :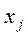

;

2) для цілочисельних значень змінних :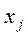

.

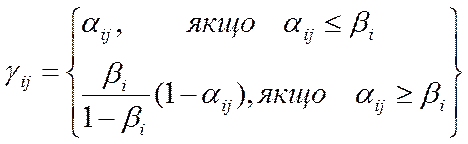Читайте також:

1. Абсолютні синоніми (наприклад, власне мовні й запозичені) в одному тексті ділового стилю вживати не рекомендується.
2. Алгоритм однофакторного дисперсійного аналізу за Фішером. Приклад
3. Базові та прикладні класифікації
4. В чому полягає явище тунелювання через потенціальний бар’єр, наведіть приклади.
5. Визначення і приклади
6. Врахування витраті втрат електроенергії. Приклад складання електробалансу.
7. Головною метою наукової діяльності в системі вищої освіти повинен стати розвиток фундаментальних та приклад­них досліджень.
8. Деякі приклади застосування ППП
9. Дієслова з префіксом дис-виражають значення ліквідації дії, названої безпрефіксним дієсловом, наприклад: гармонізувати – дисгармонізувати, асоціювати – дисасоціювати.
10. Для одиничного і дрібносерійного виробництва норма витрати визначається як укрупнена, наприклад, на 1000 станко-годин роботи даного виду роботи устаткування
11. Додаток И - Приклад виконання ремонтного креслення деталі
12. Етикет – (прикріплювати) установлений порядок поведінки в товаристві, певному оточенні, наприклад, придворний етикет, дипломатичний етикет.

Переглядів: 765