
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
У ТЕХНОЛОГІЇ БЕТОНУ
ЗАСТОСУВАННЯ МАТЕМАТИЧНИХ МЕТОДІВ
Лекція 24.
З кожним роком збільшується різноманітність бетонів, розширюються області їхнього застосування, запропоновані до бетонів вимоги, сировинна база виробництва. У технології бетону переходять до багатокомпонентних рецептур із добавками-регуляторами, використовують нові фізико-хімічні процеси, застосовують складне устаткування з елементами автоматизації. У цих умовах керування якістю й виробництвом бетону ускладнюється. Вибір оптимальних рішень потребує широкого застосування математичних методів, що дозволяють оцінювати варіанти і порівнювати їх між собою.
За допомогою математичних методів можна досліджувати й аналізувати визначені складні системи, що включають багато елементів і зв'язків, і на основі подібного аналізу відшукувати рішення, що щонайкраще задовольняють поставленим цілям. Одержання бетону з визначеним комплексом властивостей залежить від багатьох технологічних факторів, що можна розділити на п'ять основних груп. У кожну групу входить декілька технологічних факторів, число яких визначається умовами розв'язуваної задачі. Наприклад, фактори групи, що визначають режим перемішування, можуть включати в найпростішому випадку час і швидкість перемішування або враховувати енергію перемішування на одиницю маси, температуру суміші, конструктивні особливості змішувача й ін.
Загальне число технологічних факторів, що роблять вплив на властивості бетону, може бути дуже великим. У цьому випадку успішне керування технологією, що розуміє вплив найбільше істотних факторів і цілеспрямований вплив на них із метою досягнення заданих властивостей бетону або рішення інших задач, без аналізу даної системи за допомогою математичних методів практично неможливо, тим більше, що при дослідженні й аналізі системи доводиться враховувати не тільки прямий вплив технологічних факторів на властивості бетону, але й зворотний вплив проектованих властивостей на призначення того або іншого технологічного параметра, а також взаємодію факторів усередині й між окремими групами.
Для успішного застосування математичних методів і керування технологією бетону велике значення мають правильна оцінка технологічних факторів і вибір відповідних, критеріїв. У ряді випадків це потребує удосконалювання існуючих методик визначення властивостей матеріалів і параметрів технологічних процесів, розробки таких методів випробувань і вибору параметрів і характеристик матеріалів, що відповідають по точності й достовірності застосовуваним методам математичних досліджень і аналізу технологічних систем.
Системи можна розділити на два класи: детерміновані й стохастичні, хоча у практиці виробництва досліджувані системи часто не діляться настільки чітко.
До детермінованих відносять системи, у яких складові частини взаємодіють точно передбаченим чином. При дослідженні детермінованої системи не виникає ніякої непевності. Зміна одного з елементів системи на деяку величину завжди викликає зміну іншого або інших на строго визначену величину. У термінах технології бетону це відповідає висловленню: якщо величина якогось технологічного фактора Xi зміниться на ΔXi, то властивість Yi завжди зміниться на ΔYi. Окремі підсистеми технології бетону можна віднести до детермінованих, наприклад зменшення діаметра зерен (у вигляді кулі) призводить до збільшення їхньої питомої поверхні.
Для стохастичної (імовірнісної) системи не можна зробити точного детального завбачення. Таку систему можна старанно досліджувати й встановити з великим ступенем можливості, як вона буде себе поводити в будь-яких заданих умовах. Проте система все-таки залишається невизначеною, і будь-яке завбачення щодо її поводження ніколи не може вийти з логічних рамок імовірнісних категорій, за допомогою котрих її поводження описується. У стохастичних системах зміна одного з елементів не завжди викликає зміну іншого (пов'язаного з ним), а тільки в деяких випадках: якщо Хі, змінився на ΔXi, то Yi зміниться на величину ΔYi + φ, де φ - випадкова величина. Якщо під дією випадку φ=-ΔYi , то впливу Xi на Yi взагалі в даному спостереженні виявлено не буде. У технології бетону стохастичні системи мають велике поширення. Наприклад, розподіл складових і елементів структури підпорядковується ймовірносно-статистичним закономірностям, роль випадкового ефекту зростає при збільшенні обсягів (при переході від лабораторних зразків до виробів), а також при переході від одиничної до масової продукції. У технологічній системі діє велике число взаємозалежних факторів Xi. З них тільки частину можна детерміновано врахувати, а інші фактори завжди створять випадковий ефект, тому використання стохастичних систем у технології бетону дозволяє успішно вирішувати багато задач керування якістю й виробництвом.
Керування - процес цілеспрямований. Формулювання цілі вирішується в кожному окремому випадку на основі технологічних і економічних умов. Метою може бути, наприклад, досягнення бетоном оптимальної якості й підтримка її на цьому рівні з максимальною стабільністю. Засобом до досягнення мети є керування технологічними факторами Xi, що діють у технології як у складній стохастичній системі. Наприклад, із вихідного стана О необхідно прийти до мети - одержанню заданої міцності бетону R, обираючи вид основних компонентів бетону, його рецептури, тип устаткування й режими роботи. Якщо припустити, що на підставі попереднього досвіду можна відбракувати 99,99 % варіантів, то залишаються конкуруючими біля 500 рішень. Необхідно за допомогою математичних методів оцінити, яке з цих рішень найбільшою мірою відповідає поставленої мети. Ступінь досягнення мети характеризує показник, що називають критерієм ефективності або оптимальності. У якості критерію можуть бути обрані різноманітні показники: міцність або інші властивості бетону, продуктивність заводу або цеху, собівартість продукції й ін. Вибір критерію визначається призначенням аналізованої системи. Кожному варіанту рішення відповідають визначене значення обраного критерію, і задача оптимального керування складається в тому, щоб вибрати й реалізувати такий варіант, при якому критерій має екстремальне (максимальне або мінімальне) значення за даних умов виробництва. Для визначення критерію ефективності використовують функцію J=f(X1, X2,...Xn), де X - усі фактори, що істотно впливають на досліджуваний процес. Цю функцію, звичайно, називають цільовою, а в математичній теорії експерименту - функцією відгуку. Задається лише один критерій ефективності, тому що при визначеному варіанті рішення (керування) можна домогтися екстремуму лише одного критерію і неможливо, щоб два довільно заданих критеріїв досягали екстремуму одночасно, якщо немає випадкового збігу. Це положення ілюструє рис. 24.1.
У деяких випадках можуть прийматися компромісні рішення, розташовані в зоні ΔXi, коли за рахунок деякого зниження критерію J1 досягається ріст J2. Викладене пояснює, чому не вірні вимоги такого типу: «досягти максимальної міцності бетону при мінімальній витраті цементу».

Рис. 24.1. Критерії ефективності й зона оптимальних рішень
Коректною є постановка задачі у формулюванні: «досягти максимальної міцності бетону за умови, якщо витрата цементу Ц не перевищуватиме Цкр, а технологічний параметр С не вийде за межі Скр. У такому формулюванні зазначений не тільки критерій ефективності, але і границі, у яких можуть змінюватися керовані фактори, тобто дані їхні обмеження. В усіх реальних ситуаціях на технологічні фактори накладені визначені обмеження.
Наприклад, рухливість суміші повинна бути у границях, що забезпечують її щільну укладку без розшарування, температура тепло-вологісного опрацювання бетону при атмосферному тиску не повинна бути більш 100оС і т.д. Крім того, звичайно мають місце обмеження матеріальних ресурсів (кількість і якість сировини, типи устаткування, фінансові і трудові можливості і т.д.) і часу для досягнення мети.
Наявність обмежень визначає два типи задач оптимізації:
1) досягнення заданого рівня критерію ефективності при мінімальній витраті ресурсів;
2) досягнення максимального рівня критерію ефективності при повній витраті виділених для досягнення мети ресурсів.
Типовим прикладом задач першого типу є добір складу заданої марки бетону при мінімальній витраті цементу. Типова задача другого типу - досягнення заводом максимального випуску бетону при визначених запасах цементу. До критеріїв ефективності, призначених для технологічних рішень, пред'являється ряд вимог:
1) критерій повинний характеризувати ефективність технології з урахуванням кінцевої мети виробництва, а не окремих його етапів, проте у складних системах при використанні східчастій оптимізації припускається застосування різних критеріїв на кожному етапі;
2) критерій повинний бути кількісним і однозначним, причому бажано, щоб він мав фізичний зміст і легко обчислювався (якщо у критерія немає числової оцінки, то, як виняток, припустимо застосування рангів: 1, 2,..., п по деяких формалізованих шкалах;
3) критерій повинний мати статистичну ефективність, що характеризується нечутливістю критерію до малих випадкових впливів і мінімальної (у границях метрологічної точності) помилкою відновлюваності для рівнобіжних дослідів в одній серії;
4) критерій по можливості повинний мати універсальність, тобто враховувати й економічну, і технічну сторони технології (у цьому змісті відносна міцність бетону на одиницю витрати цементу - більш універсальний критерій, чим абсолютна міцність бетону). Правильний вибір критерію ефективності - необхідна умова успішного прийняття оптимального рішення.
Керування системою припускає прийняття обґрунтованих рішень про той або інший вибір або зміну вхідних параметрів (технологічних чинників стосовно до виробництва бетону). Вибір правильного рішення з великого числа варіантів значно полегшується при формалізації процесу ухвалення рішення й застосуванні кількісного опису альтернатив. При цьому швидкий аналіз системи в необхідному випадку забезпечує використання ЕОМ, у програму якої закладена математична модель поведінки системи.
Модель - особлива форма абстрагування, тобто відволікання тих або інших елементів і зв'язків від множини реально існуючих у системі. Поза залежністю від методів аналізу, що залучаються до рішення задачі (фізики, хімії, кібернетики і т.п.) виникає необхідність побудови деяких абстракцій. У залежності від того, які сторони об'єкта подані в моделі, розрізняють моделі: 1) субстанційні; 2) структурні; 3) функціональні.
Матеріал субстанційних моделей (речовина, субстанція) по своїх деяких властивостях збігається з матеріалом оригіналу. Наприклад, контрольний зразок-куб бетону, виготовлений паралельно з конструкцією, є субстанційною моделлю її матеріалу, тому що бетон у зразку по своїх основних властивостях збігається з бетоном конструкції.
Під структурною моделлю розуміється модель, що імітує внутрішню структуру оригіналу (засіб організації елементів об'єкта). При цьому може моделюватися як структура процесу, наприклад, технологічна система виробництва бетону, так і статистична структура, наприклад, засоби укладки зерен заповнювача різноманітних фракцій у масі бетону
Функціональні моделі імітують засіб поведінки (функцію) оригіналу. Функціональний підхід, роль якого в сучасній науці різко зросла, характеризується як би подвійною абстракцією - абстрагуванням спочатку від речовинного субстрату системи з обчисленням її внутрішньої структури і наступного абстрагування від останньої з виділенням функціональних зв'язків системи із середовищем. Узагальненою абстрактною уявою функціональної моделі взагалі є метод «чорного ящика», що одержав у кібернетику широке поширення і теоретичну розробку. Поняття «чорний ящик» описує таку систему, внутрішня структура якої невідома і не доступна для спостереження, а відомі лише параметри “входу” - Хі (фактори) і «виходу» Y (критерій ефективності J, відгук і т.д.). У цьому випадку задача керування зводиться до добору таких рівнів Х, що забезпечили б визначені значення Y, зокрема оптимальні. Досліджуючи значення Х і відповідні їм значення Y, можна знайти статистичну закономірність, що описує цей зв'язок.
Такий підхід до задач технології бетону дозволяє абстрагуватися від деяких складних і поки мало вивчених фізико-хімічних явищ, що відбуваються в бетонах у процесі їхнього одержання й експлуатації. Проте це не заперечить необхідності подальших досліджень причин і явищ у структурі системи, тому що чим повніше наші уявлення про процес або явище, тим точніше й достовірніше математичні моделі, які їх відбивають. Метод «чорного ящика», засновано на використанні емпіричних методів при системному кібернетичному підході, дозволяє знайти й використовувати в керуванні технологією статистичні закономірності.
У результаті кількісного дослідження функціональної моделі «чорного ящика» вдасться одержати сукупність співвідношень, що виражають у виді математичних залежностей (графіків, рівнянь, нерівностей, логічних умов, графів і т. д) реальні фізичні характеристики систем. Ця сукупність співвідношень разом з умовами, що обмежують границі зміни фізичних характеристик, дозволяє побудувати математичну модель. Іншими словами, математичною моделлю називається опис системи на формальній мові, що дозволяє виводити судження про деякі риси поведінки цієї системи за допомогою формальних процедур над її описом. У залежності від використаних систем одержують моделі, що узагальнюють, із відомою точністю, визначений процес або явища, як, наприклад, узагальнені моделі міцності бетону (типу формули міцності бетону, яку запропоновано Боломєм, з усередненими коефіцієнтами, отриманими за результатами випробувань бетону на різних матеріалах), або окремі моделі, що описують даний процес або явище в конкретних умовах, наприклад модель міцності бетону (графік або формула) для визначених видів матеріалів, використовуваних на даному об'єкті будівництва.
Найбільшу складність при побудові будь-якої математичної моделі представляє рішення питання про вибір форми зв'язку між перемінними. Проте ряд труднощів моделювання можна виключити, якщо прийняти обмеження: модель повинна, як можна точніше описувати поведінку системи в конкретній ситуації. Тоді можна виходити з принципу максимальної початкової простоти моделі поведінки, а не шукати в кожній задачі спеціальних математичних форм зв'язку між факторами Х (число факторів k) і відгуком Y. Якщо найпростіша модель виявиться недостатньо точною, її можна ускладнити. Скориставшись тим, що будь-яку безупинну функцію можна розкласти в ряд Тейлора, що перетвориться у статечний ряд, початкову модель поведінки системи зручно уявити у виді поліному m-того ступеня (на практиці достатньо т <З)
 (24.1)
(24.1)
При розрахунку за результатами дослідження системи необхідно як можна точніше знайти оцінки bі →βі і т. п. у такій локально-інтегральній моделі. Це дозволяє для щирого значення уп одержати по моделі (24.1) розрахункову величину у
 (24.2)
(24.2)
Коефіцієнти bi моделі (24.2) визначають методом найменших квадратів.
Для визначення залежності у необхідно мати хоча б два різноманітних значень xi. При k - факторній поліномінальній моделі потрібно не менше  різноманітних спостережень. Використання локально-інтегрального (поліномінального) моделювання - це один з окремих, хоча і дуже поширених методів побудови моделі технологічної ситуації.
різноманітних спостережень. Використання локально-інтегрального (поліномінального) моделювання - це один з окремих, хоча і дуже поширених методів побудови моделі технологічної ситуації.
У технології бетону можна використовувати різноманітні математичні методи, що умовно можна розділити на три групи:
група А - ймовірносно-статистичні методи, що включають використання загальної теорії ймовірності, описової статистики, вибіркового методу й перевірку статистичних гіпотез, дисперсійного й регресивного аналізу, математичної теорії експериментів і ін.;
група Б - методи дослідження операцій, що включають лінійне, нелінійне й динамічне програмування теорію ігор, теорію масового обслуговування, теорію графів і мереж і т.д.
група В - методи математичного аналізу, що включають диференціальне, інтегральне й векторне числення, диференціальні рівняння, у тому числі рівняння математичної фізики, використовувані для упорядкування й розрахунку математичних моделей на основі визначених передумов про фізико-хімію досліджуваних процесів.
Таке виділення груп умовно, оскільки побудовані статистичними методами математичні моделі можуть вивчатися надалі за допомогою, наприклад, лінійного програмування.
Математичне моделювання повинно проводитися тільки на основі інформації про конкретну технологічну ситуацію. Для детермінованих моделей необхідно, як правило, уявлення про їхню фізико-хімічну природу й залежності, що управляють процесом, який спостерігається. При побудові статистичних моделей можна обмежитися зведеннями про те, як зміна технологічних чинників х впливає на кінцеву якість у. Ці відомості можна одержати тільки спостереженням за обраною системою, причому поняття «спостереження» тут варто трактувати широко як власне спостереження і як експеримент.
При власному спостереженні дослідник - лише пасивний свідок явищ, що відбуваються, а самий процес спостережень ніяк не впливає на розвиток цих явищ. Модель, побудована на основі такого спостереження, буде справедлива тільки для діапазону зміни чинників, що спостерігався, а умови оптимальності можуть мати окремий характер і можуть не збігатися з положенням головного оптимуму
Більш високий ступінь пізнання системи забезпечує експеримент, при якому досліджувані процеси виконуються в необхідних умовах. Експеримент дозволяє побудувати більш досконалі моделі, чим моделі, отримані в результаті тільки спостереження.
Роздивимося модель, що часто використовують для рішення технологічних задач. Для простоти викладу приймемо лише три параметри входу: Х1, Х2, Хз і один параметр виходу у, хоча усе далі сказане про цю модель легко узагальнюється на k-мірну модель. Система є стохастичною, оскільки на неї крім контрольованих і регульованих факторів xi діють випадкові чинники, для яких заздалегідь невідомі ні кількісні, ні якісні оцінки.
Для вивчення цієї технологічної системи можуть бути обрані два шляхи збору інформації: спостереження й експеримент. Інформація про поведінку системи представляє у виді табл. 24.1.
Таблиця 24.1.
Результати вимірів у трифакторної ситуації
| Номер досліду | Значення факторів | Число паралельних вимірювань | Вихід | ||
| Х1 | Х2 | Х3 | |||
 1 1
| x11 | x21 | x31 | m1 | y1 |
| x21 | x22 | x32 | m2 | y2 | |
| ... | … | … | … | … | … |
| u | xu1 | xu2 | xu3 | mu | yu |
| … | … | … | … | … | … |
| N | x1N | x2N | x3N | mN | yN |
Спостереження звичайно ведеться у виробничих умовах, коли не можна змінювати в будь-яких границях значення х через ризик розбудувати нормальний технологічний процес і припустити брак у продукції. Через визначені проміжки часу (рідше безупинно) фіксують значення входу xi і виходу yі. При спостереженні за системою рівні вхідних факторів xi виявляються розташованими безсистемно, хаотично, тому що спостерігач не регулює їх за своїм розсудом.
При проведенні попередніх експериментів фактори, що варіюються, змінюються свідомо по спеціальному плані і фіксуються значення виходу, що відповідають тієї або іншої заздалегідь наміченої комбінації х. У табл. 24.1 виділене поле, що обмежує число дослідів N, рівні чинників хі, число рівнобіжних вимірів т. Це поле називають «планом експерименту»; дійсно при проведенні попередніх дослідів завжди намічають проведення того або іншого числа дослідів із визначеною кількістю повторень, змін факторів. Упорядкування плану доцільно проводити на основі математичної теорії експерименту, що вивчає оптимальне керування експериментом при неповному знанні механізму явища.
Спланувати експеримент для вивчення системи аналізованої моделі - це, зокрема, означає:
а) вибрати ті фактори Х1, Х2, Хз, рівні яких технолог збирається змінювати;
б) намітити границі їхнього варіювання [Xі]max і [Xі]min;
в) намітити комбінацію рівнів факторів Хi, при якому буде досліджуватися система, або розмістити координати Х1, Х2, Хз дослідних точок у факторному просторі. При цьому розрізняють два принципи постановки експерименту: пасивний і активний.
При пасивному експерименті розташування точок у факторному просторі ведеться на інтуїтивному рівні без урахування методів подальшого математичного опрацювання інформації. Частіше усього пасивний експеримент застосовують при варіюванні одного-двох факторів і сталості інших.
Інформація, зібрана при активному експерименті по математично обґрунтованому плані, що враховує мету експерименту й методи опрацювання його результатів, має велику цінність, чим інформація від пасивного експерименту. При цьому практично завжди менше витрати ресурсів (матеріальних і тимчасових) на активний експеримент, тому що скорочується кількість виконуваних досвідів. Виділив простір, у границях якого змінюються вхідні параметри, кодують чинники, тобто переносять початок координат у центр простору і відносять їхню величину до ширини інтервалу варіювання. Така операція забезпечує отримання чинників без розмірів і різко спрощує обчислювальну роботу. Планування експерименту істотно полегшує дослідження стохастичних технологічних систем і одержання точних і достовірних математичних моделей.
Застосування математичних моделей, що одержують у результаті попередніх дослідів і в яких можна враховувати велику кількість факторів, що діють у конкретних умовах виробництва, дозволяє не тільки уточнити технологічні розрахунки, але й успішно управляти якістю бетону і його виробництвом, вносячи необхідні корективи у процес при будь-якій зміні вхідних параметрів. Математичні моделі одержують у результаті правильно спланованого експерименту і застосовують у тих конкретних умовах, для яких вони отримані. Для інших умов потрібно перевіряти придатність тієї або іншої моделі і вносити відповідні корективи.
Процес одержання багатофакторних математичних моделей включає такі етапи: розрахунок величині основного вихідного технологічного показника; вибір факторів і інтервалів їхнього варіювання; вибір плану й умов проведення експериментів; розрахунок усіх можливих величин даного технологічного чинника й проведення експериментів по обраному плані; опрацювання результатів експериментів з одержанням математичних залежностей властивостей бетону і бетонної суміші від обраних чинників.
У якості факторів (величин, що варіюються в експериментах) у залежності від умов задачі можуть прийматися режими виконання технологічних операцій і т.п.
При проведенні дослідів усі фактори варіюють тільки на двох рівнях - верхньому й нижньому, віддалених від основного рівня у більшу й меншу сторони на однакову величину, називану - інтервал варіювання. Інтервал варіювання встановлюють у залежності від границь раціонального коливання факторів.
Для спрощення записів і наступних розрахунків верхній рівень факторів позначається символом (+1), а нижній рівень - символом (-1). Такий запис, однаковий з перекладом факторів у новий кодовий масштаб по формулі
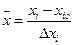 (24.3)
(24.3)
де 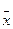 - значення і-ro фактора в новому, кодовому масштабі;
- значення і-ro фактора в новому, кодовому масштабі;
хі - значення і-го фактора у старому натуральному масштабі;
xіо - основний рівень і-ro фактора;
Δхі - інтервал варіювання і-ro фактора.
Експерименти в залежності від кількості факторів виконують за спеціальним планом. Приклад плану для трифакторного експерименту приведено в табл. 24.2. Аналогічним способом складають таблиці і при іншому числі факторів.
Таблиця 24.2
План проведення експериментів при числі факторів,
яке дорівнює 3
| № досліду | Матриця планування | Властивість бетону уі | |||||
| х1 | х2 | х3 | х12 | х13 | х23 | ||
| -1 | -1 | +1 | +1 | -1 | -1 | ||
| -1 | -1 | +1 | |||||
| -1 | -1 | -1 | +1 | +1 | +1 | ||
| -1 | +1 | +1 | -1 | -1 | +1 | ||
| -1 | +1 | -1 | |||||
| -1 | +1 | -1 | -1 | +1 | -1 | ||
| -1 | +1 | -1 | |||||
| -1 | |||||||
| -1 | -1 | +1 | |||||
| +1 | -1 | +1 | -1 | +1 | -1 | ||
| +1 | -1 | -1 | |||||
| +1 | -1 | -1 | -1 | -1 | +1 | ||
| +1 | +1 | +1 | +1 | +1 | +1 | ||
| +1 | +1 | +1 | |||||
| +1 | +1 | -1 | +1 | -1 | -1 | ||
| +1 | +1 | +1 | |||||
| +1 | |||||||
| +1 | -1 | -1 | |||||
| -1 | +1 | -1 | |||||
| -1 | |||||||
| -1 | -1 | +1 | |||||
| +1 | +1 | +1 | |||||
| +1 | |||||||
| +1 | -1 | -1 | |||||
| +1 | |||||||
| -1 |
У гр. 1 табл. 24.2 задається порядок виконання дослідів. У гр. 2-4 поміщені значення відповідно першого (Xi), другого (Х2) і третього (Х3) факторів. Ці графи задають умови проведення дослідів. Так, відповідно до плану, у першому досліді фактори X1= -1 і Х2= -1 повинні встановлюватися на нижньому рівні, а фактор X3= +1 - на верхньому.
Значення гр. 5-7 (х1х2, х1х3, х2х3) отримані шляхом перемноження елементів гр. 2-4. Якщо значення гр. 2- 4 застосовуються для визначення умов дослідів, то значення гр. 5-7 використовуються для опрацювання їхніх результатів. У наступних графах таблиці поміщають результати визначень властивостей бетону.
Після проведення дослідів у послідовності, яку зазначено планом (гр. 1 табл. 24.2), їх повторюють у зворотній послідовності, одержуючи, таким чином, за двома спостереженнями (результатами) у кожному досліді.
Обсяг бетону в кожному досліді встановлюють з урахуванням числа обумовлених характеристик бетону (міцність на стиск, розтяг, вигин і т.д.). Готування бетонної суміші, формування зразків, випробування бетонної суміші і затверділого бетону, обчислення фактичних витрат матеріалу виконують у звичайному порядку.
Результати дослідів опрацьовують методами математичної статистики, одержуючи при цьому в алгебраїчній формі рівняння, що виражають залежності досліджуваних властивостей бетону від вихідних факторів, наприклад, для двофакторного експерименту

де і = l, 2 - порядкові номера факторів,
у - властивість бетону, що досліджується
хі - вхідні фактори,
bі - коефіцієнти.
Після одержання рівнянь виконують перевірку відмінності коефіцієнтів bі від нуля й придатності рівнянь для опису досліджуваних залежностей.
Дані перевірки виконують по критеріях Стьюдента й Фішера. У кожному досліді обчисляють абсолютне значення різниці між двома рівнобіжними спостереженнями по формулі lu = |y1u - y2u| визначають середнє квадратичне відхилення, що характеризує помилку досліду, по формулі

і обчисляють довірчий інтервал для коефіцієнтів рівнянні по формулі
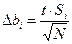 (24.4)
(24.4)
де t - значення критерію Стьюдента, прийняте по табл. 24.3 у залежності від числа ступенів свободи fi, з яким визначалося Si.
При дворазовому повторенні кожного досліду число ступенів свободи дорівнює числу дослідів N, тобто fi = N.
Таблиця 24.3
Значення критерію Стьюдента t для 5 %-ного рівня значимості
| Число ступенів свободи | |||||||||
| Критерій Стьюдента | 2,78 | 2,31 | 2,23 | 2,18 | 2,15 | 2.12 | 2,09 | 2.06 | 2,04 |
Абсолютні значення коефіцієнтів рівняння порівнюють із довірчим інтервалом, обчисленим по формулі (24.4). Якщо абсолютне значення коефіцієнта перевищує довірчий інтервал, його визнають значимим, у противному випадку коефіцієнт і відповідний йому член рівняння відкидають. Отримане після цієї процедури уточнене рівняння містить тільки члени зі значимими коефіцієнтами. Для перевірки придатності отриманого уточненого - рівняння обчисляють дисперсію по формулі

де уu - середнє значення досліджуваної властивості бетону в u-му
досліді,
уиp - значення досліджуваної властивості бетону в u-му досвіді,
обчислене по уточненому рівнянню;
k - кількість коефіцієнтів, включаючи bo, у рівнянні після
відкидання незначущих коефіцієнтів (прирівняних до нуля).
Емпіричне значення Fе-критерію визначають по формулі

та порівнюють із табличним значенням F-критерію (табл. 24.5) для ступенів свободи, з якими визначалися  та
та  . Число ступенів свободи, що відповідає
. Число ступенів свободи, що відповідає  , обчисляють по формулі f2 = N - k.
, обчисляють по формулі f2 = N - k.
Таблиця 24.5
Значення F- критерію для 5 %-ного рівня значимості
| f2 | F-критерій при f1 | f2 | F-критерій при f1 | ||||
| 7,71 | 5.32 | 4,49 | 8 | 6,04 | 3,44 | 2.59 | |
| 6,94 | 4.46 | 3,63 | 6.00 | 3,39 | 2.54 | ||
| 6,59 | 4,07 | 3,24 | 5.96 | 3,35 | 2,49 | ||
| 6,39 | 3,84 | 3.01 | 5,91 | 3,28 | 2,42 | ||
| 6.26 | 3,69 | 2,85 | 5,86 | 3,22 | 2,35 | ||
| 6.16 | 3,58 | 2,74 | 5,80 | 3,15 | 2,28 | ||
| 6,09 | 3,50 | 2,66 |
Рівняння признається придатним, якщо Fе<F. Перед тим, як використовувати отримане рівняння для рішення поставлених задач, необхідно перевірити його у виробничих умовах.
Планування експериментів може проводитися і по інших планах, приклади яких приводяться у спеціальній літературі.
Питання для самоконтролю
1. Класи систем
2. Що таке детерміновані системи
3. Що таке стохастичні системи
4.Як визначають ефективність технологічного процесу
5. Задачі оптимізації
6. Вимоги до критеріїв ефективності технологічних процесів
7. Що таке модеь
8. Які бувають моделі
9.Що таке субстанційна модель
10. Що таке структурна модель
11. Що таке функціональна модель
12. Математичні методи, які можна використовувати у
технології бетону
13. Що таке “план експерименту” і як він розробляється
14. Процес одержання багатофакторних математичних
моделей
15. Як виконують перевірку відмінності коефіцієнтів b від
нуля й придатності рівнянь для опису досліджуваних
залежностей.
16. Коли рівняння математичної моделі визнають придатним
до використання.
Читайте також:
- D і 3D технології креслення в AutoCAD
- OLAP-Технології
- PR-ІНСТРУМЕНТАРІЙ І МАНІПУЛЯТИВНІ ТЕХНОЛОГІЇ
- PR-технології у виборчій кампанії.
- PR-технології.
- Web-технології
- Бетонування в зимових умовах
- Варіантне проектування технології зведення будівель та споруд.
- Вартість Internetу для підприємств-користувачів. Internet-технології та формування бізнес-фокусу споживача.
- Виборчі технології як найважливіша складова ПР
- Визначення розташування арматури і товщини захисного шару бетону
- Використання в логістиці технології автоматизованої ідентифікації штрихових кодів
| <== попередня сторінка | | | наступна сторінка ==> |
| УМОВИ ПРОВЕДЕННЯ ВИПРОБУВАННЯ. | | | Загальні положення |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |