• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Недетерміновані скінченні автомати

Визначення 2.1.1. Скінченний автомат (finite automaton, finite-state machine) - це п’ятірка , де - скінченний вхідний алфавіт (або просто алфавіт) даного скінченного автомату, Q і - скінченні множини,

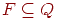, . Елементи Q називаються станами (state), елементи I - початковими (initial) станами, елементи F - заключними або допускаючими (final, accepting) станами. Якщ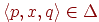о , то 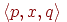називається переходом (transition) з p в q, а слово x - міткою (label) цього переходу.

Приклад 2.1.2. Нехай Q = {1,2}, , I = {1}, F = {2},

Тоді 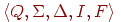- скінченний автомат.

Зауваження 2.1.3. Скінченні автомати можна зображати у вигляді діаграм станів (state diagram) (іноді їх називають діаграмами переходів (transition diagram)). На діаграмі кожний стан позначається кружком, а перехід - стрілкою. Стрілка з p в q, помічена словом x, показує, що 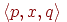являється переходом даного скінченного автомату. Кожний початковий стан розпізнається по вхідній в нього короткій стрілці. Кожний допускаючий стан відмічається на діаграмі подвійним кружком.

Приклад 2.1.4. На діаграмі зображено скінченний автомат з прикладу 2.1.2.

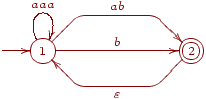
Зауваження 2.1.5. Якщо в скінченому автоматі є декілька переходів з спільним початком і спільним кінцем, то такі переходи називаються паралельними. Іноді на діаграмі станів скінченого автомату паралельні переходи зображаються одною стрілкою. При цьому мітки переходів перераховують через кому.

Приклад 2.1.6. На діаграмі зображено скінченний автомат з прикладу 2.1.2.

Визначення 2.1.7. Шлях (path) скінченого автомату - це кортеж , де і для кожного i. При цьому q₀ – початок шляху q_n - кінець шляху n - довжина шляху w₁...w_n - мітка шляху.

Зауваження 2.1.8. Для любого стану існує шлях 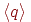. Його мітка - 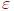, початок і кінець співпадають.

Визначення 2.1.9. Шлях називається успішним якщо його початок належить I, а кінець належить F.

Приклад 2.1.10. Розглянемо скінченний автомат з прикладу 2.1.2. Шлях 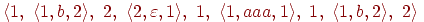являється успішним. Його мітка - baaab. Довжина цього шляху - 4.

Визначення 2.1.11. Слово w допускається (is accepted, is recognized) скінченим автоматом M, якщо воно являється міткою деякого успішного шляху.

Визначення 2.1.12. Мова, що розпізнається скінченим автоматом M, - це мова L(M), яка складається з міток усіх успішних шляхів (тобто з усіх слів, що допускаються даним автоматом ). Будемо також говорити, що автомат M распізнає (recognizes, accepts) мову L(M).

Зауваження 2.1.13. Якщо , то мова, що розпізнається скінченим автоматом 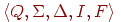, містить .

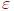Приклад 2.1.14. Нехай , де Q = {1,2}, , I = {1}, F = {1,2},

Тоді

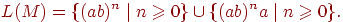
Визначення 2.1.15. Два скінченних автомати еквівалентні, якщо вони розпізнають одну і ту ж мову.

Визначення 2.1.16. Мова L називається автоматною (finite-state language), якщо існує скінченний автомат, що розпізнає цю мову.

Зауваження 2.1.17. Переважно в підручниках використовують більш вузьке визначення недетермінованого скінченого автомату, але це не змінює класу автоматних мов (див. лему 2.3.3.).

Приклад 2.1.18. Розглянемо однобуквений алфавіт 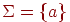. При любих фіксованих 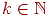і мова 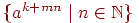являється автоматною.

Зауваження 2.1.19. Кожна скінченна мова являється автоматною.

Визначення 2.1.20. Стан q досягається (reachable) з стану p, якщо існує шлях, початком якого являється p, а кінцем - q.

Лемма 2.1.21. Кожна автоматна мова розпізнається деяким скінченим автоматом, в якому кожний стан досягається з деякого початкового стану і з кожного стану досягається хоча б один заключний стан.

Приклад 2.1.22. Розглянемо скінченний автомат 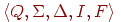, де Q = {1,2,3,4}, 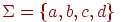, I = {1,2,4}, F = {1,3,4},

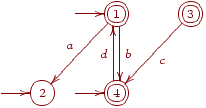
Видалимо ті стани (і переходи в яких ці стани використовуються), які не задовільняють вимогам леми 2.1.21. Отримуємо еквівалентний скінченний автомат 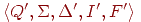, де Q' = {1,4}, I' = {1,4}, F' = {1,4},

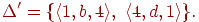
Зауваження 2.1.23 Природнім узагальненням скінченного автомату являється скінченний перетворювач (finite-state transducer), який дозволяє на кажному такті відправити декілька символів в додатковий "вихідний" потік. В деяких книгах скінченними автоматами називають саме такі пристрої (з вихідним потоком).

В даному посібнику скінченні перетворювачі розглядатися не будуть.

Вправа 2.1.24. Знайти скінченний автомат, який розпізнає мову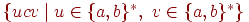

Вправа 2.1.25. Знайти скінченний автомат, який розпізнає мову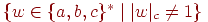

Вправа 2.1.26. Знайти скінченний автомат, який розпізнає мову

Вправа 2.1.27. Знайти скінченний автомат, який розпізнає мову

Вправа 2.1.28. Знайти скінченний автомат, який розпізнає мову

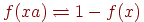Вправа 2.1.28. Знайти скінченний автомат, який розпізнає мову , де , і 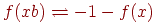для любого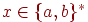

Читайте також:

1. Active-HDL як сучасна система автоматизованого проектування ВІС.
2. Автомати для комбінованої торгівлі
3. Автомати для продажу гарячих напоїв
4. Автомати для продажу гарячих страв
5. Автомати для продажу штучних товарів
6. Автоматизація банківської діяльності в Україні
7. Автоматизація вводу
8. Автоматизація виробництва
9. Автоматизація виробничих процесів
10. Автоматизація водорозподілу з комбінованим регулюванням
11. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
12. Автоматизація водорозподілу регулювання зі сталими перепадами

Переглядів: 1751