• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Операційні залежності

Основні результати операційного аналізу формуються у вигляді співвідношень між операційними змінними. Ці співвідношення ґрунтуються на гіпотезі про баланс потоків у мережі: кількість вимог, що надійшли до деякого вузла протягом тривалого періоду часу Т, дорівнює кількості вимог, які залишили цей вузол. Ця гіпотеза визначає умови роботи мережі СМО в сталому режимі, тобто вважається, що вимоги завжди залишають вузли мережі, або розглядається досить довгий період часу Т. Баланс потоків вимог існує тільки для деякого періоду спостереження за системою, але це дуже непогане наближення у разі тривалого періоду часу Т, тому що відношення (A_k – C_k)/C_k зазвичай незначне.

Гіпотеза про баланс дає змогу визначати залежність між операційними змінними для кожного вузла мережі, а також записати рівняння балансу потоків вимог:

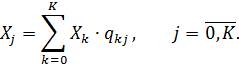
(2.11)

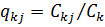Справедливість виразу (2.11) випливає з припущення про баланс потоків вимог у мережі, тобто A_j = C_j, бо але за умови, що , знаходимо 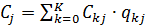. Поділивши останнє співвідношення (ліву та праву його частини) на загальний час спостереження Т, отримаємо вираз (2.11). Рівняння (2.11) буде мати єдиний розв'язок для замкненої мережі у разі заданого значення Х₀. Для розімкненої мережі рівняння (2.11) будуть лінійнозалежними, однак і в цьому випадку вони дають корисну інформацію про динаміку потоків мережі.

За допомогою виразу (2.10) знаходимо продуктивність вузла, тобто інтенсивність, з якою вимоги залишають вузол k:

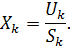
Визначаємо коефіцієнт відвідування вузла k вимогами:

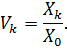
(2.12)

Рівняння балансу потоку можна записати як еквівалентну систему рівнянь, в якій замість інтенсивності потоків використовуються коефіцієнти відвідування кожного вузла мережі.

Поділимо ліву і праву частини виразу (2.11) на X₀:

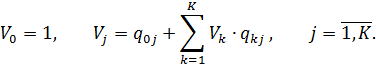
(2.13)

Вираз (2.13) справедливий, якщо справедливе рівняння (2.11).

Зв'язок коефіцієнтів відвідування та продуктивності вузла визначаємо за формулою

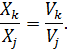
Обчислимо середній час R перебування вимог у стохастичній мережі. Позначимо час перебування вимог у окремих вузлах через R_k. Введемо ще одну операційну змінну W_k, яка дорівнює сумарному часу чекання та часу обслуговування вимог у вузлі k протягом часу Т:

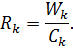
(2.14)

Середній час перебування вимог у системі R можна знайти через R_k і коефіцієнти відвідування окремих вузлів вимогами, тобто

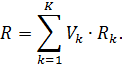
(2.15)

Це загальний закон часу перебування, який справедливий і в тому випадку, коли гіпотеза про баланс потоків не виконується.

Знайдемо середню кількість вимог у мережі N, яка визначається через середню кількість вимог у кожному вузлі n_k,

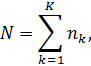
де n_k — операційна змінна, яку можна отримати з основних операційних змінних:

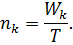
(2.16)

Для середнього часу перебування вимог у мережі справедливий закон Литтла, тобто середній час перебування вимог у k-му вузлі визначається через середню кількість вимог у ньому та інтенсивність потоку:

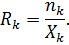
(2.17)

Обґрунтувати формулу Литтла можна також із застосуванням операційного аналізу.

З виразу (2.16) знаходимо

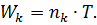
Підставляємо отриману операційну змінну в рівняння (2.14):

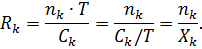
Закон Литтла справедливий також для всієї мережі в цілому. Підставивши формули (2.12) і (2.17) у вираз (2.15), отримаємо

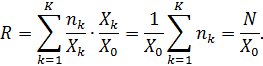
(2.18)

Покажемо, як можна використовувати основні співвідношення операційного аналізу для визначення часу перебування вимог у замкненій мережі (рис. 2.18).

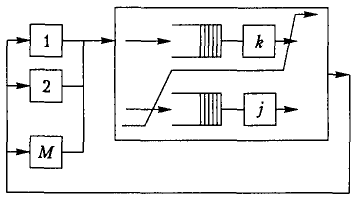
Рис. 2.18. Замкнена мережа СМО

Нехай є М пристроїв, час обслуговування вимоги кожним із них — Z. Середній час перебування вимоги в мережі визначаємо за формулою

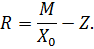
(2.19)

Вираз (2.19) випливає з таких міркувань. Середній час одного циклу взаємодії, який включає час обслуговування вимоги в зовнішній мережі та перебування в одному з М пристроїв, визначається сумою (Z + R). Якщо припустити, що виконується гіпотеза про баланс потоків, то для заданого циклу справедлива формула Литтла. Тому величина М = (Z + R)´X₀ має визначати середню кількість зайнятих пристроїв або середню кількість працюючих пристроїв для системи з відмовами.

Продемонструємо використання наведених співвідношень операційного аналізу на прикладах. Зображені в них моделі мереж стосуються моделювання обчислювальних систем, але зазначені розрахунки мають загальний характер і демонструють можливості операційного аналізу.

Читайте також:

1. Аверсивную терапію використовують, як правило, при лікуванні алкоголізму, нікотиновій залежності і деяких інших захворювань.
2. Аналіз фінансової незалежності підприємства
3. Аспекти незалежності аудиторської професії
4. Аспекти незалежності аудиторської професії.
5. В залежності від джерел сплати
6. В залежності від мети та характеру угоди, які лежать в основі випуску векселів, а також їх забезпечення розрізняють комерційні, фінансові та фіктивні векселя.
7. В залежності від обстановки та бойового завдання, наявності сил та засобів, а також від характеру місцевості, оборона може бути позиційною, маневреною .
8. В залежності від обстановки та бойового завдання, наявності сил та засобів, а також від характеру місцевості, оборона може бути позиційною, маневреною .
9. В залежності від підстав укладеннядоговори поділяються на вільні та обов'язкові.
10. В залежності від того, хто може вимагати виконання договору,останні поділяються на договори, що укладаються на користь їх учасників, та договори на користь третьої особи.
11. ВИДИ НАВІЮВАНЬ В ЗАЛЕЖНОСТІ ВІД ЇХ ВМІСТУ
12. Види травм в залежності від шкідливих та небезпечних виробничих факторів .

Переглядів: 705