• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Геометричний і структурний підходи

Будь-яке зображення, яке виникає в результаті|внаслідок| спостереження якого-небудь об'єкту в процесі навчання|навчання| або іспиту|екзамена|, можна представити|уявляти| у вигляді вектора, а значить і у вигляді точки деякого простору|простір-час| ознак. Якщо стверджується, що при показі зображень можливо однозначно віднести їх до одного з двох (або декілька) образів|зображень|, то тим самим стверджується, що в деякому просторі|простір-час| існує дві (або декілька) області, що не мають загальних|спільних| точок|точок|, і що зображення – точки|точки| з|із| цих областей. Кожній такій області можна дати назву, відповідну образу|зображенню|.

Якщо зображення, що пред'являються, належать не двом, а більшому числу образів|зображень|, то задачі|задача| полягає в побудові|шикуванні| по показаних в ході навчання|навчання| точках|точках| поверхні, що розділяє всі області, відповідні цим образам|зображенням|, один від одного. Такого роду задачі можуть бути вирішені, наприклад, шляхом побудови|шикування| функції, що приймає над крапками|точками| кожній з областей однакове значення, а над крапками|точками| з|із| різних областей значення цієї функції має бути різне.

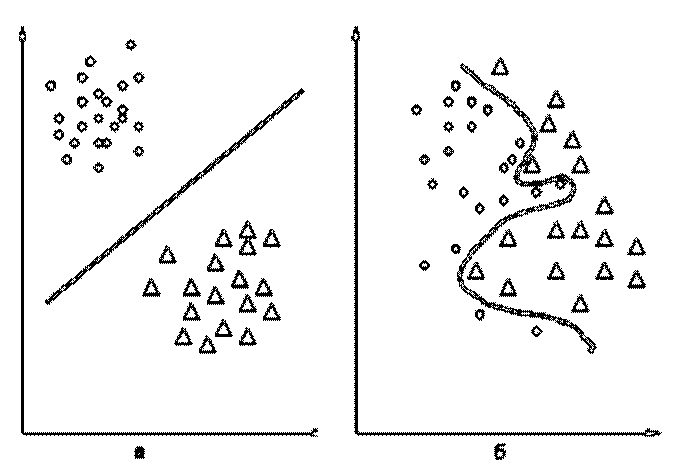
Рис. 2 - Два образи|зображення|.

На перший погляд здається|видається|, що знання всього лише|усього лише| деякої кількості точок|точок| з|із| області є недостатнім, аби|щоб| відокремити|відділити| всю область. Дійсно, можна вказати незліченну кількість різних областей, які містять|утримують| ці точки|точки|, і як би не була побудована|спорудити| по ним поверхня, що виділяє область, завжди можна вказати іншу область, яка пересікає|перетинає| поверхню і в той же час|разом з тим| містить|утримує| показані точки|точки|. Проте|однак| відомо, що задачі|задача| про наближення функції за інформацією про неї в обмеженій множині точок|точок| є істотно|суттєвий| вужчою, ніж вся множина|множина|, на якій функція задана, є звичайним|звичним| математичним задачею|задачею| про апроксимацію функцій. Зрозуміло, вирішення таких завдань|задач| вимагає введення|вступу| певних обмежень на класи даних функцій, а вибір цих обмежень залежить від характеру інформації, яку може додати|добавляти| вчитель|учитель| в процесі навчання|навчання|. Однією з таких підказок є гіпотеза про компактність образів|зображень|. Інтуїтивно ясно, що апроксимація розділяючої функції буде задачею|задачею| тим більше легкою, ніж компактніші і ніж більш рознесені в просторі|простір-час| області, що підлягають розділенню|поділу|. Так, наприклад, у випадку, показаному на Рис. 2а|, розділення|поділ| свідомо простіше, ніж у випадку, показаному на Рис. 2б|. Дійсно, у випадку, представленому|зображати| на Рис. 2а|, області можуть бути розділені площиною, і навіть при великих погрішностях у визначенні розділяючої функції вона все ж |все же таки|продовжуватиме розділяти області. У випадку ж на Рис. 2б|, розділення|поділ| здійснюється хитромудрою поверхнею і навіть незначні відхилення в її формі наводять|приводять| до помилок розділення|поділу|. Саме це інтуїтивне уявлення про порівняно легко роздільних областях привело до гіпотези компактності.

Разом з|поряд з| геометричною інтерпретацією проблеми навчання|навчання| розпізнаванню образів|зображень| існує і інший підхід, який називають структурним, або лінгвістичним. Пояснимо лінгвістичний підхід на прикладі|зразку| розпізнавання зорових зображень. Спочатку виділяється набір вихідних|початкових| понять – типових фрагментів, що зустрічаються на зображеннях, і характеристик взаємного розташування фрагментів – "зліва|ліворуч|", "знизу", "всередині|всередині|" і так далі. Ці вихідні|початкові| поняття утворюють словник, що дозволяє будувати різні логічні вислови|висловлювання|, інколи|іноді| їх називають припущеннями. Задача|задача| полягає в тому, аби|щоб| з|із| великої кількості висловів|висловлювань|, які могли б бути побудовані|спорудити| з використанням цих понять, відібрати найбільш істотні|суттєві| для даного конкретного випадку.

Далі, переглядаючи|проглядати| кінцеве|скінченне| і по можливості невелике число об'єктів з|із| кожного образу|зображення|, потрібно побудувати|спорудити| опис цих образів|зображень|. Побудовані|спорудити| описи мають бути настільки|так| повними|цілковитими|, аби|щоб| вирішити питання про те, до якого образу|зображення| належить даний об'єкт. При реалізації лінгвістичного підходу виникають дві задачі|задачі|: задачі|задача| побудови|шикування| вихідного|початкового| словника, тобто набір типових фрагментів, і задачі|задача| побудови|шикування| правил опису з|із| елементів заданого словника.

В рамках|у рамках| лінгвістичної інтерпретації проводиться аналогія між структурою зображень і синтаксисом мови|язика|. Прагнення до цієї аналогії було викликане|спричиняти| можливістю|спроможністю| використовувати апарат математичної лінгвістики, тобто методи за своєю природою є синтаксичними. Використання апарату математичної лінгвістики для опису структури зображень можна застосовувати лише|тільки| після того, як проведена сегментація зображень на складові частини, тобто вироблені слова для опису типових фрагментів і методи їх пошуку. Після|потім| попередньої роботи, що забезпечує виділення слів, виникають власне лінгвістичні задачі|задачі|, що складаються із завдань|задач| автоматичного граматичного розбору описів для розпізнавання зображень. При цьому виявляється самостійна область досліджень, яка вимагає не лише|не тільки| знання основ математичної лінгвістики, але і опанування прийомів, які розроблені спеціально для лінгвістичної обробки зображень.

Читайте також:

1. АЛЬТЕРНАТИВНІ ПІДХОДИ ДО ВИДІЛЕННЯ МЕТОДІВ УПРАВЛІННЯ
2. Визначення поняття права. Значення загального поняття права. Різні підходи до визначення поняття права.
3. Вимір дохідності та загальні підходи до оцінки ефективності управління інвестиційним портфелем.
4. Геометричний метод складання сил
5. Геометричний розподіл
6. Геометричний розподіл
7. Гіпергеометричний розподіл
8. Глобалістика: підходи до визначення, її риси та ознаки як самостійної науки.
9. Головні етапи кількісного аналізу та оцінювання ризику. Методичні підходи до визначення ризику.
10. Головні підходи до періодизації історії розвитку світової економіки та економічної думки
11. Головні підходи до праворозуміння

Переглядів: 832