• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Перетворення Лапласа

1. Оригінал

Означення 1.Комплекснозначна функція дійсної змінної називається оригіналом, якщо вона задовольняє такі умови:

1) 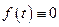при ;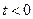

2) при 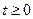функція кусково-неперервна, тобто на будь-якому проміжку має не більш ніж скінченну кількість розривів першого роду;

3) при функція має обмежений степінь зростання, тобто існує таке додатне число 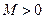і таке невід’ємне число 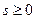, що для всіх 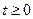виконується нерівність

.

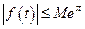Точну нижню межу (найменше значення) , для якого виконується умова 3), називають показником росту функції .

Функції-оригінали при або обмежені або прямують до нескінченності не швидше, ніж показникові функція 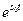. Такі функції ще називають функціями експоненціального типу.

Найпростішим прикладом оригіналу є одинична функція Хевісайда

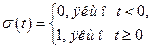
(достатньо взяти ).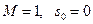

Якщо задовольняє умови 2) і 3), то функція

є оригіналом. Тому надалі для скорочення запису домовимось замість писати і пам’ятати, що при 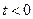рівна нулеві.

Функції є оригіналами. Проте далеко не всі функції є оригіналами. Наприклад, 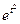не є оригіналом, бо не виконується умова 3); функція 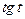теж не є оригіналом, бо не виконується умова 2).

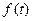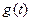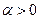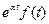Зауваження. Якщо і оригінали, то для довільних сталих функції , при , , , та 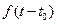також є оригіналами.

2.Зображення

Означення 2. Зображенням (перетворенням Лапласа) функції-оригіналу називається функція 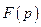комплексної змінної , що визначається інтегралом Лапласа:

.

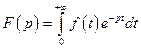Символічно перетворення Лапласа записують 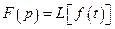або .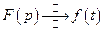

Зрозуміло, що потрібно з’ясувати, де ж інтеграл Лапласа збігається.

Теорема 1.Якщо функція – оригінал з показником росту , то інтеграл Лапласа абсолютно збігається в півплощині , а саме

,

і є в цій півплощині аналітичною функцією.

Теорема 2 (необхідна умова існування зображення).Якщо функція 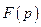– зображення функції з показником росту , то .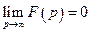

Знайдемо зображення деяких функцій, використовуючи означення.

Приклад 1.Знайти зображення одиничної функції Хевісайда.

Розв’язання. Функція є оригіналом з показником росту . Інтеграл Лапласа

.

Якщо , то 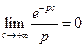. Таким чином, .

Приклад 2.Знайти зображення функції .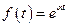

Розв’язання. Функція 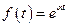є оригіналом з показником росту . Інтеграл Лапласа

.

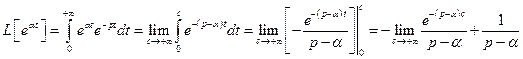Оскільки 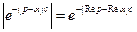, то при . Отже, .

3. Лінійність перетворення Лапласа.

Теорема 1.Нехай ,-довільні числа. Тоді

.

Доведення.

Теорема 2 (теорема єдності).Якщо , то .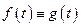

Приклад 1.Знайти зображення функції .

Розв’язання. Функція є оригіналом з показником росту . Оскільки , то за властивістю лінійності маємо при :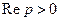

.

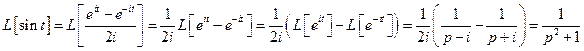Вправа.Показати, що: 1) ; 2) ; 3) .

4. Основні теореми.

Теорема 3 (теорема подібності).Якщо , де , то при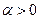

,

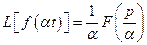де .

Доведення. За означенням перетворення Лапласа маємо

,

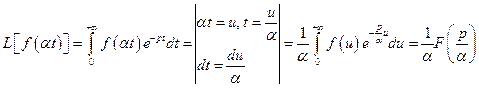оскільки .

Приклад 2. Знайти зображення функцій , , , .

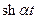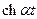Розв’язання.За теоремою подібності

; ;

; .

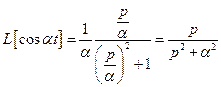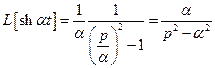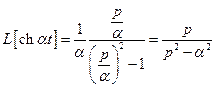Теорема 4 (теорема про зміщення зображення).Якщо , , то

,

де .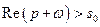

Доведення. За означенням перетворення Лапласа маємо

,

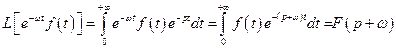де .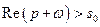

Приклад 3. Знайти зображення функцій ; .

Розв’язання.За теоремою про зміщення зображення

; .

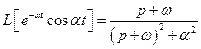Теорема 5 (теорема про запізнення). Якщо , то

,

де 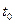– довільне додатне число.

Доведення. Функція-оригінал має вигляд:

За означенням перетворення Лапласа маємо

.

Перший інтеграл дорівнює нулю, оскільки , коли . У другому інтегралі зробимо заміну . Тоді

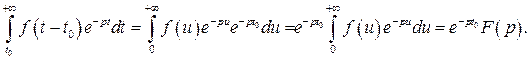
Теорема 6 (теорема про випередження). Якщо , то

,

де 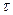– довільне додатне число.

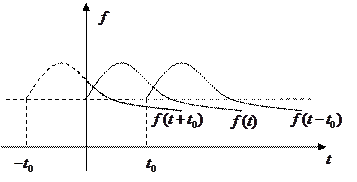Процес, що описується функцією , починається пізніше на час 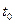ніж процес, який описується функцією , а відповідно скоріше на 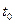, тому і відповідні теореми називаються теоремами запізнювання і випередження.

Теорема 7 (зображення періодичного оригіналу). Якщо – періодична функція, період якої , і, то .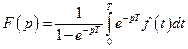

Читайте також:

1. Адаптивні хвилькові перетворення : Хвилькові пакети.
2. Визначення перетворення за Лапласом
3. Визначення. Матриці, отримані в результаті елементарного перетворення, називаються еквівалентними.
4. Визначте соціальні перетворення в процесі радянізації українського суспільства.
5. Виконаємо лінійне перетворення
6. Вимірювальні сигнали, перетворення вимірювальних сигналів, форми вимірювальної інформації
7. Вирішення проблеми не міститься в існуючому знанні та не може бути отримане шляхом перетворення наявної наукової інформації.
8. Вирішення проблеми не міститься в існуючому знанні та не може бути отримане шляхом перетворення наявної наукової інформації.
9. Властивості зворотного перетворення за Лапласом
10. Властивості прямого перетворення за Лапласом
11. Вплив легуючих елементів на перетворення в сталі
12. Встановлення комуністичного політичного режиму в Україні в 20-х – 30-х роках ХХ ст.: соціально-економічні перетворення

Переглядів: 5117