Студопедия
Новини освіти і науки:
МАРК РЕГНЕРУС ДОСЛІДЖЕННЯ: Наскільки відрізняються діти, які виросли в одностатевих союзах

РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання

ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"

ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ

Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків

Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні

Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах

Гендерна антидискримінаційна експертиза може зробити нас моральними рабами

ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ

ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів


Контакти


Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Скалярний добуток двох векторів

 

Означення. Скалярним добутком двох векторів називається число, яке дорівнює добутку їх довжин (модулів) на косинус кута між ними.


 


→

Скалярний добуток векторів aіb позначається символом

→ →

a⋅ b .За означенням

→ →   → →    
a⋅ b =   a       b   cos ϕ, (2.12)  
         

 

→

де ϕ - кут між векторами aіb (мал.21), причому 0 ≤ ϕ ≤ π

 

На основі формули (2.7) формулу (2.12) можна записати так:


 

а)

 

О


 

 

→       б)   →  
в               в  
                  φ  
φ   А              
            А →  
             
  а Мал.21. а  
       
    → →   → →    
    a⋅ b =   a   Пр→ b (2.13)  
         

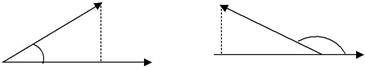a


 

або аналогічно

→ →   → →    
a⋅ b =   b   Пр→ a (2.14)  
     

b

 

Отже, скалярний добуток двох векторів дорівнює добутку мо-дуля одного з них на проекцію другого вектора на напрям першого.

 

Поняття скалярного добутку випливає із задач механіки. Відомо, що робота A сили F при прямолінійному переміщенні матеріальної точки на шляху l знаходять за формулою

∧ (2.15)  
A = F ⋅ l cos( F ,l )  

Розглянемо деякі властивості скалярного добутку:

→ → → →

1) a⋅ b = b⋅ a -переставний закон.

 

Доведення. За означенням скалярного добутку

→ →→ →   → →→ →   →→ = → →    
a⋅ b =   a       b   cos ϕ і b⋅ a =   b       a   cos ϕ , але a   b b   a як добуток  
                 
              → → = → →                                    
чисел, то a⋅ b b⋅ a .                                    
                      → → →   `→                    
  2)       λ( a⋅ b ) = ( λ a )⋅ b -сполучний закон.          
  Доведення. На   основі формули (2.14)   маємо, що  
→     →         →   →                                    
( λ a )⋅ b   =   b   Пр→ ( λ a ),                                    
                                         
                                                                   

b


 


                                  →     →  
Згідно з властивостями проекцій §6 Пр→ ( λ a ) = λПр→ a .  
                              b     b  
Таким чином,                                          
→→ →         → → →       →     →  
( λ a ) ⋅ b =   b   Пр → ( λ a ) =   b     λ Пр → a = λ     b   Пр → a .  
             
          b         b                 b    
                                →   → → →  
З другого боку, на основі формули (2.14), маємо   b   Пр→ a = a⋅ b .  
     
→   →   →   → → →   b    
             
Отже, ( λ a )⋅ b =λ(   b   Пр→ ( λ a ) =λ( a⋅ b ) .        
           

b

 

→ → → → → → →

3) a( b + c ) = a⋅ b + a⋅ c -розподільний закон.

 

Доведення. На основі формули(2.14)маємо

→→ →     →                                 → →                                            
a ( b +   c ) =   a   Пр → ( b + c ),                                            
                                                 
a →   →   →   →    
           
Згідно з властивостями проекцій Пр→ ( b + c ) =   Пр→ b +     Пр→ с      
Таким чином, a a a  
   
→ →→→                       →→→   →   →→     →→   →  
                                                                                                                     
a( b + c ) =   a     Пр→ ( b + c ) =   a   ( Пр→ b + Пр→ c ) =   a   Пр→ b +   a   Пр→ с .  
                   
a a a a a  
→ → → → → → → →  
На основі формули (2.14) маємо, що   a   Пр→ b =   а⋅ b і   a   Пр→ с = а⋅ с  
           
a a  
                        → →     →→ →   →   →→ →→ →      
Значить a( b   + c ) =       a       Пр→ b +   a   Пр→ с = a⋅ b + a ⋅ c .      
               
→ →   → 2 a a  
     
                                                                                                                           
4) a ⋅ a =   a   .    
       
Доведення. За означенням скалярного добутку                          
→ →         → →               → 2   →                                            
a⋅ a =   a       a   cos 0 =   a       , якщо a ≠ 0.                                            
                                                       
→ → → →  
Якщо a     = 0 ,то добуток a⋅ a = 0 ,але тут   a   = 0 і рівність    
           
→ → → 2  
                                                                                                             
a⋅ a =   a               також правильна.                                                                      
                                                                                     
→ →  
Скалярний добуток a⋅ a називають скалярним квадратом век-  
                                                                                               
→                       → →       → 2               → 2                 →   → 2                                        
тора a , тобто a⋅ a   = a   =   a     і звідси   a   = a .                                        
                                                   
                                                                                                                         


 


              → →   → →             → → → → = 0 .  
  5) a⋅b=0 ,якщоa ⊥ b і навпаки,якщо a ⊥ b ,то a⋅ b  
  Доведення. За   означенням             скалярного   добутку  
→ →   → →   ϕ = π , то вектори → →      
a⋅ b =   a       b   cos ϕ. Якщо a і b перпендикулярні,  
         
                                        то cos ϕ = 0 , ϕ = π ,  
                                       
                  → →     → → → →    
cos ϕ= 0 і a⋅ b = 0 .Якщо a⋅ b = 0 ,але   a       b   ≠ 0 ,  
         
                  → →                          
                                           
                                             
тобто вектори a і b перпендикулярні.                      

◙ Скалярний добуток векторів в координатній формі.

 

→ → →

 

Тому що одиничні вектори (орти) i , j , k осей Ox ,Oy,Oz

 

прямокутної системи координат взаємно перпендикулярні, то на основі п’ятої властивості скалярного добутку, маємо

  → →→ → → →→ → → →→ →    
    i ⋅ j = j⋅ i = 0 , j⋅ k = k⋅ j = 0 , i ⋅ k = k⋅ i = 0. (2.16)  
Крім цього, за четвертою властивістю скалярного добутку  
        → → → → → →      
        i ⋅ i = 1, j⋅ j = 1, k⋅ k = 1.   (2.17)  
Нехай задано два вектори з своїми координатами    
  →       →              
  a = ( x1 ; y1 ; z1 ), b = ( x2 ; y2 ; z2 ).      
Запишемо розклади цих векторів по ортам (формули 2.11)  
→   → → → → → → →    
a = x1 i + y1 j + z1 k , b = x2 i + y2 j + z2 k .    
Знайдемо скалярний добуток цих векторів    
→ →   →   → → → → →    
a b = ( x1 i + y1 j + z1 k )( x2 i + y2 j + z2 k ) .    
Використовуючи формули (2.16), (2.17) знаходимо    
          → →              
          a b = x1 x2 + y1 y2 + z1z2 (2.18)  
Таким чином, скалярний добуток двох векторів дорівнює сумі  
добутків однойменних координат цих векторів.    
        → →                
Якщо a = b , то x1 = x2 , y1 = y2 , z1 = z2 . При цьому  
отримаємо на основі рівності (2.18), що      
  → 2 = x12 + y12 + z12 , або → = x12 + y12 + z12    
  a   a (2.19)  

Довжина вектора дорівнює квадратному кореню із суми квадратів його координат.


 


Із формули (2.12) знаходимо кут між двома векторами

        → →      
      cos ϕ= a⋅ b (2.20)  
      → →    
        a   b          
Формулу (2.20) на основі формул (2.18) і (2.19) запишемо у  
вигляді cos ϕ=   x1 x2 + y1 y2 + z1z2   (2.21)  
                 
      x12 + y12 + z12 ⋅ x22 + y22 + z22  
  → →                
Якщо вектори a і b є колінеарні, то вони задовольняють  
умові (2.6) , а саме →       →      
b =λ a (2.22)  
                → →  
де скалярний множник λ > 0 , коли вектори b і a мають одинако-  

вий напрям, і λ<0 якщо протилежні напрями. Рівність (2.22) в координатній формі запишеться так:

x2 =λx1 , y2 =λy1 , z2 =λz1 або x2 = y2 = z2 = λ (2.23)  
x1 y1 z1  
               
Умова (2.23)               → →  
є умовою паралельності векторів a і b .Отже,  

→ →

 

якщо вектори a і b колінеарні, то їх однойменні координати пропорціональні і навпаки.

 

Необхідною і достатньою умовою перпендикулярності

→→ → → = 0 або в координатній формі    
векторів a і b є рівність a b    
  x1 x2 + y1 y2 + z1 z2 = 0 (2.24)  

Умова (2.24) є умовою перпендикулярності двох векторів.

→

Приклад 1.Знайти проекцію вектораa=( 4;4;2 )на напрям

 

→

вектора b = ( 2;1;2 ).

 

Розв’язування. Із формули (2.14) одержимо

 

  →   → →              
    a⋅ b   4 ⋅ 2 + 4 ⋅ 1 + 2 ⋅ 2        
  Пр→ a = =   = .  
         
  b     → 22 + 12 + 22      
      b        
              → → →     →  
  Приклад 2.Виразити через орти i , j , k   орт a вектора  
→ = ( 3;−2;6 ) .                      
a                      


 


Розв’язування. Одиничний вектор

→ →     → → →                          
a     3 i − 2 j + 6 k = → − → + →  
a =   =  
              i     j     k .  
→   32 + ( −2 )2 + 6 2  
                   
  a                  

Приклад 3.Підприємство випускає продукцію чотирьо видівв кількості 210, 160, 172 і 300 штук. Ціни в одних і тих же грошових одиницях задані в такому порядку: 4,3;1,2;7;2,1. Обчислити сумарну ціну всієї продукції.

 

Розв’язування. Запишимо дані про випуск продукції у вигляді

→

векторів а = ( 210;160;172;300 ) , а також ціни одиниці кожної із

 

→

 

виду продукції b = ( 4 ,3;1,2;7 ,0;2,1 ) .Тепер сумарна ціна П всієї продукції запишеться на основі формули 2.18.

→ →

П = a b = 210 ⋅ 4 ,3 + 160 ⋅ 1,2 + 172 ⋅ 7 ,0 + 300 ⋅ 2,1 = 2929 .

 

§12. n-мірний вектор і векторний простір

 

Множина всіх векторів, які ми розглядали на площині або в просторі і для яких визначені операції додавання векторів, множен-ня вектора на число є простими прикладами векторного простору.

 

Означення1. Упорядкована множина n дійсних чисел, за-писаних у вигляді ( a1 ,a2 ,a3 ,...,an ) називається n- мірним векто-

ром. Числа a1 ,a2 ,a3 ,...,an називаються координатами вектора
→ →  
a , тобто a = ( a1 ,a2 ,a3 ,...,an ) .

Поняття n-мірного вектора широко використовується в економіці, наприклад, деякий набір товарів можна охарактеризувати

  → = ( a1 ,a2 ,a3 ,...,an ) ,а відповідно ціни вектором  
вектором a  
→ = ( b1 ,b2 ,b3 ,...,bn ).  
b  

Якщо в n-мірного вектора одна координата дорівнює одиниці, а всі решту рівні нулю, то такий вектор називається одиничним. Очевидно, що існує n різних одиничних векторів

→   → →  
e1 = ( 1,0 ,0 ,...,0 ), e2 = ( 0 ,1,0 ,...,0 ),... en = ( 0 ,0 ,0 ,...,1 ),

які виходять із початку координат точки О. Всі означення і дії для


 


двомірних і тримірних векторів, заданих в координатній формі, роз-повсюджуються і на n-мірні вектори (n≥4).

 

Два n-мірні вектори рівні тоді і тільки тоді, коли їх відповідні компоненти рівні.

→ →    
Вектор a = ( a1,a2,a3,...,an) і вектор b = ( b1 ,b2 ,b3 ,...,bn )  
рівні, коли ai=bi(i = 1,2,3,...,n ).      
Сумоюдвохn-мірних векторів → →    
a і b є третійn-мірний вектор  

→

 

с ,координати якого дорівнюють сумі відповідних однойменних

  → →      
координат векторів a і b , тобто сi = ai + bi(i = 1,2,3,...,n ).  
    → на дійсне число λ називається вектор  
  Добуткомвектораa  
→ →        
d =λ a ,координати якого di дорівнюють добутку числа λ на  

→

відповідні координати вектора a , тобто di = λai(i = 1,2,3,...,n ).

Вектор, у якого всі координати дорівнюють нулю, називається

→

нульовим векторомі позначається0=( 0 ,0 ,...,0 ).

 

Операції над довільними векторами задовольняють влас-тивостям:

→ → → →

1. a + b = b + a -переставний закон;

  →   →→ → → →  
2. ( a + b ) + с = a + ( b + c ) −сполучний закон;  
    → → сполучний закон, відносно числового  
3. α( β a ) = ( αβ ) a -  
множника; → → → →    
    розподільчий закон відносно суми  
4. λ ( a + b ) =λ a +λ b -  

 

векторів;

→ → →

5. ( α+β ) a =α a +β a -розподільчий закон відносно суми

 

числових множників.

→ = ( 0 ,0 ,...,0 ), такий,що → → →  
6. Існує нульовий вектор 0 a + 0 = a  
→          
для довільного вектора a ;          

 


    → →
7. Для довільного вектора a існує протилежний вектор (- a ),
  → →→  
такий, що a + ( − a ) = 0.  
  → → →
8. 1 ⋅ a = a ,для довільного вектора a (особлива роль число-

вого множника 1).

Означення. Множина векторів з дійсними координатами, в якій визначено операції додавання векторів і множення вектора на число, які задовольняють вище приведеним восьми властиво-стям називається векторним простором.

→ → →

 

Зауваження. Якщо під векторамиa , bі сможна розглядати

 

елементи довільної природи, то відповідна множина елементів називається лінійним простором.

 

Лінійним простором є, наприклад, множина всіх алгебраїчних многочленів степені яких не перевищують натурального числа n . Якщо множина всіх многочленів точно дорівнює натуральному чис-лу n, то не буде лінійним простором тому, що сума двох многочленів може виявитися многочленом, степінь якого менше n.

 

Читайте також:

  1. Векторний добуток векторів
  2. Векторний добуток векторів.
  3. Векторний добуток і його властивості.
  4. Визначення модуля та напряму векторів і .
  5. Вираження мішаного добутку через координати векторів.
  6. Вуглевидобуток в Україні та перспективи його розвитку
  7. Геометричне тлумачення мішаного добутку векторів.
  8. Де - місячний видобуток руди у кар’єрі, млн.т.
  9. Декартів добуток
  10. Дисоціація води. Йонний добуток води
  11. Дисоціація води. Йонний добуток води.
  12. Добуток ланцюгових темпів зростання становить базовий темп зростання.



Переглядів: 1436

<== попередня сторінка | наступна сторінка ==>
Дії над векторами, заданими в координатній формі | Базис. Розклад вектора по даному базису

Не знайшли потрібну інформацію? Скористайтесь пошуком google:
  

© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове.


Генерація сторінки за: 0.04 сек.