Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Гіпербола та її рівняння

Означення4. Гіперболою називається множина точок площини, абсолютне значення різниці віддалей яких від двох за-даних точок, які називаються фокусами, є величина стала.

Ґрунтуючись на означенні 4 виведемо канонічне рівняння гі-перболи. Нехай задані дві точки F₁ і F₂ є фокусами гіперболи, поз-

начимо віддаль між ними через	2c ,	а абсолютну величину різниці
	y			віддалей точки гіперболи від
			точок	^F1	і F₂ позначимо
		M(х,у)
			через	2a( a > 0 ). За вісь абс-

	r₂	r₁		цис візьмемо пряму, яка про-
			ходить через фокуси, а за

F₂(-c,0)		F₁(c,0)	x	вісь ординат візьмемо пряму
перпендикулярну до вісі аб-
		Мал.58		сцис,	яка	проходить через
			середину	відрізка

F₂ F₁ (мал.58),тобто через точку 0. Тому щоF₂ F₁ = 2c ,то коорди-нати фокусів будуть відповідно F₁( c ,0 ) і F₂( −c ,0 ) , а фокальні

радіуси відповідно	r₁ = F₁ M ,		r₂ = F₂ M ,	\| r₂ − r₁ \|= 2a , де
M ( x , y ) довільна точка гіперболи.
Користуючись формулою віддалл1 між двома точками і озна-
ченням 4, маємо рівняння гіперболи
\|	( x + c )² + y² −	( x − c )² + y² \|= 2a .	(2.130)
Запишемо це рівняння в такому вигляді
	( x + c )² + y²	−	( x − c )² + y²	= ±2a	або
	( x + с )² + y²	=	( y − c )² + y²	± 2a .	(2.131)

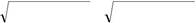
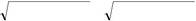
Підносячи до квадрату обидві частини цього рівняння, одер-жимо,

x² + 2cx + c² + y² = x² − 2cx + c² + y² ± 4a	( x − c )² + y² + 4a² ,
або після спрощення xc − a² = ±a ( x − c )² + y²	. Знову підносячи

обидві частини одержаного рівняння до квадрату, одержимо після спрощень

x² ( c² − a² ) − a² y² = a² ( c² − a² ) .

(2.132)

Розділивши обидві частини рівняння (2.132) на a²( c² − a²),

одержимо

x²

−

y²

= 1 .

(2.133)

c² − a²

a²

Покажемо, що c² − a² > 0

( c > a ). Тому що в будь-якому

трикутнику різниця

двох

сторін

менша

третьої, то

| F₂ M − F₁ M |< F₂ F₁ , або

2a < 2c , або a < c .Тоді

c² − a² величина

додатна і її позначимо черезb² . Тобто

c² − a² = b² .

(2.134)

Підставляючи (2.134) в (2.133), одержимо канонічне рівняння

гіперболи

x²

−

y²

= 1 .

(2.135)

a²

b²

Рівняння (2.135) є рівняння другого степеня, значить гіпербо-ла є крива другого порядку. Дослідимо форму гіперболи за її рів-нянням (2.135). Оскільки рівняння містить x і y тільки в парних

степенях, то гіпербола симетрична відносно обох осей координат. Знайшовши y та x із рівняння (2.135), одержимо

y = ±		b		x²	− a² ,	(2.136)
	a

x = ±	a		y²	+ b² .	(2.137)
b

Із рівняння (2.136) можна зробити такі висновки:

а) значення у уявні, якщо |х|<a значить гіпербола не перетинає вісі Оу і не має точок, що знаходяться в полосі, обмеженій прямими

х=± a.

б) коли x = ±a , y = 0 , значить гіпербола перетинає вісь абс-

цис у двох точках A₁( a ,0 ) і A₂( −a ,0 ) , які називаються вершинами

гіперболи.

в) для кожного | x |> a , ордината y має два значення, які від-

різняються тільки знаком, звідси випливає, що гіпербола симетрич-на відносно осі 0 x.

Рівняння (2.137) показує, що гіпербола симетрична і відносно

вісі 0 y.

При необмеженому зростанні абсциси x ордината також нео-

бмежено зростає. Так

як гіпербола знахо-

диться поза полосою, М(х,у)

обмеженою прямими

В₁(0,в)

x = ±a , то гіпербола F₂(-c,0) F₁(c,0)

складається Із двох

окремих віток (мал.59). А₂(-а,0) _О А₁(а,0)

Відрізок A₂ A₁

В₂(0,-в)

називається дійсною

віссю гіперболи, а точ-

мал.59

ки A₁ ( a ,0 ) і A₂ ( −a ,0 ) вершинами гіперболи.Відрізок B₁ B₂ ,що

з’єднує точки В₁( 0 ,b ) і В₂ ( 0 ,−b ) називається уявною віссю гіпер-

боли. Точки F₁( c ,0 ) і F₂( −c ,0 ) називаються фокусами гіперболи.

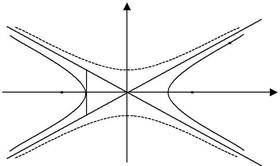
Гіпербола, яка визначається рівнянням − x² + y² = 1 має дій-

a² b²

сну вісь B₂B₁ = 2b, а уявну вісь A₂A₁ = 2a (показано на мал.59 пу-нктиром) називається спряженою по відношенню до гіперболи

x² ₋ y² ₌ ₁ _. a² b²

Якщо дійсна і уявна осі рівні, то гіпербола називається рі-вносторонньою, а її рівняння буде x²−y²=a² .

Степінь стискування гіперболи характеризується її ексцентри-ситетом.

Означення5. Ексцентриситетом гіперболи називається відношення віддалі між фокусами 2с до довжини її дійсної вісі 2a , тобто

ε = 2c = c . (2.138)

2a a

Так як для гіперболи с > a , то ε > 1.

Примітка. Для гіперболи легко показати як пов’язані r₁ і r₂ з

ε , а саме r₁ =−a +εx ( x > 0 ) ,

^r2 = a +εx ( x > 0 ) ; (2.139)

r₁ = a − εx ( x < 0 ),

r₂ =−a − εx ( x < 0 ) . (2.140)

Формули (2.139) і (2.140) одержуються аналогічно як і для еліпса.

Представляємо читачеві самостійно переконатися в справед-

ливості формул (2.139) і (2.140).

Читайте також:
V Процес інтеріоризації забезпечують механізми ідентифікації, відчуження та порівняння.
Асимптотичний підхід до порівняння оцінок
Бюджетний контроль - це порівняння показників бюджету зі звітом за відповідний період часу.
В обох випадках основним розрахунковим рівнянням є рівняння теплопередачі і теплового балансу
Вивід основного рівняння фільтрації
Використання рівняння номінальних витрат за моделлю COCOMO II
ВПРАВА 2. Утворіть де можливо, форми ступенів порівняння від поданих прикметників.
Гармонічні коливання. Диференціальне рівняння гармонічних коливань та його розв’язок. Амплітуда, фаза, частота, період коливань
Гіпербола
Гіпербола
Гіпербола
Гіпербола та її застосування

Переглядів: 1772

<== попередня сторінка | наступна сторінка ==>

Еліпс і його рівняння | Асимптоти гіперболи

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.008 сек.