
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Послідовність, яка має скінчену границю, називається збіжною, у протилежному випадку - розбіжною.
Основні теореми про границі числових послідовностей ТЕОРЕМА 1. Послідовність може мати тільки одну грани-
Цю.
Доведення. Припустимо,щоlim xn=aіlim xn=b,при чому
n→ ∞ n→ ∞
a≠b.
Виберемо ε = 1a − b . Згідно з означенням границі послідов-


 3
3
ності виконуються нерівності
| xn | − a | < | a − b | для n > N | 1 , | ||||||

xn − b < 1 a − b для n > N2 .




 3
3
Візьмемо тепер натуральне число N , більше за N1 і N2 . Отже, для n>N одночасно будуть виконуватися обидві вище
написані нерівності, на основі яких одержуємо
a − b = ( a − xn ) + ( xn − b ) ≤ a − xn + xn − b = xn − a +









 + xn − b < 2 a − b .
+ xn − b < 2 a − b .




 3
3
Звідси знаходимо, що a − b < 2a − b , а це неможливо, якщо




 3
3
a ≠ b. Таким чином,наше припущення,що послідовність може ма-ти різні границі, привело до протиріччя. Збіжна послідовність може мати тільки одну границю. Теорема 1 доведена.
ТЕОРЕМА 2. Нехай послідовності (xn) і (yn) мають відпо– відно границі aіb Тоді сума (xn+yn) (різниця (xn-- yn)) має грани-цю, яка дорівнює a+b ( a−b ) , тобто
| lim ( xn | ± yn | ) = lim xn | ± lim yn = a ± b . | (3.7) |
| n→ ∞ | n→ ∞ | n→ ∞ |
ТЕОРЕМА 3. Нехай послідовності ( xn ) і ( yn ) мають від-повідно границі aіb. Тоді і їх добуток ( xn⋅yn ) має границю, яка дорівнює a⋅b , тобто
| lim( xn ⋅ yn | ) = lim xn | ⋅ lim yn = a ⋅ b. | (3.8) |
| n→∞ | n→∞ | n→∞ |
З теореми 3 випливають такі наслідки .
1. Сталий множник можна винести за знак границі.
Справді, нехай xn = C , а yn має границю. Тоді
| lim ( xn ⋅ yn ) = lim xn | ⋅ lim yn = C lim yn . | (3.9) | |||
| n→ ∞ | n→ ∞ | n→ ∞ | n→ ∞ | ||
| 2. Якщоlim xn = a і k - натуральне число, то | |||||
| n→ ∞ | |||||
| lim xnk = (lim xn )k | = ak . | ||||
| n→∞ | n→∞ | ||||
| ТЕОРЕМА 4. Нехай послідовності ( xn ) і ( yn ) мають скі- | |||||
| нчені границі, які відповідно дорівнюють | lim xn = a , | lim yn = b | |||
| n→ ∞ | n→ ∞ |
причому b≠0. Тоді і їх відношення
( xn ) має скінчену границю,яка дорівнює a ,тобто
  yn yn
| b | ||||||||||
| xn | lim x | n | a | ||||||||
| lim | = | n→ ∞ | = | . | (3.10) | ||||||
| n→ ∞ yn | lim yn | b | |||||||||
| n→ ∞ | |||||||||||
| ТЕОРЕМА 5. Послідовність ( xn ) , яка має границю, є об- | |||||||||||
| межена. | |||||||||||
| ТЕОРЕМА 6. Нехай члени послідовностей ( xn ), ( yn ) , ( zn ) | |||||||||||
| при всіх | значеннях n=1,2,... задовольняють | нерівності | |||||||||
| xn ≤ yn ≤ zn | і lim xn | = lim zn = a .Тоді | lim yn = a . | ||||||||
| n→ ∞ | n→∞ | n→ ∞ |
Доведення.Оскільки числоaє границею послідовності( xn),то згідно означення границі послідовності для будь-якого ε > 0 іс-
| нує таке число, наприклад N1 , | що для всіх | n ≥ N1 виконується | ||||
| xn − a | < ε або a − ε < xn < a + ε , | n ≥ N1 . | N 2 ,що при n ≥ N2 | |||
| Аналогічно існує таке число, наприклад, | ||||||
| a − ε< zn < a +ε ,n≥ N2 . | ||||||
| Тоді, взявши число N більше за N1 і N2 | і використавши умо- |
ву теореми 6 та попередні нерівності, дістанемо a − ε < yn < a + ε при n≥N, що рівносильно yn − a < ε при n≥N.


Остання нерівність й доводить теорему 6.
Означення. Нехай (xn) задана послідовність і (nk) - довільна зростаюча послідовність натуральних чисел, то послідовність ( xnk ) називається підпослідовністю послідовності (xn).
З означення границі послідовності випливає правильність тве-рдження.
ТЕОРЕМА 7. Якщо послідовність ( xn ) має границю a , то й будь-яка її послідовність має ту саму границю a .
Справді, якщо число a є границею послідовності ( xn) , то для будь-якого числа ε > 0 в ε - окіл ( a − ε ,a + ε ) точки a потрап-ляють всі члени цієї послідовності, починаючи з деякого номера N . Проте, тоді в цей окіл потрапляють і всі члени послідовності ( xnk)
як тільки nk > N . А це означає, що число a є границею
| послідовності ( xn | ) , тобто lim xn | = a . | |
| k | k →∞ | k |
Примітка 1. Враховуючи(3.8)і(3.9),маємо таке твердження:сталий множник виноситься за знак границі, тобто
| lim Cxn = C lim xn . | (3.11) | ||||||
| n→ ∞ | n→ ∞ | ||||||
| Примітка 2 У вищій математиці,якщо у граничному переході | |||||||
| вигляду (3.10) одержується дія | a | , то кажуть, що дія допустима і в | |||||
| ∞ | |||||||
| результаті одержуємо нуль. Наприклад, lim | = ( | ) = 0. | |||||
| n→ ∞ n | ∞ | ||||||
З другої сторони будемо вважати , якщо у граничному
переході вигляду (3.10) одержується дія (a) , a ≠ 0 , то
 0
0
результатом такого граничного переходу є відповідь нескінченість. Наприклад,
| lim n2 = lim | = | = ( | ) =∞ . | |||||||||||
| n→ ∞ | n→ ∞ | lim | ||||||||||||
| n2 | ||||||||||||||
| n→ ∞ n2 | ||||||||||||||
| Примітка 3. Якщо при граничних переходах(3.8)-(3.10)оде- | ||||||||||||||
| ржуються вирази такого вигляду: ∞ − ∞ ; | ; | ∞ | ; 0 ⋅ ∞ , то такі вирази | |||||||||||
| ∞ | ||||||||||||||
будемо називати невизначеними.
3.4. Деякі правила розкриття невизначеностей (∞∞)
Наприклад, нехай потрібно знайти границі :
| 1) lim | n2 | − 3 | ; | 2) lim | n5 + n4 + n | ; | 3) lim | n7 + n + 1 | . | |
| n→ ∞ n3 + n | n→ ∞n2 + n | n→ ∞ n7 + n2 |
Розділивши чисельник і знаменник на найвищий степінь n у даних прикладах, одержуємо:
| n2 − 3 | − | n5 + n4 + n | ||||||||||
| ; 2) | = | |||||||||||
| 1) | = | n | n3 | |||||||||
| n3 + n | + | n2 + n | ||||||||||
| n2 | ||||||||||||
| 1 + | + | |||||||||
| n4 | ||||||||||
| n | ; | |||||||||
| + | ||||||||||
| n | n | |||||||||
| 3) n7 + n+1 = 1+ n6 | + n7 . | ||||||||||||
| n7 + n2 | |||||||||||||
| 1+ | n5 | ||||||||||||
| Далі, використовуючи основні теореми про границі, і здійс- | |||||||||||||
| нюючи граничний перехід приn → ∞ , одержуємо такі | |||||||||||||
| відповіді: 1) | lim n2 − 3 = lim n − n3 = 0 − 0 ;= 0 = 0; | ||||||||||||
| n→ ∞ n3 + n | n→ ∞ | 1 + | 1 + 0 | ||||||||||
| n2 | |||||||||||||
| 2) | lim n5 + n4 + n = lim | 1 + n | + n4 | =∞ ; | |||||||||
| n→ ∞ | n2 + n | n→ ∞ | |||||||||||
| n3 + n4 | |||||||||||||
| 3) | lim n7 + n + 1 = lim | 1 + n6 | + n7 | = 1 + 0 + 0 = 1. | |||||||||
| n→ ∞ n7 + n2 | n→ ∞ | + | 1 + 0 | ||||||||||
| n5 | |||||||||||||
| 3.5. Павутинна модель ринку | |||||||||||||
| Розглянемо найпростішу модель ринку одного товару і | |||||||||||||
| процес пошуку (“нащупування”) рівноважної ціни. Це є одна з | |||||||||||||
| основних проблем ринку, яка означає фактично торг між виро- | |||||||||||||
| бником (продавцем) і покупцем. | |||||||||||||
| Ми уже розглядали функції попиту і пропозиції від ціни на | |||||||||||||
| товар, а також їх графіки. Зрозуміло, що в загальному випадку ці | |||||||||||||
| залежності | нелінійні. | Для | Р | ||||||||||
| спрощення | ситуації, | графіки | P1 | S1 | |||||||||
| цих функцій можна | замінити | ||||||||||||
| P3 | |||||||||||||
| прямими | (графіками | дотичних | |||||||||||
| до цих кривих в заданих точ- | P4 | ||||||||||||
| P0 | |||||||||||||
| ках). Нехай спочатку виробник | P5 | ||||||||||||
| (продавець) визначає ціну P1 | на | P2 | S | Q | |||||||||
| товар. Зрозуміло, що ця ціна P1 | |||||||||||||
| Q2 | Q3 Q1 S,Q | ||||||||||||
| є вищою за рівноважну (кож- | |||||||||||||
| S0 | |||||||||||||
| ний виробник хоче мати найбі- |
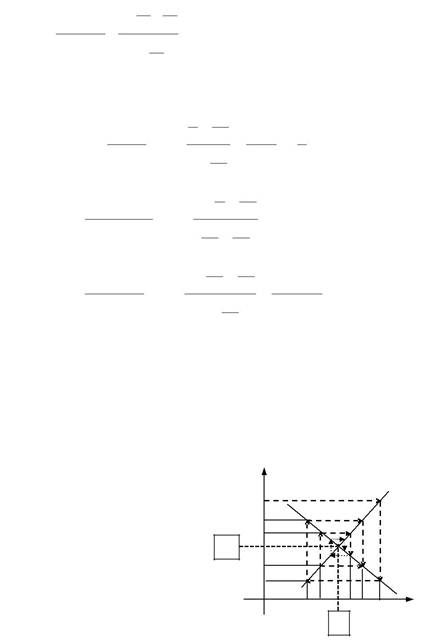
льший прибуток від виробництва товарів). Покупець оцінює попит Q1 при цій ціні і визначає свою ціну P2 ,при якій цей попит Q1 рів-
ний пропозиції S1 . Ціна P2 нижча рівноважної (кожний покупець
хоче купити дешевше товар). В свою чергу продавець оцінює попит Q2 ,що відповідає ціні P2 ,і визначає свою ціну P3 і т.д.Процес
торгу продовжується і в кінцевому випадку приведе до рівноважної ціни P0 ( павутина закручується). Якщо розглянути послідовність
| чисел p1, p2, p3,..., то ця послідовність має границю P0 | = lim Pn . | ||||||
| n→ ∞ | |||||||
| Ми розглянули збіжну модель. Зрозуміло, що може бути і ро- | |||||||
| збіжна модель, тобто рівноважну ціну | Р | ||||||
| знайти не можливо. | P1 | ||||||
| Розглянемо малюнок. | S1 | ||||||
| В даній ситуації, нехай вироб- | |||||||
| P0 | |||||||
| ник (продавець) визначає ціну Р1 на | |||||||
| P2S2 | |||||||
| товар. Очевидно, що ця ціна є вищою | |||||||
| за рівноважну. Покупець оцінює по- | Q | ||||||
| пит | Q1 при цій ціні і визначає свою | Q2S,Q | |||||
| Q1 | S0 | ||||||
| ціну | Р2 ,при якій цей попит Q1 рів- | ||||||
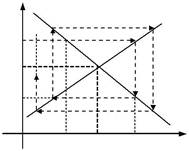
ний пропозиції S1 . Ціна Р2 нижче рівноважної і т.д.
Процес торгу продовжується і павутина розкручується. Якщо розглянути послідовність чисел p1, p2, p3,..., то ця послідовність
розбігається: lim pn = ∞ .
n→ ∞
3.6. Існування границі монотонної числової послідовності ТЕОРЕМА. Якщо послідовність x1 , x2 ,..., xn ,... є монотонно
Читайте також:
- D називається обмеженою зверху (знизу), якщо існує число М
- А середній коефіцієнт росту в такому випадку визначається як
- Акта спеціального розслідування нещасного випадку.
- Але відмінні від значення функції в точці або значення не існує, то точка називається точкою усувного розриву функції .
- Безрозмірною характеристикою гідротрансформатора називається залежність коефіцієнтів пропорційності моментів насосного і турбінного коліс від його передаточного відношення.
- В крайньому випадку, записи мають бути тезисні, в які ви можете заглянути у крайньому випадку (при загрозі краху, загибелі тощо).
- Взаємодія йонів солі, що утворюються в результаті електролітичної дисоціації з молекулами води, називається гідролізом солі.
- Визначення. Точка О називається полюсом, а промінь l – полярною віссю.
- Визначення: Площина, що проходить через дотичну й головну нормаль до кривої в точці А називається дотичною площиною.
- Виникнення однорідних травм у людей, що перебувають у подібних умовах праці і побуту, називається травматизмом.
- Випадку смерті на підприємстві, а також зникнення працівника під час
- Вогнегасником називається переносне чи пересувне обладнання для гасіння осередків пожежі за рахунок випуску запасеної вогнегасної речовини.
| <== попередня сторінка | | | наступна сторінка ==> |
| З якого виконується нерівність | | | Зростаючою (спадною) і обмежена зверху (знизу), то вона збіжна. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |