Студопедия
Новини освіти і науки:
МАРК РЕГНЕРУС ДОСЛІДЖЕННЯ: Наскільки відрізняються діти, які виросли в одностатевих союзах

РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання

ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"

ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ

Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків

Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні

Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах

Гендерна антидискримінаційна експертиза може зробити нас моральними рабами

ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ

ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів


Контакти


Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Перша визначна границя

Для розкриття невизначеностей вигляду (0) у тригонометри-

                                                 
чних виразах користуються таким твердженням.      
  ТЕОРЕМА 2. Функція f ( x )= sin x   при x→0 має грани-  
    x  
                                               
цю, що дорівнює 1, тобто lim= sin x = 1 - перша визначна гра-  
       
ниця.                     x →0   x        
                                           
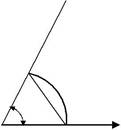
  Доведення. Якщо x є кут,виміряний у радіанах, 0 < x <π,то  
                                               
(див. мал.) для площ трикутника OAB ,сектора OAmB трикутника  
OCB правильні нерівності ( OA = OB = R ) .     С  
     
    S OAB < Sсект.OAmB < S OCB або        
    R2 sin x < R2 x <   R2 tgx .        
                 
                        А m    
  Після скорочення на число   R2 діста-    
         
       
немо sin x < x < tgx .                   О х   х  
                         
                         
  Поділивши почленно на sin x , знайдемо В  
       
1 < x < , звідси 1 > sin x > cos x.        
sin x              
    cos x       x                    
  Помноживши останню нерівність на (-1) і додавши (+1 ) до  
кожної частини знайдених нерівностей, маємо      
  0 < 1 − sin x < 1 − cos x.                    
                       
            x                              
  Використовуючи нерівність sin x < x ( 0 < x <π ) і      
                                                 

перетворюючи вираз 1 − cos x , знаходимо

 


1 − cos x = 2 sin2 x < 2 x   x = x2 .  
           
                2 2        
Тому 0 < 1 − sin x < x2 .   (A)  
           
    x                      
Покажемо правильність нерівностей (A) і для − π < x < 0 .  
                                       
Візьмемо допоміжну змінну y =− x. Оскільки 0 < y <π,то за  
                                       
доведеним вище 0 < 1 − sin y < y2 .  
       
                  y        
Підставивши замість y число (-x),дістанемо  
0 < 1 − sin( − x ) < ( − x )2      
         
  − x                          

і, зважаючи на непарність функції sinx, знайдемо

 

0 < 1 − sin x < 1 x2 ,тобто нерівність(А)правильна для всіх x 2

( −π , π ), x ≠ 0 .

2 2

Для наперед заданого числа ε > 0 число δ > 0 візьмемо таким,

що дорівнює 2ε.Тоді з нерівностей

0 < x − 0 = x <δ= 2εвипливатиме нерівність

sin x − 1 = 1 − sin x < x2 < ( 2ε )2 =ε.  
x x      
       

А це означає, згідно означення 3, що границя функції sin x в x

точці x=0 дорівнює одиниці. Теорему доведено .

 

  Приклад 1.lim sin ax = lim sin y = a lim sin y   = a.  
               
    x →0   x       y →0   y       y →0 y              
  Приклад 2.                 a                            
                                             
  1 − cos 5 x   2 sin   x       sin x          
                       
lim = lim             = 2 lim         = 2 ⋅ ⋅ = .  
x2   x2           x          
x →0 x →0       x →0      

 


4.4. Допоміжні твердження = 1 ,де xi > 0 , i = 1,2,...,n,  
ТЕОРЕМА 3. Якщо x1⋅x2⋅...⋅xn  
то∑n xi ≥ n ,причому рівність має місце тільки тоді, коли  
i = 1      

x1 = x2 = ... = xn = 1 .

 

ТЕОРЕМА 4. Середнє геометричне n додатніх чисел xi , i = 1,2,...,n, менше або дорівнює їх середньому арифметичному,

тобто n x1⋅x2 ...xn ≤   x1 + x2 + ... + xn , причому рівність справ-  
       
                            n    
джується тільки тоді, коли x1=x2=...=xn .    
Доведення. Позначивши через q = n x1 ⋅ x2 ..⋅ xn затеоремою3  
з рівності x1 ⋅ x2 ... xn = 1 випливає нерівність    
             
      q   q q    
  x1 + x2 ...+ xn ≥ n або q ≤ x1 + x2 + ...+ xn , причому рів-  
    q q      
  q                   n    
                                     

ність має місце тільки тоді, коли x1 = x2 = ... = xn. Теорема доведе-на.

 

4.5. Число e. Друга визначна границя

Для розкриття невизначеності (1 ∞ ) використовують таке тве-

 

рдження:        
ТЕОРЕМА 5. Послідовність yn = ( 1 + )n , n ∈ N має  
   
границю.   n  
       

Доведення. Використовуючи твердження теореми4,маємо

 

                    1 + ( 1 + ) ⋅ n        
                           
n+ 1 1 ⋅ ( 1 + n <           n     = 1 +    
  )                         .  
n     n + 1        
                          n + 1  
Звідси                                          
  n               n+ 1                    
( 1 +   )   < ( 1 +   )     ,                
n   n + 1                  
тобто послідовність   yn = ( 1 + ) n , n ∈ N ,монотонно зростає.  
         
                          n            


 


Аналогічно для послідовності zn = ( 1 −   n   ∈ N ,маємо  
  ) , n  
n  
                                             
              1 + ( 1 − ) ⋅ n                
                       
n+ 1 1 ⋅ ( 1 −   ) n <         n   = 1 −   .      
n       n + 1                
                      n + 1      
Звідси ( 1 −     n < ( 1 −     n+ 1                
    )     )   .              
  n   n + 1                


Таким чином, послідовність   = ( 1 − n   ∈  
zn   ) , n  
n  
монотонно зростає.            
             
Оскільки              

 

N ,також


( 1 + )n+ 1 = ( n + 1 )n+ 1 = ( n )− ( n+ 1 ) = ( 1 − )− n+ 1 =

 


,


n n         n + 1 n + 1  
то послідовність xn = ( 1 + n+ 1 , n ∈ N , спадає.  
      )  
  n  
                   
Тому yn = ( 1 +   n < ( 1 +   n+ 1 ≤ x1 = 4 , n ∈ N .  
  )         )  
    n  
  n            

 

zn+ 1


Тобто (yn)- обмежена послідовність і вище було показано , що вона зростає.

Отже, послідовність yn = ( 1 + )n має границю.Цю границю  
   
    n      
в математиці позначають буквою e , тобто lim ( 1 + )n = e .  
   
      n→ ∞ n  

Таку границю називають другою визначеною границею для послідовностей. Доведено, що число e – ірраціональне число і його розклад в десятковий дріб з деякою точністю має вигляд

e =2,718281828459045…

Логарифм числа x>0 за основою e називається натуральним логарифмом і позначається символом ln x. Оскільки за означенням

 

логарифма правильна рівність x = eln x , то прологарифмувавши її за основою 10, маємо lg x = М ⋅ ln x , де M = lg e = 0 ,434294.... Число

 

M називають модулем переходу від натурального логарифма до ло-гарифма десяткового.

 

Далі доведемо існування границі функції f ( x ) = ( 1 + x )x в


 


точці x = 0 . Цю границю називають другою визначною границею для власної функції.

                                                                                       
ТЕОРЕМА 6. Правильна рівність lim( 1+x )     = e.    
x    
                                                        x →0                                  
                                                                                             
                                                                   
Доведення. Спочатку доведемо рівність     lim ( 1 + x ) x = e.  
                                                                x→0 + 0                  
Можемо вважати 0 < x ≤ 1 . Для кожного x ∈ (0 ,1] існує нату-  
ральне число n = n( x ) таке, що     < x ≤ .                                
n + 1                                
                                                      n                                  
Звідси 1 +         < 1 + x ≤ 1 + .                                                  
n +                                                      
                                  n                                                  
Оскільки n + 1 >   ≥ n ,то                                                        
                                                         
                          x                                                                  
                                                         
    n                             x                       n+ 1  
              x                           x  
( 1 +   n + 1 )   ≤ ( 1 + n + 1 )     < ( 1 + x )       ≤ ( 1 + n )     < ( 1 + n )    
    n+ 1                                                                        
                                                                                     
  ( 1 + n + 1 )                           1 n                                        
або     < ( 1 + x ) x < ( 1 +   ⋅ ( 1 +                            
                        )       ).                      
                    n                      
1 +                                         n                                        
n + 1                                                                                  
                                                                                         
Якщо x → 0 + 0 , то n → ∞ . Крайні частини останніх нерівно-  
стей мають границі при n → ∞ , що дорівнюють числу e .    
                                                                                               
Звідси за теоремою 6 §3 і функція ( 1 + x )     при x → 0 + 0    
x    

 

матиме праву границю, що дорівнює e .

 

 

Покажемо, що і ліва границя функції ( 1 + x )x в точці x = 0 дорівнює числу e . Введемо нову змінну y , зв’язану із змінною x

рівністю y = −   x .                                
                                 
+ x                              
Зазначивши, що x = −     y   , дістанемо        
               
                    1 + y              
            y − 1+ y       − 1−    
                           
( 1 + x ) x = ( 1 −     )     y = (     ) y = ( 1 + y ) y ⋅ ( 1 + y ).  
            + y  
        + y                  

 


Якщо x прямує до нуля зліва, то y = −   x прямує до нуля  
     
+ x  

справа. Звідси, враховуючи, що згідно доведеного вище твердження

 

           
                 
lim ( 1 + y ) y   = e , маємо  
у→0 + 0                
       
lim ( 1 + x )     = lim (( 1 + y ) y ( 1 + y )) = e ⋅ 1 = e.  
x    
x →0 −

Читайте також:

  1. В Харкові відбулася перша персональна виставка творів художника, на якій було виставлено 120 творів.
  2. Взаємне положення площин. Перша позиційна задача
  3. Види кровотеч і перша допомога
  4. Види ушкодження опорно-рухової системи і перша допомога при них
  5. Визначений інтеграл, як границя інтегральних сум
  6. ГРАНИЦЯ САМОЗАЙМАННЯ
  7. Границя функції
  8. Границя функції двох змінних
  9. Границя функції на нескінченності
  10. Границя функції. Означення границі функції за Гейне й за Коші.
  11. Границя числової послідовності
  12. Еластичністю попиту відносно ціни називається границя відношення відносного приросту попиту до відносного приросту ціни при умові, що приріст ціни прямує до нуля.



Переглядів: 860

<== попередня сторінка | наступна сторінка ==>
Означення границі функції | Порівняння нескінчено малих величин

Не знайшли потрібну інформацію? Скористайтесь пошуком google:
  

© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове.


Генерація сторінки за: 0.029 сек.