• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Система векторів і спосіб її задання. Лінійна комбінація векторів

Лінійний простір

Векторний простір називається лінійним, якщо у ньому визначено операції над векторами – додавання і множення на число. Проте лінійний простір може бути утворений об’єктами будь-якої природи. Нехай Е - дана множина і x ,y, z … -її елементи; К – множина усіх дійсних (або усіх комплексних) чисел α, β, γ … .Нехай кожній парі x,y елементів множини Е поставлено у відповідність деякий елемент тієї самої множини,який позначається х + у і називається їх сумою. Нехай кожному елементу Х множини Е і кожному числу А із К поставлено у відповідність деякий елемент множини Е, який позначається α х і називається добутком числа α на елемент х. Множина Е називається дійсним(відповіднокомплексним) лінійним векторним простором,а її елементи, незалежно від їхньої природи, називають векторами. Так,множина многочленів не вище даного степеня зі звичайними операціями додавання і множення на числа є лінійними векторним простором .У цьому розумінні кожний такий многочлен можна назвати вектором. Множина функцій,неперервних на даному інтервалі, також називається векторним простором , і у цьому розумінні кожна така функція може бути названа вектором.

Нехай задано систему векторів a₁ , a₂ ,…, a_k в n-вимірному просторі:

Складемо із компонент векторів прямокутну таблицю, яка називається прямокутною матрицею і позначається буквою А:

або

Таким чином, задання системи векторів у n-вимірному просторі означає задання матриці, яку складено з компонент векторів даної системи. Для одновимірного простору, n= 1, матриця перетворюється або на матрицю-рядок, або на матрицю-стовпець.

Для двовимірного простору (n=2) матриця набуває вигляду

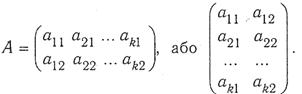
Для тривимірного простору (n=3) маємо

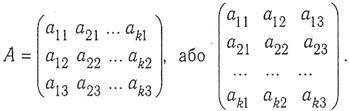
Нехай дано k векторів Помножимо кожний вектор на число λ_j , де j =1,2,…,k, і знайдені результати додамо. У результаті цього дістанемо вектор, який називається лінійною комбінацією даних векторів:

Числа λ_j називаються коефіцієнтами даної лінійної комбінації.

Якщо вектор має компоненти (a_1j, a_2j, … , a_nj), а вектор має компоненти (b₁ , b₂ ,…, b_n), то рівність запишеться у вигляді

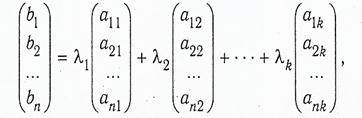(2.2)

або

Ці рівності рівносильні. У першому випадку залежність записано у векторній формі, а у другому – в скалярній.

Розглянемо питання про те, чи може дорівнювати нулю лінійна комбінація векторів:

Якщо рівність можлива за умови, що принаймні одне з чисел λ_j де j=1, 2,…,k, не дорівнює нулю, то система даних векторів називається лінійно залежною, а рівність називається нетривіальною. Якщо ж рівність можлива лише за умови, що всі λ_j=0 одночасно дорівнюють нулю, то система даних векторів називається лінійно незалежною,а рівність - тривіальною.

Читайте також:

1. Active-HDL як сучасна система автоматизованого проектування ВІС.
2. I спосіб.
3. II. Бреттон-Вудська система (створена в 1944 р.)
4. IV. Система зв’язків всередині центральної нервової системи
5. IV. УЗАГАЛЬНЕННЯ І СИСТЕМАТИЗАЦІЯ ВИВЧЕНОГО
6. V. Систематизація і узагальнення нових знань, умінь і навичок
7. VI. Система навчаючих завдань для перевірки кінцевого рівня завдань.
8. VI. Система навчаючих завдань для перевірки кінцевого рівня завдань.
9. VI. Узагальнення та систематизація знань
10. VII. Закріплення нового матеріалу і систематизація знань.
11. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
12. Автоматизована система ведення державного земельного кадастру

Переглядів: 2079