Робоча формула

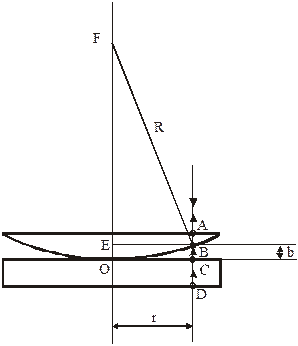Кільця Ньютона спостерігаються тоді, коли сферична поверхня опуклої лінзи великого радіуса кривизни стикається з плоскою поверхнею. Внаслідок цього між лінзою і пластинкою утворюється повітряний шар змінної товщини (рис.). Проведемо розрахунки кілець Ньютона, що спостерігаються у відбитому світлі. У цьому випадку інтерферуватимуть промені, відбиті від верхньої і нижньої меж повітряного шару (точки С і В відповідно). Отже, лінії максимумів та мінімумів проходять через точки, що відповідають однаковій товщині повітряного шару і тому називаються смугами однакової товщини. Якщо промені падають нормально на плоску поверхню лінзи, то внаслідок малої кривизни лінзи можна вважати, що відбиваються вони теж вздовж нормалі. Для різниці ходу променів дістанемо

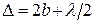. (65.4)

Рисунок 3.3

де b – товщина шару повітря між лінзою і пластиною. Доданок

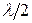відображає зміну фази хвилі, відбитої від оптично більш густого середовища (точка С). У відповідності з (65.4) різниця ходу хвиль в даному експерименті визначається тільки товщиною повітряного шару, тому вона є однаковою для всіх хвиль, відбитих на однаковій відстані від геометричного центра системи (точка О). Внаслідок цього інтерференційна картина має вигляд концентричних кілець. В центрі картини, де

, спостерігають темний круг, що відповідає різниці ходу відбитих хвиль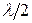

. Результат інтерференції залежить від оптичної різниці ходу хвиль. Зв’язок між радіусом інтерференційного кільця r, радіусом кривизни лінзи R і довжиною хвилі

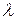можна знайти з використанням цілком простих геометричних міркувань. З ΔBEF (рис.) маємо:

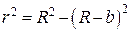. Оскільки лінза має великий радіус кривизни, то можна записати –

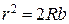, звідки

, а тому

. Радіуси світлих кілець знайдемо з умови максимуму –

, (65.5)

а радіуси темних кілець

. (65.6)

Звідси

. (65.7)

У виразах (65.4) і (65.6) 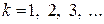– порядковий номер кілець.

Оскільки практично не вдається досягти щільного прилягання пластини до лінзи, то більш точний результат буде, коли визначається R за різницею радіусів двох довільних кілець 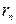і 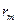. Тоді формула (65.7) набере вигляду:

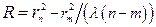. (65.8)

Підрахунок темних кілець починається від k=0, тобто від самого центра інтерференційної картини. Підрахунок світлих кілець починається з одиниці (k=1).

Для великих порядків інтерференції може відбуватися перекриття спектрів, що приводить до розмивання інтерференційної картини. Очевидно, що умовою зникнення інтерференційної картини є

, (65.9)

звідки , тобто чим більша монохроматичність світла, тим більшу кількість максимумів можна спостерігати. Крім того, остання залежність дає змогу визначити смугу пропускання фільтра за допомогою вимірювання кількості видимих інтерференційних кілець:

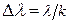. (65.10)

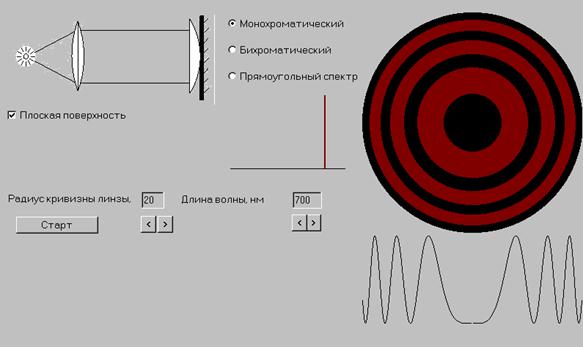
Інтерфейс програми “Кільця Ньютона”

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Теоретичні відомості	\|	Завдання 1. Ознайомлення з роботою комп’ютерної програми та явищем інтерференції Ньютона

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.