
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Робоча формула
Розглянемо проходження світла через круглий отвір DD (рис. 68.1). Проведемо з точки О конічні поверхні M1OM1′, M2OM2′, M3OM3′ і т. д. до перетину з поверхнею сферичної хвилі DM0D. Довжини їх виберемо так, що відстань від точок M0, M1, M2, … до точки О збільшується на довжину півхвилі 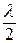 світла, що падає на отвір (
світла, що падає на отвір ( 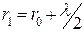 ,
, 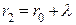 , …,
, …,  ). Утворені конуси поділять поверхню DM0D на сукупність рівновеликих кільцевих зон (зон Френеля).
). Утворені конуси поділять поверхню DM0D на сукупність рівновеликих кільцевих зон (зон Френеля).
 Визначимо висоту сегмента hj. З трикутників SMjC і CMjO маємо
Визначимо висоту сегмента hj. З трикутників SMjC і CMjO маємо
 ,
,
 звідки
звідки
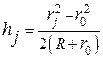 . (68.1)
. (68.1)
Оскільки  , то
, то  . Якщо
. Якщо 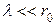 і
і 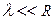 , то членом
, то членом 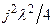 можна знехтувати і тоді
можна знехтувати і тоді 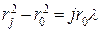 .
.
Підставивши цей вираз у формулу (68.1), одержимо
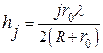 . (68.2)
. (68.2)
Визначимо кількість зон Френеля j, що вміщуються в отворі екрана. З рисунку 68.1 маємо
 .
.
Оскільки  , то величиною
, то величиною  можна знехтувати.
можна знехтувати.
Враховуючи, що 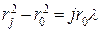 та формулу (68.2), отримаємо
та формулу (68.2), отримаємо
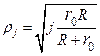 . (68.3)
. (68.3)
Радіус останньої зони Френеля збігається з радіусом отвору, тобто  . Тоді кількість зон Френеля n обчислимо за формулою
. Тоді кількість зон Френеля n обчислимо за формулою
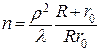 . (68.4)
. (68.4)
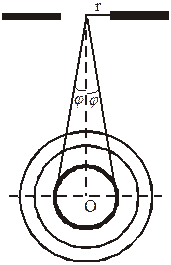 Світлові хвилі від першої і другої зон, дійшовши до точки О, будуть взаємно послаблятися, так що в точці О дія першої зони практично знищується дією другої зони, дія другої зони протилежна до дії третьої зони і т. д. Якщо отвір DD такий, що в ньому вміщується тільки дві зони, то в точці О практично не буде світла (дві сусідні зони взаємно послаблюють одна одну). Отже, ми побачимо на екрані в центрі темний круг, оточений світлим кільцем. Для отвору в якому вкладається три зони Френеля на екрані в центрі буде світлий круг, оточений темним кільцем, за яким знову буде світле кільце. В загальному, за парної кількості зон, в центрі буде темне кільце, оточене почергово світлими і темними кільцями; за непарної кількості зон – у центрі буде світлий круг, почергово оточений темними і світлими кільцями. Чим більший отвір, тим розміри кілець будуть меншими.
Світлові хвилі від першої і другої зон, дійшовши до точки О, будуть взаємно послаблятися, так що в точці О дія першої зони практично знищується дією другої зони, дія другої зони протилежна до дії третьої зони і т. д. Якщо отвір DD такий, що в ньому вміщується тільки дві зони, то в точці О практично не буде світла (дві сусідні зони взаємно послаблюють одна одну). Отже, ми побачимо на екрані в центрі темний круг, оточений світлим кільцем. Для отвору в якому вкладається три зони Френеля на екрані в центрі буде світлий круг, оточений темним кільцем, за яким знову буде світле кільце. В загальному, за парної кількості зон, в центрі буде темне кільце, оточене почергово світлими і темними кільцями; за непарної кількості зон – у центрі буде світлий круг, почергово оточений темними і світлими кільцями. Чим більший отвір, тим розміри кілець будуть меншими.
 Так як розміри зон Френеля залежать від довжини світлової хвилі, то і вигляд дифракційної картини буде залежати від довжини хвилі.
Так як розміри зон Френеля залежать від довжини світлової хвилі, то і вигляд дифракційної картини буде залежати від довжини хвилі.
Для малих кутів дифракції φ (рисунок 68.2) сумарна амплітуда виражається через спеціальну функцію Бесселя 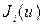 , де
, де 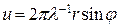 , r–радіус отвору, φ – кут дифракції. Корінь, що відповідає першому мінімуму інтенсивності, тобто визначає кутові розміри центральної світлої плями, визначається з умови
, r–радіус отвору, φ – кут дифракції. Корінь, що відповідає першому мінімуму інтенсивності, тобто визначає кутові розміри центральної світлої плями, визначається з умови
 . (68.5)
. (68.5)
Ця формула відіграє першорядну роль у дифракційній теорії оптичних приладів. Кутові радіуси темних кілець наближено визначаються формулою
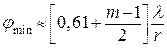 , де m=1, 2, 3, ... (68.6)
, де m=1, 2, 3, ... (68.6)
Лінійні розміри радіуса першого темного кільця приблизно дорівнюють
 . (68.7)
. (68.7)
де L – відстань від отвору до екрана.
Інтерфейс програми
„Дифракція Френеля від круглого отвору“

Зверніть увагу: лінійні розміри дифракційної картини, отриманої на екрані, є в k-разів більшими за справжні розміри.
Завдання 1. Ознайомлення з роботою комп’ютерної програми та явищем дифракції від круглого отвору
Розглянути дифракційну картину отриману з допомогою:
1. Монохроматичного світла;
2. Біхроматичного світла з різною комбінацією двох монохроматичних світлових хвиль, а також з різним міжчастотним інтервалом;
3. Прямокутного спектра з різною його шириною для плоскої поверхні скляної пластини.
Таблиця 68.1 –Варіанти завдань
| Номер варіанту | ||||||||||
| Довжина хвилі, нм |
Читайте також:
- I. Формула спеціальності
- I. Формула спеціальності
- I. Формула спеціальності
- Абсолютні й відносні посилання у формулах
- Барометрическая формула. Распределение
- Барометрична формула
- Барометрична формула. Больцманівський розподіл молекул в
- Барометрична формула. Розподіл Больцмана частинок у зовнішньому потенціальному полі
- Властивості товару „робоча сила”.
- Вступне звернення і заключна формула ввічливості
- Втрати енергії вздовж круглого трубопроводу. Формула Пуазейля і коефіцієнт Дарсі.
- Грування, тобто має місце формула
| <== попередня сторінка | | | наступна сторінка ==> |
| Завдання 3. Визначення довжини хвилі монохроматичного світла | | | Завдання 2. Визначення масштабного коефіцієнта дифракційної картини |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |